Download Formation of current helicity and emerging magnetic flux in solar

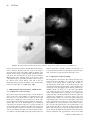
Mon. Not. R. Astron. Soc. 326, 57±66 (2001)
Formation of current helicity and emerging magnetic flux in
solar active regions
Hongqi Zhangw
Beijing Astronomical Observatory, National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012, China
Accepted 2000 November 17. Received 2000 November 1; in original form 2000 June 2
A B S T R AC T
This paper aims to study the properties of the current helicity in solar active regions. The
current helicity provides different information relative to the magnetic helicity and has a
simple relationship with the magnetic energy in the approximation of the force-free field.
For example, we analyse the active region (NOAA 7321) which was a newly emerging delta
active region in 1992 October. It provides good evidence for the development of the magnetic
chirality in the solar active regions. From a series of photospheric-vector magnetograms and
corresponding soft X-ray images, it is found that the newly emerging magnetic flux
associates the current helicity from the subatmosphere in the active regions with the
redistribution of the current helicity density in the upper atmosphere, i.e. it provides
observational evidence that flux and helicity emerge together.
Key words: Sun: magnetic fields.
1
INTRODUCTION
The study of the magnetic (current) helicity in the solar
atmosphere is an important project. It relates to the generation
of the magnetic field from the subatmosphere and the solar
activity on the solar surface. The trans-equatorial sign role of the
magnetic (current) helicity in the solar active regions was
discovered by Seehafer (1990). He found that the most active
regions have negative magnetic (current) helicity in the northern
hemisphere and positive magnetic helicity in the southern
hemisphere. More recently, Martin, Bilimora & Tracada (1993)
showed that in the northern hemisphere most large quiescent
filaments are dextral, while in the southern hemisphere they are
sinistral. The relationship between the electric current helicity in
solar active regions and the solar activity cycle was presented by
Bao & Zhang (1988) and Zhang & Bao (1998).
It is normally believed that the magnetic field forms near the
bottom of the convection zone and emerges at the solar surface
where it forms solar active regions. The observational current
helicity in the active regions, which is inferred by the photospheric-vector magnetograms, probably comes from the emergence of pre-twisted magnetic ropes in the subatmosphere or the
linkage of a different magnetic field, and so on, near the solar
surface. However, until now it has not been very clear whether
magnetic helicity comes up into the solar atmosphere together
with new magnetic flux or whether the flux comes up with no
helicity and gets the helicity later, for instance through the action
of twisting or shearing motion on the already emerged magnetic
field. Thus the study of the magnetic chirality in active regions
w
E-mail: [email protected]
q 2001 RAS
becomes an important project. The photospheric-vector magnetic
field brings some information on the generation of the magnetic
field from the subatmosphere. A possible way to solve this
question is to follow the evolution of the photospheric-vector
magnetic field in the individual active regions, in order to analyse
the possible development of the magnetic shear and the relationship between it and the current helicity, i.e. detailed observations
are needed to decide whether or not the magnetic flux comes pretwisted.
As the total photospheric current helicity density cannot be
inferred by the photospheric-vector magnetograms if one rejects
more assumptions, the different current helicity parameters [such
as Bk ´ …7 B†k and a (introduced from the force-free field) etc.]
have be used to analyse the magnetic chirality in the active
regions. Thus, the comparison between the different current
helicity parameters also becomes important and necessary.
In this paper, we will analyse the formation of the non-potential
magnetic field from a series of photospheric-vector magnetograms
in emerging flux regions. We will compare the photosphericvector magnetic field with the morphological configuration of
solar X-ray images in the analysis of the spatial configuration of
the magnetic field. This is useful in enabling us to understand the
basic properties of the magnetic chirality in active regions. We
will also present the configuration of the electric current helicity
and the relationship it has with the non-potential magnetic field in
active regions.
2
D E F I N I T I O N O F M AG N E T I C H E L I C I T Y
Helicities are topological measures of the structural complexity of
the corresponding fields (Moffatt 1978; Berger & Field 1984;
58
H. Zhang
Figure 1. Two kinds of basic configuration of the magnetic field, corresponding to the linkage (left) and twist (right) of the lines of force in the active regions.
Seehafer 1990). The helicity of magnetic fields may be characterized by several different parameters. The magnetic helicity
density hm ˆ A ´ B, with A the vector potential for magnetic field
B (i.e. B ˆ 7 A†, which measures the chirality of magnetic lines
of force. The total magnetic helicity in a volume V is
…
H m ˆ A ´ B d3 x;
…1†
V
which may not be conserved when finite resistivity is present
(Berger & Field 1984). However, such magnetic helicity cannot be
measured in the solar atmosphere as yet.
The current helicity density hc (where hc ˆ B ´ 7 B† is
another important physical quantity for measuring the magnetic
field in the solar atmosphere. If the magnetic field is not
completely parallel to its vector potential, we can define
7 A ˆ bA ‡ D;
…2†
where D is a perpendicular vector to A. We can then obtain
hc ˆ b2 hm ‡ 7b ´ …A D† ‡ f …D† ´ 7 A:
…3†
…4†
This means that the relationship between the magnetic and current
helicities is complex. We notice that only if 7 A is parallel to A
does the relationship of both helicity densities become simple, and
both helicity densities constantly show the same sign.
According to definition (Berger & Field 1984; Berger 1986),
the magnetic helicity can be separated into two kinds. One is the
self-helicity, which relates to the magnetic flux tubes that are
twisted themselves. This helicity may be used to analyse the
twisted magnetic flux loops. The other is the mutual helicity,
which relates to the different magnetic flux tubes linked to each
other. As the helicity contains both, the total helicity can be
written in the form
2
H m ˆ TF ‡ 2LF1 F2 ;
surface cross-section of the current loop. For a thin, untwisted
current loop, both dl and ds are parallel to the direction of the
electric current, so
B ´ 7 B d3 x ˆ B ´ 7 B dl ´ ds ˆ B ´ dl7 B ´ ds;
so that
where f (D) is a function of the vector D;
f …D† ˆ bD ‡ 7 D:
Figure 2. Two linked, untwisted, closed electric current loops.
…5†
where the T is the twisted number of magnetic flux F and L is the
linkage number of different magnetic fluxes F1 and F2. These
relate to two basic spatial configurations of the magnetic field
systems in the solar active regions, shown in Fig. 1.
The similar case can also be used in the analysis of the current
helicity. Now we consider two thin, untwisted, isolated, linked,
closed current loops (labelled 1 and 2), as shown in Fig. 2; the
electric current is assumed to vanish outside these current loops.
In the case of two linked current loops, the current helicity H c ˆ
H c1 ‡ H c2 : We
„ show that if V completely encloses the two current
loops, H c1 ˆ V B ´ 7 B d3 x provides a measure of their linkage.
The differential element of volume for each current loop is d3 x ˆ
dl ´ ds where dl is an element of length along the loop and ds is the
H c1 ˆ
…6†
‡ …
c1 s1
B ´ dl7 B ´ ds:
…7†
We recall that
„ the current through a surface s is defined as
I ˆ ‰c=…4p†Š
s 7 B ´ ds and can also be expressed as I ˆ
†
‰c=…4p†Š l B ´ dl; where l is the„ contour following the perimeter
of s. The current I 1 ˆ ‰c=…4p†Š s1 7 B ´ ds is invariant along c1.
If we neglect the coefficient c/(4p), we can obtain
…
B ´ dl ˆ I 1 I 2 :
…8†
H c1 ˆ I 1
c1
From symmetry, it is seen that H c2 ˆ I 1 I 2 also. Hence, the current
helicity of two lined, thin, untwisted current loops is
H c ˆ 2I 1 I 2 :
…9†
Similar to equation (5), the general total current helicity can be
written in the form,
H c ˆ TI 2 ‡ 2LI 1 I 2 ;
…10†
where I, I1 and I2 are the electric current systems.
3 O B S E RVAT I O N A L E V I D E N C E O F T H E
M AG N E T I C C H I R A L I T Y
Although the determination of the real total current helicity is a
complex problem in the solar atmosphere, the marks of the current
helicity in the photosphere can be detected by the photosphericvector magnetograms. We can analyse the distribution of the
current helicity density and its evolution in the photosphere.
q 2001 RAS, MNRAS 326, 57±66
Current helicity in solar active regions
Oct. 25, 01:07
Oct. 25, 05:41
Oct. 26, 01:38
Oct. 27, 02:53
59
Figure 3. Vector magnetograms resolved in the 1808 ambiguity of transverse fields in the active region (NOAA 7321) observed on 1992 October 25±27. The
solid (dashed) contours correspond to positive (negative) fields of ^50, 200, 1000, 1800, 3000 Gauss. North is at the top and east is at the left of the diagram.
3.1
Evolution of the photospheric magnetic field
For the analysis of the development of the magnetic chirality, as
an example, we firstly illustrate the emergence of magnetic flux
forming a new active region (NOAA 7321) from 1992 October 25
to November 1, observed at the Huairou Solar Observing Station
at Beijing Astronomical Observatory. The preliminary analysis on
the relationship between the emerging magnetic flux and the
electric current in this region was made by Zhang (1995).
This emerging flux region (EFR) was born on 1992 October 23
and gradually formed a new delta active region (NOAA 7321). In
Fig. 3, we show the vector magnetograms resolved for a 1808
ambiguity of the transverse field in AR 7321 on 1992 October 25±
27. The tilt angle of the magnetic axis of the main poles of this
active region relative to the solar equator is about 608. The
magnetic flux of this active region emerged rapidly, as the main
poles of opposite polarity moved away at a speed of about
0.4 km s21 on 1992 October 25. The transverse components of the
magnetic field gradually became parallel to the magnetic neutral
line in the middle of the active region. On October 26 and 27, the
shear of the transverse field increased near the magnetic neutral
line and the total flux of the longitudinal field also increased. We
also notice that in the northern side of the magnetic main pole of
negative polarity and in the southern side of the magnetic main
q 2001 RAS, MNRAS 326, 57±66
pole of positive polarity, the transverse magnetic field extends out
and almost keeps the basic configuration of the potential field.
Amounts of magnetic flux emerged mainly near the magnetic
neutral line between the magnetic main poles (S and N) of opposite
polarities (Zhang 1995). A similar case was demonstrated by Zhang
& Song (1992). The magnetic shear in the emerging flux region is
normally caused by the emergence of the small-scale magnetic flux
of opposite polarity. The two-dimensional singular points of the
magnetic field, inferred by the photospheric-vector magnetograms
on October 27 in the active region, were analysed by Wang, Wang &
Qiu (1999). The magnetic connectivity of the transverse field
provides the vestige of the topology of the magnetic lines of force in
(or above) the photosphere. These provide a basic morphology of the
formation of the twisted magnetic field in the active region.>
3.2 Current helicity parameters Bk ´ …7 B†k and a
We notice that the current helicity density can be written as the
sum of two parts:
hc ˆ Bk ´ …7 B†k ‡ B' ´ …7 B†' :
…11†
The first term on the right-hand side of equation (11) is
observable, and can be inferred by photospheric-vector magnetograms (Abramenko, Wang & Yurchishin 1996). However, the
60
H. Zhang
Oct. 25, 01:07
Oct. 25, 05:41
Oct. 26, 01:38
Oct. 27, 02:53
Figure 4. The electric current helicity parameter Bk ´ …7 B†k in the active region (NOAA 7321) during 1992 October 25±27, and the size of the maps is the
same as Fig. 3. The solid (dashed) contours indicate the positive (negative) regions of the current helicity distribution of ^0.0025, 0.01, 0.025, 0.05, 0.09,
0.15 G2 m21. The arrows mark the transverse magnetic field.
second term is difficult to obtain as one rejects more assumptions,
because no observational data of the vector magnetic field in the
other layers of the solar atmosphere is available.
If one neglects the second term (the combined one between the
transverse magnetic field and transverse current in the current
helicity) on the right-hand side of equation (11), one can analyse
the chirality of the magnetic field near the areas where the
longitudinal component of the magnetic field and electric current
are more dominant than the transverse ones. It is important to
provide the basic property of the twisted magnetic field near
strong magnetic poles in the active regions, because one normally
believes that the magnetic poles extend vertically upwards from
the deep atmosphere (Lites & Skumanish 1990). The observational part of the current helicity density is
hc…obs† ˆ Bk ´ …7 B†k ˆ Bz
­By ­Bx
2
:
­x
­y
…12†
The derivatives are approximated by a four-point differencing
scheme; the current helicity is computed at each intersection of
four magnetogram pixels and the calculated helicity is smoothed
to eliminate the small-scale fluctuation of the observed data
(Wang, Xu & Zhang 1994).
Fig. 4 shows the distribution of the current helicity parameter
Bk ´ …7 B†k inferred by the vector magnetic field in the active
region (NOAA 7321). If it is compared with the distribution of the
corresponding magnetogram, we can find that the opposite signs
of the current helicity exist in the same main magnetic poles in the
active region, and the sign of the current helicity does not change.
The intensity of the current helicity parameter Bk ´ …7 B†k in the
solar photosphere increased over the period October 25±27. The
mean intensities of the current helicity parameter Bk ´ …7 B†k for
the areas of Bk . 250 G in Fig. 4 at 01:07 and 05:41 ut on
October 25, 01:28 ut on October 26 and 02:53 ut on October 27
are 2.6, 4.7, 8.5 and 7.2 respectively (the unit is 1022 G2 m21). We
can infer that the helicity in most areas of the active region is
positive. This means that the current helicity density increases in
the photosphere with the emerging magnetic flux in the active
region. On 1992 October 27, the total intensity of the current
helicity parameter Bk ´ …7 B†k in the photosphere was 5:3 1010 G2 m (in unit height) and was larger than the normal active
regions (Zhang & Bao 1998).
From letting B ˆ Bb; where b is a unit vector along the
direction of the magnetic field, the current helicity density may be
written in the form (Zhang & Bao 1999)
hc ˆ aB2 ;
…13†
q 2001 RAS, MNRAS 326, 57±66
Current helicity in solar active regions
Oct. 25, 01:07
Oct. 25, 05:41
Oct. 26, 01:38
Oct. 27, 02:53
61
Figure 5. The a -factor of the force-free field in the areas where the longitudinal field is larger than 250 G in the active region (NOAA 7321) during 1992
October 25±27; the size of the maps is the same as Fig. 3. The solid (dashed) contours indicate the positive (negative) a -factor distribution of ^0.25, 1.0, 2.5,
5., 10.0, 15.0 (1027M21). The others are the same as Fig. 4.
where
a ˆ b ´ 7 b:
…14†
The term a is a factor reflecting the helicity of the unit magnetic
field. In the approximation of the force-free field, the a -factor can
be obtained by the formula
…7 B†k ´ Bk
­By ­Bx
2
=Bz :
aˆ
ˆ
…15†
­x
­y
B2k
We display the a -factor in the areas where the longitudinal
magnetic field is larger than 250 G, in the active region NOAA
7321, shown in Fig. 5. Even through, the most information of the
a -factor in the active region can be found. This approximation can
probably be used to analyse the photospheric strong magnetic field
in active regions (Canfield et al. 1993), but has failed in some of
areas in the active region because the gas pressure is not negligible
relative to the magnetic pressure (Zhang 1997). If the deviation
from the force-free field is not obvious in the active regions, it can
be used to analyse the distribution of the photospheric magnetic
helicity density. The current helicity density in the photosphere
inferred by equation (13) has the same sign distribution with a in
the approximation of the force-free field. The mean current
helicity densities (a B2) for the areas of Bk . 250 G at 01:07 and
q 2001 RAS, MNRAS 326, 57±66
05:41 ut on October 25, 01:28 ut on October 26 and 02:53 ut on
October 27 in the active region NOAA 7321 are 3.1, 6.7, 15.6 and
14.4 respectively (the unit is 1022 G2 m21). The current helicity
density hc ˆ aB2 shows a similar tendency to increase with Bk ´
…7 B†k : On the other hand, as we pay attention to the a -factor of
the active region in the photosphere, we can find that the density
of the a -factor did not change significantly on October 26 and 27.
Wang & Wang (1998) found that in the active region NOAA 7321
the a -factor tends to retain its sign and a slow growth speed. The
mean a values for the areas of Bk . 250 G at 01:07 and 05:41 ut
on October 25, 01:28 ut on October 26 and 02:53 ut on October
27 in Fig. 5 are 3.2, 5.6, 6.6 and 7.0 respectively (the unit is
1028 m21). This means that in the emergence of new magnetic
flux in the active region the degree of twisting in the magnetic
lines of force does not change significantly, except in the initial
stage of the magnetic shear in the active region on October 25.
As we compare the distribution of the a -factor with Bk ´ …7 B†k
in the photosphere, we find that both the parameters also show the
same sign distribution, but the a -factor brings more information
on the highly sheared magnetic field (such as near the magnetic
neutral line) and also no real information on B' ´ …7 B†' : The
resolution of the 1808 ambiguity of the highly sheared
transverse magnetic field normally is difficult in areas near the
magnetic neutral lines in the flare-producing active regions. The
62
H. Zhang
Figure 6. The sunspot (left) and soft X-ray (right) images on October 26 (top) and 27 (bottom) in the active region NOAA 7321.
magneto-optical effect is another notable problem for the measurement of transverse magnetic field near centre of the sunspots
where the field is strong and with the smaller inclination of the
magnetic field to the line of sight (Landolfi & Landi Degl'Innocenti 1982). The observational error (about 108 for the Huairou
Magnetograph) of the azimuthal angles of the transverse field,
caused by the magneto-optical effect, probably causes a change of
the observed mean current helicity value, but it does not
significantly change the basic information of the current helicity
in the active region (Bao et al. 2000; Zhang 2000).
4
4.1
F O R M AT I O N O F M AG N E T I C C H I R A L I T Y
Configuration of soft X-ray images
Fig. 6 shows sunspot and soft X-ray images on 1992 October 26
and 27 in the active region NOAA 7321 obtained by the Soft
X-ray Telescope on board the Yohkoh satellite. It can be found
that the basic configuration of the soft X-ray loops in the active
region changed significantly. If compared with the vector magnetograms in Fig. 3, we can see that the bright loops on October 26
correspond to the magnetic main poles of opposite polarities. It
can be inferred that the magnetic field likes the potential one
above the photosphere. However, on October 27, the configuration
of the loops is different from that on October 26 and shows more
of a tendency towards the highly sheared photospheric transverse
magnetic field. This is probably caused by the emergence of a
non-potential field from the lower atmosphere and the rearrangement of the basic topological magnetic field in the corona.
4.2
Configuration of magnetic chirality
The development of the magnetic shear with the emerging active
region was discussed by Wang et al. (1994). If we compare the
evolution of the current helicity parameter Bk ´ …7 B†k on
the different days shown in Fig. 4, the significant change of the
current helicity density in the photosphere can be found. The mean
growing-rate of the photospheric current helicity parameter Bk ´
…7 B†k is about 1:5 105 G2 m s21 in the active region NOAA
7321, during the period 1992 October 24±27. The force-free
model of the magnetic field is a powerful tool for analysing the
spatial static state of the magnetic field above the photosphere. By
comparing the configuration of soft X-ray images from 1992
October 26 and 27 in Fig. 6, we can show the spatial configuration
of the magnetic lines of force above the photosphere extrapolated
by the approximation of the linear force-free field in the active
region NOAA 7321 in the top and side-on view (see Figs 7 and 8).
We can see that the approximation of the potential field …a ˆ 0†
from October 26 in Fig. 7 is basically consistent with the distribution of the soft X-ray loops above the photosphere in the active
region, although the highly sheared magnetic field forms near the
magnetic neutral line. The approximation of the force-free field
q 2001 RAS, MNRAS 326, 57±66
Current helicity in solar active regions
‰a ˆ 0:45 …unit ˆ 10 1000 km†Š observed on October 27 is used in
Fig. 8. The distributions of the magnetic lines of force in both days
are roughly consistent with that of the soft X-ray loops in the
active region. It is evident that the formation of the large-scale
sheared magnetic field is delayed more in the corona than that in
the photosphere. The emerging magnetic flux changes the preexisting potential-like configuration of the magnetic field to the
non-potential one in the active region.
As we study the variation of the current helicity by using
63
Faraday's law …­B†=…­t† ˆ 2c7 E, the evolution of the current
helicity density can be derived;
­hc
ˆ 22c7 E ´ 7 B 2 c7 ´ ‰…7 E† BŠ:
­t
…16†
This shows a similar form to the magnetic helicity density
obtained by Berger & Field (1984),
­hm
ˆ 22cE ´ B 2 c7 ´ …E A ‡ fB†;
­t
…17†
Figure 7. The distribution of the magnetic lines of force above the photosphere on 1992 October 26 in the active region NOAA 7321 in (top) the top and
(bottom) the side-on views. The short bars and thick dashed lines mark the photospheric transverse magnetic field and magnetic neutral lines respectively.
q 2001 RAS, MNRAS 326, 57±66
64
H. Zhang
where f is the scalar potential. As the volume V is fixed, one can
integrate equation (16) over V, where S is the surface of V, to find
that
‡
…
dH c
ˆ 22c …7 E† ´ …7 B† d3 x 2 c ‰…7 E† BŠ ´ dS:
dt
V
S
…18†
It is found that the current helicity is not conserved. If the ideal
Ohm's law applies, then E ˆ 2‰…1/c†=…V B†Š: We can find that
the time variation of the current helicity depends on the twisted
motion
and variation of the magnetic field. From the second term
„
{ S ‰7 …V B† BŠ ´ dS} in equation (18), it is found that the
emergence of sheared magnetic flux in the solar surface actually
reflects the transport of the current helicity density from the
interface, such as the solar photosphere or subatmosphere.
Moreover, the equivalent evolution of the electric current helicity
also can be described by the form of the electric current systems in
the solar atmosphere in equation (10). By comparing this with
equations (2)±(4), one can probably obtain the conclusions that
the similar conservation property of the current helicity relative to
the magnetic helicity can be restricted in the approximation of the
linear force-free field and that a stays constant.
In the approximation of the force-free magnetic field in
equation (13), we find that the change of the current helicity
density obviously relates to that of the force-free factor and the
magnetic energy density. The ratio between the current helicity
Figure 8. The distribution of the magnetic lines of force above the photosphere on 1992 October 27 in the active region NOAA 7321 in (a) the top and (b) the
side-on views. The short bars and thick dashed lines mark the photospheric transverse magnetic field and magnetic neutral lines respectively.
q 2001 RAS, MNRAS 326, 57±66
Current helicity in solar active regions
65
Figure 9. The topological change of the magnetic field above the photosphere in the active region on 1992 October 26 (left) and 27 (right) in the top (top) and
side-on (bottom panel) views in the active region. The dashed lines mark the magnetic lines of force before the reconnection of the field. The thick arrow
shows the moving direction of the emerging magnetic flux.
and magnetic energy can be written in the form
„
„
2 3
B ´ 7 B d3 x
Hc
v
v aB d x
„
Rˆ
ˆ „
ˆ
8p
ˆ 8pa ;
2
2 3
3
Wm
v …B =8p† d x
vB d x
…19†
where aÅ is the mean force-free factor. If the magnetic field in the
active region does not significantly change, we can analyse the
evolution of the current helicity density in the photosphere by that
of the a -factor only (Pevtsov, Canfield & Metchalf 1994).
However, the change of the magnetic field intensity is an
important index in most of the active regions, such as emerging
flux regions. This means that we also need information on the
magnetic field to analyse the development of the photospheric
current helicity density in the active region. From the above
analysis of the photospheric-vector magnetograms and the corresponding current helicity in the active region NOAA 7321, the
possible formation model of the photospheric current helicity
shows the combination between the emergence of magnetic-flux
arranged abnormal polarities and pre-existing magnetic field in the
active region.
The study of the magnetic helicity is a complex problem,
because one can only obtain
hm ˆ
B2
a
…20†
in the approximation of the linear force-free field (Pevtsov,
Canfield & Metchalf 1995), where B and a are observable in the
photosphere. It is found that the magnetic helicity density has
the same sign distribution as a , but normally one cannot obtain
the simple conclusion that the mean magnetic helicity density
has the same sign as the mean a -value on the solar surface,
because the weak a -areas, which may have the opposite sign to
the mean a -value, have been amplified in the calculation. This
means that the observational study of the magnetic helicity in the
solar atmosphere is much more difficult than the study of the
current helicity, even in the photosphere.
During the development of the new active region (NOAA
q 2001 RAS, MNRAS 326, 57±66
7321), some flares occurred near the highly sheared magnetic
neutral line in the active region (Zhang 1995; Liu et al. 1998;
Wang et al. 1998). Liu et al. (1998) provided a good consistence
between the extrapolated photospheric magnetic field in the high
solar atmosphere in the approximation of the force-free field
model and the distribution of the soft X-ray loops observed on
1992 October 27. On 1992 November 2, the large, soft X-ray
flare-loops were observed from the side-on point of view as the
active region rotated near the western solar limb (Ichimoto et al.
1993), and it can be inferred that footpoints of the cusp flareloops observed on November 2 were located at the magnetic
main poles of opposite polarity in the active region (Sakurai
1994). It is evident that a large amount of emerging magnetic
lines of force significantly change the configuration of the
magnetic field above the photosphere, which triggers the
reconnection of the large-scale magnetic field (i.e. the flares).
A possible change of the magnetic field, caused by the emerging
magnetic flux near the middle of active region, is shown in
Fig. 9. One believes that the morphology of soft X-ray images
reflects the configuration of the magnetic field in Fig. 6 and
considers the curvature of the magnetic lines extrapolated by the
force-free field in Figs 7 and 8. The rough conservation of
the magnetic helicity probably exists in the rapidly reconnected
process of the magnetic field above the photosphere (Berger &
Field 1984) and the topology of the magnetic field changes to a
relatively simple form. It is noticed that the approximation of the
force-free field normally is correct in the solar corona. This
means that in the upper atmosphere, the electric current is
roughly parallel to the magnetic lines of force. The topological
change of magnetic lines of force in the solar corona
probably reflects the electric current change and gives some
information on the current helicity. However, this approximation
probably does not always hold in the lower solar atmosphere.
The change of the current helicity density in the photosphere
during solar flares was demonstrated by Bao et al. (1999), which
provides a real trace of the change of current helicity above the
photosphere.
66
H. Zhang
REFERENCES
Bao S. D., Pevtsov A. A., Wang T. J., Zhang H. Q., 2000, Sol. Phys., 195,
75
Berger M. A., Field G. B., 1984, J. Fluid Mech., 147, 133
Berger M. A., 1986, Geophys. Astrophys. Fluid Dyn., 34, 265
Canfield R. C. et al., 1993, ApJ, 411, 362
Ichimoto K. et al., 1993, in Sakurai T., Hirayama T., Ai G., Proc. II Japan±
China Seminar on Solar Physics, NAOJ, 151
Landolfi M., Landi Degl'Innocenti E., 1982, Sol. Phys., 78, 355
Lites B. W., Skumanich A., 1990, ApJ, 348, 747
Liu Y., Akioka M., Yan Y. H., Ai G. X., 1998, Sol. Phys., 177, 395
Martin S. f., Bilimora R., Tracada P. W., 1993, BAAS, 25, (3), 1217
Moffatt H. K., 1978, Magnetic Field Generation in Electrically Conducting
Fluids. Cambridge Univ. Press, Cambridge
Pevtsov A. A., Canfield R. C., Metchalf T. R., 1994, ApJ, 425, L117
Pevtsov A. A., Canfield R. C., Metchalf T. R., 1995, ApJ, 440, L109
Sakurai T., 1994, in Enome S., Hirayama T., eds, Proc. Kofu Symp., New
Look at the Sun with Emphasis on Advanced Observations of Coronal
Dynamics and Flares, NRO Report No. 360, NAOJ, 363
Seehafer N., 1990, Sol. Phys., 125, 219
Wang T. J., Xu A. A., Zhang H. Q., 1994, Sol. Phys., 155, 9
Wang T. J., Qiu J., Zhang H. Q., 1998, A&A, 336, 359
Wang T. J., Wang H. N., 1998, Astrophys. Rep. Special Issue, No. 4,
Beijing Astron. Obs., Beijing, p. 62
Wang T. J., Wang H. N., Qiu J., 1999, A&A, 342, 854
Zhang H. Q., 1995, A&A, 304, 541
Zhang H. Q., 1997, A&A, 324, 713
Zhang H. Q., 2000, Sol. Phys., 197, 235
Zhang H. Q., Song M. T., 1992, Sol. Phys., 138, 69
Zhang H. Q., Bao S. D., 1998, A&A, 339, 880
Zhang H. Q., Bao S. D., 1999, ApJ, 519, 876
Abramenko V. I., Wang T. J., Yurchishin V. B., 1996, Sol. Phys., 168, 75
Bao S. D., Zhang H. Q., 1998, ApJ, 496, L43
Bao S. D., Zhang H. Q., Ai G. X., Zhang M., 1999, A&AS, 139, 311
This paper has been typeset from a TEX/LATEX file prepared by the author.
5
R E S U LT S
After the analysis, the main results are as follows.
(i) The current helicity is observable in the solar atmosphere. It
is not conservative and probably changes with the evolution of the
magnetic field. The relationship between the current helicity and
magnetic helicity is usually complex. The current helicity shows a
relatively simple relationship with the a -factor and the magnetic
energy in the approximation of the force-free field.
(ii) The formation of the current helicity of the active region in
the solar surface is connected with the newly emerging magnetic
flux. The increase of the helicity density around the main
magnetic poles is continuously contributed to by a series of
emerging flux with opposite polarity arrangement. This means
that the topological change of the current chirality in the solar
surface is probably brought up from the sub-atmosphere.
AC K N O W L E D G M E N T S
HZ is grateful to staff at Huairou Solar Observing Station for their
support in these observations. This research was supported by the
Chinese Academy of Sciences and the National Science Foundation of China.
q 2001 RAS, MNRAS 326, 57±66