Download get Assignment File

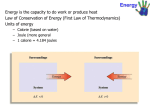
What do you already know about
energy?
Energy needs in the natural
world?
Comes from the sun
 Chemical bonds of photosynthesis
 Chemical bonds of cellular respiration
 Energy for life
 Heats the atmosphere – controls climate

Why is Energy Important?
Energy for human advancement and sustenance

Fossil fuels
 Worth war?
 Extraction processes? Kinds of costs?
 Worth the waste?
○ Implications for earth as a whole?
Alternative energy sources to
Fossil Fuel
Practical?
 Universal?
 Why hasn’t it already happened?

What is Energy?

The capacity to do work OR produce heat
Law of Conservation of Energy
Energy can be converted from one form to
another but can be neither created nor destroyed
 Energy of the Universe is CONSTANT

Potential Energy

Energy due to position or
COMPOSITION (chemical bonds)
 Position: water behind a dam
converts eventually to electrical
energy
 Composition: Gasoline burns to
release energy (due to attractive
and repulsive forces in the
reactants and products of
combustion)
Kinetic Energy

Energy of an object is due to the motion of the
object
 Depends on the mass (m)
 Depends on its velocity (v)
 KE = 1/2mv2
Energy can be transferred orHow is PE
converted to
Converted
KE?
Are there
other forces?
Is any energy
lost?
If so, where
did it go?
Is there any
frictional
heating
happening?
What is the difference between heat
and temperature?
Temperature – measures the random motions of
the particles in a substance
 Heat – TRANSFER of energy between TWO
objects due to temperature differences. (heat is
NOT contained in an object!!)

Heat versus Temperature
What is WORK??

Work is defined as force acting over a
distance
Is any work
happening?
There are TWO ways energy can
be transferred!
By WORK
 By HEAT

The way energy is divided between work
and heat depends on Pathway
1. If pathway is ROUGH, maybe NO
work is done, but a lot of heat is
generated
2. If pathway is SMOOTH, a lot of
work can be performed, maybe with little
What is a State Function/Property?

SF/P – any property that only depends on
its PRESENT state.
 Value doesn’t depend on how the system
arrived.
 Change in SF/P is independent of the pathway
 Analogy: Imagine a trip from Chicago to Denver
○ Consider elevation. No matter how you travel the
elevation change is the same (state function)
○ Consider distance. Distance totally depends on
the pathway you take (not a state function)
Are either of these pathways a state function?
Compare System and Surroundings
System – is place of focus (example: calorimeter)
 Surroundings – anyplace outside the system
(outside the calorimeter)

Two heat possibilities in reactions
Exothermic – heat is REMOVED from
the system
 Endothermic- heat is added to the
system

Where does heat come from in exothermic
reactions?
Difference in potential energies between the
products and the reactions.
 If reactant has higher potential energy than
reactant – heat will be given off from the system
 Energy gained by the surrounding must be equal
to the energy lost by the system

Example of exothermic event

CH4 + 2 O2  CO2 + 2H2O +
(energy)heat
 CH4 + 2O2 have MORE potential energy in
the chemical bonds than CO2 + 2H2O
have in their bonds
 Heat flow results from lowering the potential
energy
 All exothermic reactions result in thermal
energy release via heat
ExoThermic Heat flow diagram:
Endothermic
Energy flows INTO the system
 Products have more energy (PE) than
reactants

Endothermic Heat Flow
Thermodynamics

Study of energy and its interconversions
First Law of Thermodynamics

The energy of the universe is constant
Internal Energy (E)
Sum of the KE + PE of all “particles” of
the system
 E can be changed by a flow of work,
heat or both

∆E=q+w
○ ∆ E= internal energy
○ Q = heat
○ W = work
What does this Flow chart
mean??
The lines
represent exo
and endo
thermic
reactions.
Which color is
which?
Thermodynamics symbology

TWO numbers
 Magnitude = quantity
 Sign= perspective
○ OURS – from the system point of view
 Exothermic = negative sign (energy LEAVES
the system)
 Endothermic = + sign (energy is GAINED by
the system)
 Same conventions for work
○ Engineers - reversed
Now problem pg 233- Sample problem 6.1
Sample Exercise 6.1 (p. 233): Calculate ΔE for a
system undergoing an endothermic process in
which 15.6 kJ of heat flows and where 1.4 kJ of
work is done on the system.
We write the magnitudes and signs of the heat and
the work as:
q = +15.6 kJ
and
w = +1.4 kJ
Both signs are positive because heat flows into the
system and work is performed on the system. We then
plug these quantities into the First Law (∆ E = q + w)
to obtain the answer:
ΔE = +15.6 kJ +1.4 kJ = 17.0 kJ
The system has gained energy, so ΔE is a positive
quantity. This is consistent with the fact that the
process is endothermic.
Work of GAS Expansion and Compression

Example pistons move due to expansion of gas
(work is done)
Work of GAS Expansion and Compression

The pressure (P) of the gases is related to the force (F)
and the area (A) of the piston by the following equation:
P = F/A


We can solve this for the force; it is simply: F = P∙A
Work is defined as force exerted over a distance. In this
case, the distance is represented as Δh, so we can
write the work as:
work = F∙Δh

Substituting for the force, we obtain:
work = P∙A∙Δh = P∙ΔV

Here ΔV is the difference between the final volume and
the initial volume. What is the sign of this work?
In this case, our system is expanding its volume against
the surroundings, hence it is performing work on the
surroundings. Thus the sign of the work should be
negative, even though P and ΔV are both positive
quantities. This forces us to write:
w = — P∙ΔV
More details p. 233
for the work done against the surroundings by an
expanding gas. Note that this same expression gives
us the correct sign in the case of the surroundings
doing work on the system to compress a gas. In this
case, ΔV is a negative quantity, making w a positive
quantity.
Sample Exercise 6.2 (p. 234):

Calculate the work associated with the
expansion of a gas from 46 L to 64 L at a
constant external pressure of 15 atm.

 We start with our expression for work:
w = — P∙ΔV
Since ΔV is given by:
ΔV = Vfinal — Vinitial
 We obtain for w:
w = — P∙( Vfinal — Vinitial) = —15∙(64 — 46) L∙atm
= —270 L∙atm
The negative sign on this result is consistent with the fact
that the system does work on the surroundings by its
expansion.
Sample Exercise 6.3

A balloon is being inflated by heating the air inside it. In the final states
of the process, the volume of the balloon expands from 4.00x106 L to
4.50x106 L through the addition of 1.3x108 J of energy to the balloon in
the form of heat. Assume that the external pressure remains at a
constant 1.0 atm. Calculate ΔE for the process. To convert between J
and L● atm, use 1 L ● atm = 101.3 J

We will start with the First Law:
ΔE = q + w

Since 1.3x108 J of energy was added as heat, we can write that:
q = +1.3x108 J
And we can calculate the work:
w = — P∙ΔV = — (1.0 atm)∙(0.50x106 L) = — 0.50x106 L∙atm
 The sign is negative, since the gas is expanding and doing work on the
surroundings.

Now we want to convert the work from L∙atm to J. We can use the unit factor:
(101.3 J)=(1 L∙● atm)
Thus the work is:
w = — (0.50x106 L∙atm)∙(101.3 J)/(1 L∙atm) = — 0.51x108 J
Now we are ready to plug the work and the heat into the First Law:
ΔE = +1.3x108 J — 0.51x108 J = +0.8x108 J
Enthalpy









The Enthalpy (H) of a system is defined in terms of the internal energy (E), pressure
(P) and volume (V) of the system:
H = E + PV
Since internal energy, pressure, and volume are all state functions, enthalpy is also
a state function. But what is enthalpy?
Consider a process carried out at constant pressure and such that the only work is
pressure-volume work. (w = — P∙ΔV for pressure-volume work.) If we define qP as
the heat of a process run at constant pressure, we can write the First Law:
ΔE = qP + w = qP — P∙ΔV
Solving for qP we obtain:
qP = ΔE + PΔV
Now we can relate qP to a change in enthalpy. Since we defined enthalpy as: H = E
+ PV
We can write a change in enthalpy (ΔH) as:
ΔH = ΔE + Δ(PV)
Since our process runs at constant pressure, we can rewrite this as:
ΔH = ΔE + PΔV
But this is the same as our earlier expression for qP, the heat of a process run at
constant pressure such that the only work is PV work. Thus:
ΔH = qP
Thus at constant pressure (and where only PV work is allowed), the change in
enthalpy (ΔH) of the system is equal to the energy flow as heat. Because of this
equality, we can say that in a reaction run at constant pressure, the change in
enthalpy is the same as the heat of the reaction.
Sample Exercise 6.4 (p. 236):
Sample Exercise 6.4 (p. 236): When 1 mole of
methane (CH4) is burned at constant pressure,
890 kJ of energy is released as heat. Calculate ΔH
for a process in which 5.8 g of methane is burned
at constant pressure:
 We can write the heat of reaction (at constant
pressure) as:

qp = ΔH = -890 kj/mol CH4
 Since the number of moles of methane is:.36 mol
 The heat of the process where 5.8 g of methane
burns at constant pressure thus is:
.36 mol CH4 x -890kj/mol = -320kj
Calorimetry
Calorimetry is an experimental process for
measuring heats of reaction.
 calorimeter. The device used for measuring heats
of reactions

Heat Measurements, Temperature, and Heat
Capacity

We do not have a way to make direct
measurements of heat. What we actually measure
is temperature, or, more specifically, the change in
temperature resulting from a chemical reaction.
Through knowledge of the heat capacity of the
substance containing the heat generated by the
process. We define the heat capacity (C) of a
substance as:
C = heat absorbed/ increase in temperature
Influence of the heat capacity of water:
Units of Heat Capacity

If we heat a substance, the rise in temperature we obtain
from adding a particular amount of heat depends on the
amount of substance that is present.
 Specific Heat Capacity: When we express a heat
capacity in terms of the mass of substance that is
heated, we use units of joules per C° per gram, or
equivalently, joules per Kelvin per gram per Kelvin
(J/K∙g). Some specific heat capacities are given in Table
6.1:
•Molar Heat Capacity: When we
express a heat capacity in terms of
the number of moles of substance
that is heated, we use units of joules
per C° per mole, or equivalently,
joules per Kelvin per mole (J/K∙mol).
Constant Pressure Calorimetry:

Constant pressure calorimetry is
nothing more than calorimetry
carried out under conditions of
constant pressure. A simple
device for doing calorimetric
measurements at ambient
pressure is illustrated in Figure
6.5. It is made from Styrofoam
coffee cups (hence the name,
coffee cup calorimeter), but it is
accurate enough for a student
to use in chemistry lab
Constant Pressure Calorimetry:








Used for reactions in aqueous solutions. (Recall: heat generated in an exothermic reaction run at constant
pressure is the change in enthalpy of the system.)
We’ll follow the example in the text on pages 237-9, where we take 50.0 mL of 1.0 M HCl at 25.0 °C and 50.0
mL of 1.0 M NaOH also at 25.0 °C and mix them in the calorimeter. After we stir the mixed solutions, we
measure a temperature of 31.9 °C. From these data we wish to determine the heat of the reaction that has
just taken place inside the calorimeter.
The reaction is the neutralization of a strong acid by a strong base:
H+ (aq) + OH— (aq) ——> H2O (l) + qP
Since we observed an increase in temperature, we know that the reaction generated heat, and we include
this heat (qP) on the right hand side.
At this point you might argue that the heat still remains in the system; that it has yet to flow to the
surroundings. We can answer this argument two ways (They both yield the same result.):
1) We can define the system as consisting only of the ions that have reacted and the small amount of
water that they generated in the reaction. Then the surroundings include the solvent water, and
essentially all the heat produced by the reaction now resides in that portion of the surroundings that is
inside the calorimeter.
2) Alternatively we could argue that the system includes the solvent, and the surroundings stop at the
inside wall of the calorimeter. The heat that produced the rise in temperature has been temporarily
captured within the system, and we can measure it before it flows out of the system into the
surroundings.
Either way, the heat of the reaction was sufficient to raise the temperature of 100.0 mL of water by 6.9
Kelvins. But how much heat is this? If we consult Table 6.1, we see that the heat capacity of water (Cwater) is
4.18 J/K∙g. Thus:
q = Cwater ∙ m water ∙ ΔT = (418 J/K ∙ g) (100.0 g) (6.9K) = 2.9 x 103
Here q is the heat actually produced inside the calorimeter by the reaction of the HCl (aq) with the NaOH
(aq). (We have assumed that the volume of the solution is exactly the combined volumes of the HCl (aq) and
the NaOH (aq) and that the density of the solution is exactly 1.000 g/mL.) What if we had reacted twice as
much acid with twice as much base? We would have obtained twice as much heat. What if we had reacted
1.00 mole of HCl (aq) with 1.00 mole of NaOH (aq)? We can calculate this from the number of moles that
actually reacted and the heat (q) that was produced:
H HCl = VHCl MHCl = (0.0500 L) (1.0 mol/L) = .050 mol
ΔH = -q/nHCl = -2.9 x 103 J/.050mol = 58kJ/mol
Here ΔH represents the enthalpy of reaction for 1 mole of HCl (aq) reacting with 1.00 mole of NaOH (aq).
Sample 6.5 pg. 239


1.00 L of 1.00 M Ba(NO3)2 solution at 25.0 °C is reacted with 1.00 L of 1.00
M Na2SO4 solution, also at 25.0 °C in a constant pressure calorimeter. A
white, solid precipitate of BaSO4 forms and the temperature of the mixture
rises to 28.1 °C. Calculate the enthalpy change per mole of BaSO4 that
forms. You may assume that the calorimeter absorbs a negligible amount of
heat, that the specific heat capacity of the solution is 4.18 J/K∙g, and that
the density of the solution is 1.0 g/mL.
First we write the net ionic reaction:
Ba2+ (aq) + SO42— (aq) ——> BaSO4 (s)
We observed a rise in temperature, indicating that the reaction generated
heat. Thus the reaction is exothermic and the change in enthalpy (ΔH)
will be negative. The volume of the combined solution is 2.00x103 mL, so
the mass of the solution is 2.00x103 g. The change in temperature is 3.1
K. Thus the heat evolved by the reaction is:

q = Cwater ∙ m water ∙ ΔT = (4.18 J/K∙ g) (2.00 x 103 g) (3.1 K) = 2.5 x 104 J
Since the reaction produced 1 mole of BaSO4 (s), the molar enthalpy
change is
ΔH = -q = -2.6 x 104 J/mol = -26kj/mol
Bomb Calorimeter
You are not required to do
problems associated with
this type of calorimeter, but
it is cool to contemplate!
Hess’s Law
 law
used to predict the enthalpy change and
conservation of energy (denoted as state
function ΔH) regardless of the path through
which, it is to be determined. The law states
that because enthalpy is a state function, the
enthalpy change of a reaction is the same
regardless of what pathway is taken to
achieve the products. In other words, only the
start and end states matter to the reaction, not
the individual steps between.
Hess’s Law Example:(see schematic next slide)

Example 1. The oxidation of nitrogen to produce
nitrogen dioxide. The enthalpy change ΔH of the
reaction is 68 kJ
N2(g) + 2O2(g) = 2NO2(g)
ΔH = 68 kJ
OR This reaction also can be carried out in two
distinct steps:
N2(g) + O2(g) = 2NO(g)
ΔH1 = 180 kJ
2NO(g) + O2(g) = 2NO2(g)
ΔH2 = -112 kJ
____________________________________________
_
Net reaction: N2(g) + 2O2(g) = 2NO2(g)

ΔH = ΔH1 + ΔH2 = 68 kJ
Hints for Using Hess’s Law
Calculations involving Hess’s law typically require that
several reactions be manipulated and combined to finally
give the reaction of interest. In doing this procedure you
Should:
• Work backward from the required reaction, using the
reactants and products to decide how to manipulate the
other given reactions at you disposal
• Reverse any reactions as needed to give the required
reactants and products
• Multiply reactions to give the correct numbers of
reactants and products
Hess Rules and More

If the reaction is multiplied (or divided) by
some factor, H must also be multiplied (or
divided) by that same factor.


If the reaction is reversed (flipped), the sign
of H must also be reversed.
Sample Exercise 6.7

Two forms of carbon are graphite, the soft, black,
slippery material used in “lead” pencils and as a
lubricant for locks, and diamond, the brilliant,
hard gemstone. Using the enthalpies of
combustion for graphite (-394 kJ/mol) and
diamond (-396 kJ/mol), calculate Δ H for the
conversion of graphite to diamond:
C graphite(s)  Cdiamond
See page 244 for solution
Sample Exercise 6.8
Calculate the enthalpy of formation of diborane from its
elements according to the equation:
2B(s) + 3H2(g)
B2H6(g)
from the following data:
a.2B(s) + 3/2O2(g)
B2O3(s) DH = -1273 kJ
b.B2H6(g) + 3O2(g)
B2O3(s) + 3H2O(g) DH = -2035 kJ
c.H2(g) + 1/2O2(g)
H2O(l) DH = -286 kJ
d.H2O(g)
H2O(l) DH = -44 kJ
Solution:
This kind of problem is best approached by working backwards
from the required products given the information with which you
are provided. There is no set "formula". Remember to be very
careful to keep your equations balanced and make sure they sum
to the required final equation.
Focus on the boron and diborane: equations (a) and -(b) do what
we want but involve a whole collection of junk not in the final
equation:
FIRST:
(a) 2B(s) + 3/2O2(g)
B2O3(s) DH = -1273 kJ
-(b) B2O3(s) +3H2O(g)
B2H6(g) + 3O2(g) DH = 2035 kJ
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Sum: B2O3(s) + 2B(s) + 3/2O2(s) + 3H2O(g) B2O3(s) + B2H6(g) + 3O2(g) DH = 762 kJ
Or:
2B(s) + 3H2O(g)
B2H6(g) + 3/2O2(g) DH = 762 kJ
Next :
we have to get rid of the H2O(g) and O2(g) and introduce H2.
2B(s) + 3H2O(g)
B2H6(g) + 3/2O2(g) DH = 762 kJ
3x(c) 3H2(g) + 3/2O2(g)
3H2O(l) DH = 3x(-286) kJ
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Sum: 2B(s) + 3H2(g) + 3/2O2(g) + 3H2O(g)
B2H6(g) + 3/2O2(g) + 3H2O(l) DH = -96
kJ
The 3/2O2(g) cancels but not the water which is gas on one side and liquid on the other:
2B(s) + 3H2(g) + 3H2O(g)
B2H6(g) + 3H2O(l) DH = -96 kJ
3x(-d)
3H2O(l)
3H2O(g) DH = 3x44 kJ
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Sum: 2B(s) + 3H2(g) + 3H2O(g) + 3H2O(l)
B2H6(g) + 3H2O(l) + 3H2O(g) DH =
36 kJ
Or: 2B(s) + 3H2(g)
B2H6(g) DH = 36 kJ
Standard Enthalpies of Formation

Many reactions cannot really be studied by calorimetry.
The conversion of graphite to carbon requires enormous
pressure and high temperature. Other processes would
be dangerous: the decomposition of an explosive like
nitroglycerine or diazomethane. The diborane example
showed how it is possible to calculate enthalpies from
other reactions which can be studied. A standard method
of doing this is by starting with heats of formation.
 The Standard Enthalpy of Formation
Δ Hfo of a compound is
defined as the change in enthalpy that occurs when a mole of the
compound is formed from its elements with all substances in their
standard states.
 The Standard State for a substance is a precisely defined
reference state:
○ The standard state for a gas is 1 atm pressure (101 305 Pa) or 1 bar
(100 000 Pa).
○ For normally condensed states, liquid or solid is the standard state.
○ For solutions the standard concentration is 1 M.
○ For an element, the standard state is the normal form of the element at
1 atm and 25oC.

Look again at the reaction for the formation of
NO2 from its elements:

1/2N2(g) + O2(g) + energy(heat)
D Hfo = 34 kJ/mol

One mole of product is formed and all reactants
are in their standard states. See Table 6.2 for
typical heats of formation
NO2(g)
What about methane
 Here is how the enthalpy change for the combustion
of CH4 can be calculated from the standard enthalpies
of formation ( for this to make sense: see Fig 6.8):
CH4(g) + 2O2(g)
CO2(g) + 2H2O(l)
Now: C(s) + H2(g)
CH4(g) ΔHfo = -75 kJ
 Reaction (a) in the figure is the reverse of this.
Reaction (b) is actually no change so ΔH = 0.
 Reaction (c) is another standard formation reaction:
C(s) + O2(g)
CO2(g) ΔHfo = -394 kJ/mol
 and reaction (d) is double the formation of water from
its elements:
 2H2(g) + O2(g)
2H2O(l)2. ΔHfo = -572 kJ
So ΔHoreaction = ΔHo(a) +Δ Ho(b) + ΔHo(c) +Δ Ho(d) = [-Hfo Δfor CH4] + 0 + [ΔHfo for
CO2] + [2. ΔHfo for H2O] = -891 kJ/mol
In General:

where np and nr are numbers of moles:
ΔHoreaction = ∑npHfo(products) - ∑nr ΔHfo(reactants)
Check out A-20 in
the Appendix for
LOTS of enthapies
of formation