* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download p(A)
DNA profiling wikipedia , lookup
Cell-free fetal DNA wikipedia , lookup
SNP genotyping wikipedia , lookup
Quantitative trait locus wikipedia , lookup
Genealogical DNA test wikipedia , lookup
Population genetics wikipedia , lookup
Microevolution wikipedia , lookup
Genetic drift wikipedia , lookup
Dominance (genetics) wikipedia , lookup
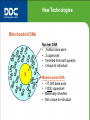
New Technologies Y-STR DNA Pedigree (7 generations) New Technologies Mitochondrial DNA Nuclear DNA • 3 billion base pairs • 2 copies/cell • Inherited from both parents • Unique to individual XX Mitochondrial DNA • ~17,000 base pairs • >1000 copies/cell • Maternally inherited • Not unique to individual New Technologies Mitochondrial DNA - Maternal Lineage Testing • Inherited from the biological mother • Can be used to identify a maternal lineage or genetic reconstructions • Can be used to test hair, bones, teeth because it is less prone to degradation • Can not distinguish between individuals related in the female lineage (brothers, sisters, aunts, uncles) New Technologies Mitochondrial DNA Pedigree (7 generations) New Technologies mtDNA Sequence Comparison Standard: GCATATTGCGCCTAGCATATTGCGCCTACCTA Tested: GCACATTACGTCTAGGATATTGCGCTTACCTA References Basics of Parentage Testing DNA from each person is unique, except for identical twins Each person gets their genomic DNA in equal amounts from their biological parents People who are biologically related share more DNA than those unrelated The genetic odds in favor of paternity are termed “Paternity Index”, PI Paternity Index, PI • Likelihood Ratio • Ratio between X and Y, PI = X / Y • X = chance the alleged father contributed the paternal allele to the child (0, 0.5, or 1) • Y = chance a random, unrelated individual contributed the paternal allele to the child; the frequency of the paternal allele in the ethnic group of interest Example of PI Calculation • • • • • STR analysis at D7S820 Mother = 8,9; Child = 9,10; AF = 10,11 Alleged Father is Caucasian PI = 0.5 / 0.2906 = 1.72 This means that the Alleged Father is 1.72 times more likely to be the biological father than a random, unrelated man of the Caucasian population. Combined Paternity Index • Also referred to as the PI or CPI • The product of the individual paternity indices for all the genetic loci examined. • Each locus must be independent, and unlinked to be multiplied together to produce the combined paternity index. Example of a Combined PI • 13 CODI loci used to examine paternity • Alleged Father not excluded at any locus • PI at each locus as follows: CSF1PO = 3.53, D3S1358 = 2.71; D5S818 = 2.45; D7S820 = 1.72; D8S1179 = 1.95; D13S317 = 3.58; D16S539 = 2.33; D18S51 = 13.61; D21S11 = 2.20; FGA = 4.53; THO1 = 1.01; TPOX = 0.92; vWA = 2.57 Combined Paternity Index • Multiplication of all 13 individual paternity indices • Combined PI = 212,390 • The alleged father is 212,390 times more likely to be the biological father than a random, unrelated man on the same ethnic group Probability of Paternity (W) • Also known as the Likelihood of Paternity, the Plausibility of Paternity, the Relative Chance of Paternity, or the Probability Ratio • Calculated using Bayesian Logic • Incorporates a Prior Probability (Pr) Bayesian Logic • Based on Bayes Theorem (1763) • Foundation for the probabilistic approach used for the evaluation of paternity tests. • Relates the probability of an AF with certain genetic markers being a member of a particular group (Biological Fathers) to the probability that a known member of the group would have the same genetic markers. Bayes Theorem W = Pr . X / (Pr . X + (1 – Pr) . Y) W = Likelihood of an event occurring Pr = Prior Probability X = frequency with which the BF would have the same phenotype as the AF for a specific M – C combination • Y = frequency with which a non-father, ie a randomly selected man, would have the same phenotype as the AF • • • • Essen-Moller Equation • W = 1 / (1+ Y/X) • The mathematical expression of the Relative Chance of Paternity (RCP) of the AF. • Bayes theorem applied to parentage testing. • Hummel modification, W = X/(X + Y), expressed as a percentage • Uses a neutral Prior Probability (Pr) of 0.5 Prior Probability • The probability, after genetic testing, that the AF is the BF. • W is determined by integrating Prior Probability and Paternity Index by means of Bayes theorem. • The Hummel modification of the EssenMoller Equation, where a Prior Probability of 0.5 is assumed, is most often used. • Values range from 0.0 to 1.0 Example of Probability of Paternity Calculation Combined Paternity Index = 50 Assume a Prior Probability of 0.5 W = 50(0.5)/50(0.5) + 1- 0.5 = 25.0 / 25.5 = 98.04% When Prior Probability is 0.5 the Probability of Paternity is PI / 1 + PI Examples of Other Prior Probability Values • If combined PI is 50 and the Prior Probability is 0.9 then • W = 50 (.9)/ 50 (.9) + 1 – 0.9 • = 45 / 45.1 = 99.78 % • If the combined PI is 50 and the Prior Probability is 0.1 then • W = 50 (0.1) / 50 (0.1) + 1- 0.1 • = 5 / 5.9 = 84.75% Effect of the Prior Probability • As the Combined PI gets bigger, the value of the Prior Probability has little effect on the Probability of Paternity • If Combined PI = 10,000 • W when Pr is 0.1 = 99.991% • W when Pr is 0.9 = 99.999% Exclusion of Parentage • The AF is excluded as the biological father when he does not have the obligate paternal alleles • With DNA testing, exclusions in two (2) systems are required before an exclusion is declared. • With STR analysis, most laboratories require exclusions at three (3) loci. Example of an Exclusion • • • • • • • Locus M C AF D7S820 8,9 9,10 11,12 D18S51 12,14 12,17 12,18 THO1 8,9.3 9.3 6,9.3 D8S1179 9,13 12,13 13,14 Combined Paternity Index = 0.00 Probability of Paternity = 0.00% PI 0.00 0.00 1.64 0.00 Mutations Observed when child contains alleles not present in either biological parent. Often result of recombinational event in meiosis in the production of sperm or eggs. With STR analysis, often leads to the presence of an allele one (1) repeat unit larger of smaller than the parent. Example of a Mutation • • • • • • • • • Locus M C AF D7S820 8,9 9,10 11,12 D18S51 12,14 12,17 17,18 THO1 8,9.3 9.3 6,9.3 D8S1179 9,13 12,13 10,12 D21S11 28,30 28,31 31 Combined Paternity Index = 1.08 Probability of Paternity = 51.92% Additional testing required. PI 0.0025 5.45 1.64 3.44 14.01 Paternity Index for Mutation The paternity index at a locus which shows an exclusion which may be due to a mutation is calculated as follows. PI = mutation rate at locus/power of exclusion Example: At D7S820 the mutation rate is 0.0015 The power of exclusion is 0.6 PI = 0.0015 / 0.6 = 0.0025 Power of Exclusion (A) • The ability of a genetic test to exclude a falsely accused man of paternity. • It is dependent upon the actual phenotypes of M and C, and the ethnic group of the M and AF. • RMNE (Random Man Not Excluded) is the frequency with which men selected at random are not excluded as the BF • RMNE = 1 - A When Additional Testing Needed • When only one or two direct exclusions are observed with more than 10 loci tested. • When exclusion is based on indirect exclusions • When the combined PI is less than 100 • When close biological relatives are AFs Direct Exclusion • When both the child and AF are heterozygous and the AF does not have the obligate paternal allele. • Example • Locus M C AF PI • D7S820 8,9 9,10 11,12 0.00 Indirect Exclusion • When both the child and AF are homozygous and the AF does not share the obligate paternal allele. • Example • Locus M C AF PI • D7S820 8,9 9 11 0.00 • Here it is possible that an allele is not detected in C and AF. Mutation Rates • Rates vary at different loci. • Rates vary for maternal and paternal. • Maternal rates determined from calculation of number of times the child does not share an allele with the mother at a locus. • Paternal rates determined from calculation of the number of times child does not share an allele with the BF at a locus. • Large numbers generated from parentage testing laboratories compiled by the AABB. Mutation Rates at CODIS Loci • • • • • • • • Locus D3S1358 D5S818 D7S820 D8S1179 D13S317 D16S539 D18S51 Maternal < 0.0002 0.0004 0.0003 0.0008 0.0006 0.0030 0.0010 Paternal 0.0011 0.0015 0.0015 0.0027 0.0015 0.0090 0.0026 Mutation Rates at CODIS Loci • • • • • • • Locus D21S11 FGA CSF1PO THO1 TPOX vWA Maternal 0.0018 0.0001 0.0003 0.0001 0.0001 0.0004 Paternal 0.0024 0.0029 0.0013 0.0002 0.0002 0.0034 Number of STR Repeat Unit Changes in Mutations # Repeats 1 repeat 2 repeats 3 repeats 4 repeats Other Male 91.9 4.9 1.2 1.6 0.4 Female 91.9 5.8 0.7 0.7 0.9 Total 91.9 5.1 1.1 1.4 0.5 Accreditation of Parentage Testing Laboratories • Accreditation offered by • American Association of Blood Banks (AABB) • American Society for Histocompatibility and Immunogenetics (ASHI) • College of American Pathologists (CAP) PT Laboratories - 2000 44 laboratories accredited by the AABB About 300,00 cases tested (typical case is trio of M, C, and AF) One big lab accounts for about 1/3 of testing 70% of testing done using PCR DNA analysis 30% of testing done using RFLP DNA analysis Proficiency offered through CAP with PI survey AABB Accreditation • Accreditation documents sent to AABB • AABB Standards for Parentage Testing Laboratories, 4th Edition • Standards are in Quality Systems Essentials Format, which is ISO compatible • Assessment performed using Assessment Tool • Accreditation given to laboratories which follow AABB Standards Paternity Index Calculation • • • • Mother Child AF PI = X /Y BD AB AC Paternity Index • X is the probability that 1) M is BD; 2) AF is AC; and 3) C is AB • X is the frequency of this set of three phenotypes among true trios Paternity Index • Y is the probability that 1) M is BD; 2) AF is AC; and 3) C, fathered by the alternative father, is AB • Y is the frequency of this set of three phenotypes among false trios Paternity Index • p(BD) = probability of the BD phenotype • p(AC) = probability of the AC phenotype • Calculated using the Hardy-Weinberg Equation (2pq) • The conditional probability of the C phenotype, given the phenotypes of its parents, is computed from Mendel’s First Law, the Principle of Segregation. Paternity Index • The formula for the numerator X is: • X = p(BD) . p(AC) . [(0 . 0) + (0.5 . 0.5)] • = p(BD) . P(AC) . 0.25 • The third term is the probability that a C of a BD M and and AC father will be phenotype AB. When the C is heterozygous there are two components, in that an AB C can inherit A from the M and B from the father and vice versa. Paternity Index • The formula for the denominator Y is: • Y = p(BD) . p(AC) . [(0 . b) + (0.5 . a)] • = p(BD) . p(AC) . 0.5 . a • The third term is the probability the C of a BD mother will be AB. • It is the probability she will contribute an A allele (0) and the alternative father will contribute a B allele (b), plus vice versa. Paternity Index • When mating is random, the probability that the alternative father will contribute a specific allele to the C is equal to the allele frequency in his ethnic group. • This is true whether or not the population is in H-W equilibrium at the locus. Paternity Index • PI = [p(BD) . p(AC) . 0.25] / [p(BD) . p(AC) . (0.5 . a)] • = 1 / 2a • The formula does not contain phenotype frequencies, thus is does not assume H-W equilibrium. • This is true for any system in which the genotypes can be determined unambiguously from the phenotype, like DNA. Paternity Index • M C AF X Y PI RMNE • BD AB AC 0.25 0.5a 1/2a a(2-a) • BC AB AC 0.25 0.5a 1/2a a(2-a) • BC AB AB 0.25 0.5a 1/2a a(2-a) • BC AB A 0.50 0.5a 1/a a(2-a) • B AB AC 0.50 a 1/2a a(2-a) • B AB AB 0.50 a 1/2a a(2-a) • B AB 1.00 a 1/a a(2-a) A Paternity Index • M C AF X Y PI RMNE • AB AB AC 0.25 0.5(a+b) 1/[2(a+b)] (a+b)(2-a-b) • AB AB AB 0.50 0.5(a+b) 1/(a+b) (a+b)(2-a-b) • AB AB 0.50 0.5(a+b) 1/(a+b) (a+b)(2-a-b) • AB A AC 0.25 0.5a 1/2a a(2-a) • AB A AB 0.25 0.5a 1/2a a(2-a) • AB A A 0.50 0.5a 1/a a(2-a) • A A AB 0.50 a 1/2a a(2-a) • A A A 1.00 a 1/a a(2-a) A Motherless Paternity Index Calculations • The assumption in calculating X is that the AF is the BF • The assumption in calculating Y is that the AF and C are unrelated • Let the phenotypes of the AF = AC and the C = AB Motherless Paternity Index Calculations • X is the probability that 1) the AF is phenotype AC; and 2) the C is phenotype AB • X = p(AC) . (0.5 . b + 0 . a) = p(AC) . 0.5 . b • p(AC) is the probability of the AF phenotype; 0.5 is the probability that an AC man will contribute an A allele; b is the probability that an untested woman will contribute a B allele; 0 is the probability than an AC man will contribute a B allele; a is the probability the woman will contribute an A allele. Motherless Paternity Index Calculations • Y is the probability that 1) a man chosen at random is phenotype AC; and 2) the child, the offspring of two untested parents, neither of whom are related to the AF, is phenotype AB (the probability of getting an A allele from one parent and a B allele from the other, assuming independence). • Y = p(AC) . 2ab Motherless Paternity Index Calculaation • PI = [p(AC) . 0.5 . b] / [p(AC) . 2ab] • = 1 / 4a • This formula does not assume H-W equilibrium because it involves only allele frequencies, not genotype or phenotype frequencies. Motherless Paternity Index • C AF X Y PI • AB AC 0.5b 2ab 1/4a • AB AB • AB RMNE (a+b)(2-a-b) 0.5(a+b) 2ab (a+b)/4ab (a+b)(2-a-b) A b 2ab 1/2a (a+b)(2-a-b) • A AC 0.5a a2 1/2a a(2-a) • A A a a2 1/a a(2-a) Power of Exclusion • 1 – RMNE • Combined Probability of Exclusion (CPE) refers to the Average Power of Exclusion • PEAVG = h2 . [1 – 2hH2] • H = frequency of Homozygosity • h = frequency of Heterozygosity Reconstructions • If the parents of the AF are available for testing, a grandparental paternity index can be calculated. • If the AF has no known offspring, his genotype generally can not be determined. • When both parents of the AF are available, the AF’s genotype can be reduced to 4 or less. Reconstruction The No-Father Case • M = BC and C = AB • Paternal allele = A • AF deceased, but some of his relatives are available for testing • The goal is to determine as precisely as possible the AF genotype then calculate the probability of transmitting the A allele • p(A) = probability of transmitting A allele Paternity Index No-Father Case • p(A) = probability AF will transmit A allele to his offspring • X = 0.5 p(A) • Y = 0.5 a • PI = 0.5 p(A) / 0.5 a = p(A) / a Reconstruction • AF M C1 C2 • BC AB AC • What is the PI of the deceased AF based on this data? • Since both children have inherited an A allele from the AF, this increases the probability the AF is AA Reconstruction • • • • • Allele frequencies used for calculations: A = 0.042 B = 0.089 C = 0.037 D = 0.122 Reconstruction 1 2 3 4 5 6 AF Wife Genotype Frequencies p (AB) & p (AC) p (Parents & AF Wife Children Children) AA BC 0.0018 0.0066 1/4 2.9044E-06 AX BC 0.0805 0.0066 1 / 16 3.3124E-05 AA genotype = 0.04202 = 0.0018 AX genotype = 2 . 0.0420 . 0.9580 = 0.805 Reconstruction 1 2 3 4 5 6 AF Wife Genotype Frequencies p (AB) & p (AC) p (Parents & AF Wife Children Children) AA BC 0.0018 AX BC 0.0805 0.0066 0.0066 1/4 1 / 16 BC genotype = 2 . 0.0890 . 0.0370 = 0.0066 Column 5 calculated by Mendelian Law Column 6 product of columns 3 x 4 x 5 2.9044E-06 3.3124E-05 Reconstruction • • • 1 6 P(Parents & AF Children) • • AA AX • Column 7 = relative probability of AF genotype in column 1; divide the number in column 6 by the sum of column 6 (ie 2.9044E06 / 3.60284E-05 = 8.06 %) • Column 8 = conditional probability AF will transmit A allele given the genotype in column 1 2.9044E-06 3.3124E-05 7 Relative Probability 8 Conditional p (A) 9 p (A) 8.06% 91.94% 1.00 0.50 0.0806 0.4597 Reconstruction • • • 1 6 P(Parents & AF Children) • • AA AX • Column 9 = probability that the AF will transmit the A allele given the genotype in column 1; multiply column 7 x 8 • p(A) = 0.5403 = (0.0806 + 0.4597) • PI = p(A) / a = 0.5403 / 0.0420 = 12.86 2.9044E-06 3.3124E-05 7 Relative Probability 8 Conditional p (A) 9 p (A) 8.06% 91.94% 1.00 0.50 0.0806 0.4597 Avuncular Index (AI) • AI is the likelihood ratio for the hypothesis that the tested man’s brother is the true BF, as opposed to a random man. • Typical scenario is an AF is excluded and the residual PI is >1,000 (multiplication of all PI s from non-excluding loci). • The tested AF is not the BF, but it is likely that the BF may be a relative of the AF Avuncular Index • PI = X /Y • On average, the AF and his brother share 50% of their alleles, the remaining 50% of the untested brother’s alleles are selected at random from the population. • Thus the X value for the untested brother is the average of the X value for the tested AF and the X value for an untested man. Avuncular Index • Thus X = X + Y / 2 = 0.5X + 0.5 Y • The denominator is Y. • AI = 0.5X + 0.5Y / Y • = PI +1 / 2 Calculation of Likelihood Ratio for any Relative of Tested Man • = R * X + (1- R) * Y / Y = R * PI + 1 – R • R = Coefficient of Relationship; it tells the proportion of the relative’s alleles expected to be identical by decent with those of the tested man. The remainder (1 – R) are random. Coefficient of Kinship (F) • From each of two individuals, randomly select an allele from a given locus. • F is the probability that the two alleles are identical by descent. Coefficient of Relationship (R) • For two individuals, R is the proportion of alleles at a given locus that are identical by descent. • For two individuals who are not inbred, R = 2F Coefficients of Kinship and Relationship • • • • • • • • • • Relationship Parent & Child Siblings Half Siblings Grandparent & GC Uncle & Niece/Neph First Cousins Second Cousins Third Cousins Identical Twins F 0.25 0.25 0.125 0.125 0.125 0.0625 0.015625 0.003906 0.5 R 0.50 0.50 0.25 0.25 0.25 0.125 0.032125 0.00781 1.00 Kinship Analysis • Determine whether two individuals are blood relatives when no other family members are available for testing. • Requires a randomly mating population, and testing of several independent, highly polymorphic loci. • Absence of silent alleles (null alleles) allows phenotypes to denote genotypes. Kinship Analysis • If two parents are genotype AB and CD, they can have offspring with the four equally frequency genotypes: • • Parent 1 Parent 2 Possible Genotype Genotype Offspring • • Frequency Genotype AB CD AC 0.25 AD BC BD At each locus, 2, 1, or 0 alleles shared 0.25 0.25 0.25 Kinship Analysis • Consider two non-inbred individuals, s1 and s2. • To evaluate the hypothesis that S1 and S2 are related, calculate the likelihood ratio: • LR = X/Y • X = probability of s2 if s1 and s2 related • Y = probability of s2 if s1 and s2 unrelated Kinship Analysis • Calculation of Y is simply the genotype frequency of s2 calculated from the HardyWeinberg equation: p2 + 2pq +q2 = 1 Kinship Analysis • Calculation of X • If s1 and s2 are related, then the observed genotype of s2 could arise in one of three ways. • 1. Two alleles of s1 and s2 are identical (k2) • 2. One allele of s1 and s2 are identical (2k1) • 3. No alleles of s1 and s2 are identical (k0) Kinship Analysis • The k coefficients for two related people, S and T is as follows: • Let A and B be the parents of S. • Let C and D be the parents of T. • k2 is determined by the coefficients of kinship (F) between parents S and T. Kinship Analysis • • • • • Calculation of the k Coefficients k2 = (FAC* FBD) + (FAD* FBC) 2k1 = 4FST - 2k2 k1 = 2FST - k2 k0 = 1 – k2 – 2k1 Kinship Analysis • F and k Coefficients • Relationship F k2 • Parent-Child • Full Siblings ¼ ¼ • Half Sibling 1/8 0 • GP-GC 1/8 0 • Uncle-Niece 1/8 0 • • First Cousins Second Cousins 1/16 0 0 1/64 2k1 k1 k0 0 1 ½ 0 ¼ ½ ½ ½ ½ ¼ ¼ ¼ ¼ ¼ 1/8 ¼ ½ ½ ½ ¾ 1/16 1/32 15/16 Kinship Anlysis s1 s2 X Y X/Y AA AA 1* k2 + a * k1 + a * k1 + a2 * k0 a2 (k2 + 2k1a + k0a2) / a2 AA AB 0 * k2 + b * k1 + b * k1 + 2ab * k0 2ab AA BB 0 * k 2 + 0 * k1 + b2 + k 0 b2 k0 AA BC 0 * k2 + 0 * k1 + 2bc + k0 2bc k0 AB AB 1* k2 + b * k1 + a * k1 + 2ab * k0 2ab (k2 + k1a + k1b+k02ab) / a2 AB AA 0 * k2 + a * k1 + a2 * k0 a2 (k1 + k0a) / a AB AC 0 * k2 + c * k1 +2ac * k0 2ac (k1 +2 k0a) /2 a AB CD 0 * k2 + 0 * k1 +2cd * k0 2cd k0 (k1 + k0a) / a Kinship Analysis Example • What is the likelihood the two individuals are full siblings? Locus 1 • • • • • Locus 2 Al Sib 1 A,B C,D Al Sib 2 A,B C,E Frequency of A allele = 0.05 Frequency of B allele = 0.05 Frequency of C allele = 0.05 Locus 3 F,G H,I Kinship Analysis Example • Locus 1: • X/Y = (k2 + k1a + k1b + k02ab) / 2ab • = (0.25) + (0.25)(0.05) + (0.25)(0.05) + (0.25)(0.005) / 0.005 • = 0.27625 / 0.005 • = 55.25 Kinship Analysis Example • • • • • Locus 2: X / Y = k1 + 2k0a / 2a = 0.25 + (2)(0.25)(0.05) / 0.10 = 0.275 / 0.10 = 2.75 Kinship Analysis Example • Locus 3 • X / Y = k0 • = 0.25 Kinship Analysis Example • The combined Sib Index, SI, (likelihood of the two alleged sibs being full siblings) is the multiplication of each of the individual indices. • SI = 55.25 * 2.75 * 0.25 = 37.98 • This is a strong indication that the two are related as full siblings. Kinship Analysis Example • What is the likelihood that the two individuals are related as half siblings? • Use the same formulas, but use the halfsibling values for the k coefficients. Kinship Analysis Example • Locus 1: • X/Y = (k2 + k1a + k1b + k02ab) / 2ab • = (0) + (0.25)(0.05) + (0.25)(0.05) + (0.50)(0.005) / 0.005 • = 0.0275 / 0.005 • = 5.5 Kinship Analysis Example • • • • • Locus 2: X / Y = k1 + 2k0a / 2a = 0.25 + (2)(0.50)(0.05) / 0.10 = 0.3 / 0.10 = 3.0 Kinship Analysis Example • Locus 3 • X / Y = k0 • = 0.50 Kinship Analysis Example • The combined Sib Index, SI, (likelihood of the two alleged sibs being half siblings) is the multiplication of each of the individual indices. • SI = 5.5 * 3.0 * 0.5 = 8.25 • This is weak evidence that the two are related as half siblings. • The two are 4.6 times more likely to be full siblings (37.98 / 8.25) than half siblings.