Download NorwayWN.5

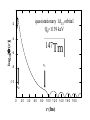
Threshold anomaly
E.P. Wigner, Phys. Rev. 73, 1002 (1948), the Wigner cusp
G. Breit, Phys. Rev. 107, 923 (1957)
A.I. Baz’, JETP 33, 923 (1957)
A.I. Baz', Ya.B. Zel'dovich, and A.M. Perelomov, Scattering Reactions and Decay
in Nonrelativistic Quantum Mechanics, Nauka 1966
A.M. Lane, Phys. Lett. 32B, 159 (1970)
S.N. Abramovich, B.Ya. Guzhovskii, and L.M. Lazarev, Part. and Nucl. 23, 305 (1992).
• The threshold is a branching point.
• The threshold effects originate in conservation of the flux.
• If a new channel opens, a redistribution of the flux in other open
channels appears, i.e. a modification of their reaction cross-sections.
• The shape of the cusp depends strongly on the orbital angular
momentum.
Y(b,a)X
X(a,b)Y
a+X
a+X
a1+X1 at Q1
a2+X2 at Q2
an+Xn at Qn
Threshold anomaly (cont.)
Studied experimentally and theoretically in various areas of physics:
pion-nucleus scattering
R.K. Adair, Phys. Rev. 111, 632 (1958)
A. Starostin et al., Phys. Rev. C 72, 015205 (2005)
electron-molecule scattering
W. Domcke, J. Phys. B 14, 4889 (1981)
electron-atom scattering
K.F. Scheibner et al., Phys. Rev. A 35, 4869 (1987)
ultracold atom-diatom scattering
R.C. Forrey et al., Phys. Rev. A 58, R2645 (1998)
Low-energy nuclear physics
•charge-exchange reactions
•neutron elastic scattering
•deuteron stripping
The presence of cusp anomaly could provide structural information about
reaction products. This is of particular interest for neutron-rich nuclei
C.F. Moore et al., Phys. Rev. Lett. 17, 926 (1966)
N. Michel et al. PRC 75, 0311301(R) (2007)
WS potential depth decreased to
bind 7He. Monopole SGI strength
varied
5He+n
6He
Overlap integral, basis
independent!
6He+n
7He
Anomalies appear at calculated
thresholds (many-body Smatrix unitary)
Scattering continuum essential
see also Nucl. Phys. A 794, 29 (2007)
• The non-resonant continuum is important for the spectroscopy of weakly bound nuclei
(energy shifts of excited states, additional binding,…)
• SFs, cross sections, etc., exhibit a non-perturbative and non-analytic behavior (cusp
effects) close to the particle-emission thresholds. These anomalies strongly depend on
orbital angular momentum
• Microscopic CSM (GSM) fully accounts for channel coupling
Timofeyuk, Blokhintsev, Tostevin, Phys. Rev. C68, 021601 (2003)
Non-Borromean two-neutron halos
Helium resonances in the Coupled Cluster approach and Berggren basis
Complex coupled-cluster approach to an ab-initio description of open quantum systems, G.
Hagen, D. J. Dean, M. Hjorth-Jensen and T. Papenbrock, Phys. Lett. B656, 169 (2007)
Real Energy Treatment
Hilbert space formulation : Shell Model Embedded in the Continuum (1999)
Open space involves
particles in the scattering
continuum
Closed space: SM space
Q0  A
Q1  A 1  1
A
Q2  A  2  2
Q  1
i
i 0
HQ1Q2
...  ...
HQ0Q0
HQ1Q1



HQ0Q0  HQeff0Q0 E 




H
eff
Q0Q0

E  
SM
j
 
SM
i
H Q 0Q 0 
HQ0Q0

HQ0Q2
HQ1Q1
HQ2Q2

   c  c  i 
i j
'
c c

  P
dE


j


i
' 

E  E  2 c1
c1  c

SM
j
real



SM
i
HQ0Q1
HQ2Q2
imaginary
coupling between closed and open space. It
vanishes if E<Ec
From M. Ploszajczak
Continuum Shell Model
He isotopes
•Cross section and structure
within the same formalism
•Reaction l=1 polarized elastic
channel
References
[1] A. Volya and V. Zelevinsky,
Phys. Rev. Lett 94 (2005) 052501.
[2] A. Volya and V. Zelevinsky,
Phys. Rev. C 67 (2003) 54322
Hagen et al, ORNL/UTK
Ab initio: Reactions
Nollett et al, ANL
Coupled
Clusters
CC
GFMC
Quaglioni & Navratil, LLNL 2008
No Core Shell Model
+ Resonating Group
Method
11Be:
Phys. Rev. C 79, 044606 (2009)
Description of Proton Emitters
ln 2 / T1/ 2  Ze / Rc  Qp,nucl 
1/ 2
2
Gjl  2m /
Unbound
states
Discrete
(bound)
states
F
2

Rout
Ri n
exp2Gjl 
dr V jl r  VCoulr  Vl r  Qp, nucl
0
daughter
proton
p
  2T
2
i f
quasistationary 1d3/2 orbital
Qp=1139 keV
log10|(r)|
-2
-4
147Tm
-6
r2
-8
-1 0
rB
0
20
40
60
80
10 0 12 0 14 0 16 0 18 0
r (fm)
147Tm
log10 t1/2 (sec)
10
146Er+p
exp
0h11/2
1d3/2
2s1/2
5
0
-5
-1 0
Qp window
0.5
1.0
1.5
Qp (MeV)
2.0
2.5
Fine structure in proton emission studied at HRIBF
7 ms
1/2+
3 ms
4 ms
7/2-
145Tm
141Ho
~2%
2+
202
ORNL 2001
ORNL 2005
~1% 480
146Tm
20,15%
ORNL 2003
T.N. Ginter et al.,
PRC 68, 034330, 2003
M.N. Tantawy et al.,
PRC 73, 024316, 2006
2+
0 keV
0+
M. Karny et al.,
PRL 90, 012502, 2003
K. Rykaczewski et al.,
AIP 638, 149, 2002
M. Karny et al.,
PRL 2006
(5-)
330
144Er
0 keV 0+
140Dy
70 ms
10%
ORNL 2000
0.9%
198 ms (10+)
11/2-
1.9 ms (10+)
nh11/2 x 2+
250
nh11/2
180
ns1/2 x
0 keV ns1/2
145Er
2+
144Tm
ORNL 2004
~30%
270+x nh11/2 x 2+
nh11/2
x
0 keV
ns1/2
143Er
R. Grzywacz et al.,
EPJ A25, s01, 145, 2005
Some References
Particle-core vibration coupling
C.N.Davids, H.Esbensen, Phys.Rev. C69, 034314 (2004)
M.Karny et al., Phys.Rev.Lett. 90, 012502 (2003)
K.Hagino, Phys.Rev. C64, 041304 (2001)
C.N.Davids, H.Esbensen, Phys.Rev. C64, 034317 (2001)
H. Esbensen and C.N. Davids, Phys. Rev. C64, 034317 (2001)
Deformed proton emitters, coupled-channels, R-matrix
B.Barmore et al., Phys.Rev. C62, 054315 (2000)
H.Esbensen, C.N.Davids, Phys.Rev. C63, 014315 (2001)
W.Krolas et al., Phys.Rev. C65, 031303 (2002)
A.T. Kruppa and W. Nazarewicz, Phys.Rev. C69, 054311 (2004)
M. Karny et al., Physics Letters B664, 52 (2008)
BCS treatment of pairing
G.Fiorin, E.Maglione, L.S.Ferreira, Phys.Rev. C67, 054302 (2003)
A.T. Kruppa and W. Nazarewicz, Phys. Rev. C69, 054311 (2004)
Test case:deformed WS+Coulomb potential for
b2=0.244, kmax=2 fm-1, lmax=11, Nscat=60
141Ho
Ground-state 2p radioactivity
50_463
1

0
1
-1

1
0
0
Light intensity [a.u.]
6
-1
PMT
-1
4
1 = (104  2)°, 1 = (70  3)°
2
 = (142  3)º  pp = (143  5)º
0
0.534
0.536
Time after implantation [ms]
0.538
Energy - angle 2D correlation
45Fe
16
18
14
16
12
10
14
8.0
12
6.0
10
4.0
8
2.0
0
6
4
2
0.8
-1.0
0.6
-0.5
Q
E/
0.4
0.0
0.5
2p
0.2
c
)

pp
(
os
1.0
3-body model prediction
25% p2 + 75% f2
Experiment
Summary
Coupling of nuclear structure and reaction theory
• Nuclei are open quantum many body systems.
• Tying nuclear structure directly to nuclear decays and
reactions within a coherent framework is an important goal.
• Ab-initio methods, continuum shell model, and modern
mean field theories allow for the consistent treatment of
open channels, thus linking the description of bound and
unbound nuclear states and direct reactions.
• The battleground in this task is the territory of weakly bound
nuclei where the structure and reaction aspects are
interwoven.
Thank You
Backup
Complex Scaling
Introduced in the early 1970s in atomic physics to guarantee that wave functions
and resonances are square integrable.
Uniform complex
scaling
The transformed Hamiltonian is no longer hermitian as it acquires a complex
potential. However, for a wide class of local and nonlocal potentials, called dilationanalytic potentials, the so-called ABC is valid:
•The bound states of h and h are the same;
•The positive-energy spectrum of the original Hamiltonian h is rotated down by an
angle of 2 into the complex-energy plane;
•The resonant states of h with eigenvalues En satisfying the condition |arg(En)|<2
are also eigenvalues h and their wave functions are square integrable.
Myo, Kato, Ikeda, PRC C76, 054309 (2007)
Theoretical Description of the Fission Process
240Pu
N,Z
elongation
necking
split
N1,Z1
N=N1+N2
Z=Z1+Z2
N2,Z2
Adiabatic Approaches to Fission
WKB:
collective inertia
(mass parameter)
multidimensional space of
collective parameters
V(q)
The action has to be minimized by,
e.g., the dynamic programming
method. It consists of calculating
actions along short segments
between adjacent, regularly spaced
hyperplanes, perpendicular to the qdirection [A. Baran et al., Nucl. Phys.
A361, 83 (1981)]
E
q
Multimodal fission in nuclear DFT
A. Staszczak, A.Baran,
J. Dobaczewski, W.N.
Kinetic Energy and Mass Distributions
in HFB+TDGCM(GOA)
238U
one-dimensional
dynamical
Wahl (experiment)
• Time-dependent microscopic
collective Schroedinger equation
• Two collective degrees of freedom
• TKE and mass distributions
reproduced
• Dynamical effects are responsible
for the large widths of the mass
distributions
• No free parameters
HFB + Gogny D1S + Time-Dependent GOA
H. Goutte, P. Casoli, J.-F. Berger, D. Gogny, Phys. Rev. C71, 024316 (2005)