Download A Solution to the Li Problem by the Long Lived Stau

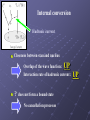
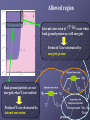
7
A Solution to the Li Problem
by the Long Lived Stau
Masato Yamanaka
Collaborators
Toshifumi Jittoh, Kazunori Kohri,
Masafumi Koike, Joe Sato, Takashi Shimomura
Phys. Rev. D78 : 055007, 2008 and arXiv : 0904.××××
Contents
1, Introduction
2, The small dm scenario and long lived stau
3, Solving the 7Li problem by the long lived stau
4, Relic density of stau at the BBN era
5, Summary
Introduction
Big Bang Nucleosynthesis
(BBN)
Yellow box
Observed light element abundances
[CMB] vertical band
Cosmic baryon density obtained
from WMAP data
Color lines
Light element abundances as
predicted by the standard BBN
Prediction of the light elements abundance
consistent !
Primordial abundance obtained
from observations
[ B.D.Fields and S.Sarkar (2006) ]
7
Li problem
Theory
－10
( 4.15＋0.49
)×10
－0.45
A. Coc, et al.,
astrophys. J. 600, 544(2004)
Observation
－10
( 1.26＋0.29
)×10
－0.24
P. Bonifacio, et al., astro-ph/0610245
7 abundance
Predicted 7Li abundance ≠ observed Li
7
Li problem
Requirement for solving the 7Li problem
Able to destroy a nucleus
Requirement for
solving the Li problem
To occur at the BBN era
Not a Standard Model (SM) process
Possible to be realized in a framework of
minimal supersymmetric standard model !
Coupling with a hadronic current
Stau
t
~
Superpartner of tau lepton
Able to survive still the BBN era
Exotic processes are introduced
The small dm scenario
and long lived stau
Setup
Minimal Supersymmetric Standard Model
(MSSM) with R-parity
Lightest Supersymmetric Particle (LSP)
～
Lightest neutralino c
～
c
～
～
～0
～0
= N1 B + N2 W + N3 Hu + N4 Hd
Next Lightest Supersymmetric Particle (NLSP)
t
Lighter stau ～
t = cos q t ～
tL + sinq t e-igt ～
tR
～
Dark matter and its relic abundance
Dark Matter (DM)
Neutral, stable (meta-stable),
weak interaction, massive
Good candidate : LSP neutralino
DM relic abundance
W DM h 2 = 0.1099 ± 0.0062
∝
m DM × n DM
m DM = (constant) n1
DM
http://map.gsfc.nasa.gov
Naïve calculation of neutralino relic density
DM reduction process
Neutralino pair annihilation
～
c
SM particle
～
c
SM particle
Not enough to reduce the DM number density
m DM = (constant) n1
DM
Not consistent !
m～c > 46 GeV
[ PDG 2006 (J. Phys. G 33, 1 (2006)) ]
Coannihilation mechanism
[ K. Griest and D. Seckel PRD43(1991) ]
DM reduction process
Neutralino pair annihilation
～
c
～
c
+
～
c
SM particle
+
SM particle
stau-neutralino coannihilation
～
t
SM particle
SM particle
Possible to reduce DM number density efficiently !
Requirement for the coannihilation to work
mNLSP – mLSP
<
~ 10 %
mLSP
Long lived stau
Attractive parameter region in coannihilation case
dm ≡ NLSP mass ｰ LSP mass < tau mass
(1.77GeV)
NLSP stau can not two body decay
Stau has a long
lifetime due to phase
space suppression !!
Stau lifetime
BBN era
t
～ survive until BBN era
Stau provides additional processes
to reduce the primordial 7Li abundance !!
Solving the Li problem
by the long lived stau
7
Destruction of nuclei with free stau
～
c
nt A(Z±1)
Negligible due to
Cancellation of destruction
Smallness of interaction rate
t
～±
A(Z)
Interaction time scale (sec)
Stau-nucleus bound state
Key ingredient for solving the 7Li problem
Negative-charged stau can form a bound state with nuclei
~ nuclear radius
･･stau
・・nucleus
Formation rate
Solving the Boltzmann Eq.
New processes
Stau catalyzed fusion
Internal conversion in the bound state
Stau catalyzed fusion
[ M. Pospelov, PRL. 98 (2007) ]
･･stau
Weakened coulomb
barrier
・・nucleus
Nuclear fusion
( ): bound state
Ineffective for reducing 7Li and 7Be
∵ stau can not weaken the barrieres of Li3+ and Be4+ sufficiently
Constraint from stau catalyzed fusion
Standard BBN process
Catalyzed BBN process
Catalyzed BBN cause over
production of Li
Constraint on stau life time
Internal conversion
Hadronic current
Closeness between stau and nucleus
Overlap of the wave function :
UP
Interaction rate of hadronic current :
t
~+ does not form a bound state
No cancellation processes
UP
Internal conversion rate
The decay rate of the stau-nucleus bound state
GIC = | y
|2
・ (s v )
| y |2:
The overlap of the wave functions
( s v ) : Cross section × relative velocity
The bound state is in the S-state of a hydrogen-like atom
| y |2 =
1
pa
3
nucl
anucl =
nuclear radius ～
= 1.2 × A1/3
( s v ) is evaluated by using ft-value
( s v ) ∝ ( ft )– 1
ft-value of each processes
7Be
→ 7Li ・･･ ft = 103.3 sec (experimental value)
7Li
→ 7He ･･･ similar to 7Be → 7Li (no experimental value)
Interaction time scale (s)
Interaction rate of Internal conversion
Very short time scale
significant process for reducing 7Li abundance !
New interaction chain reducing 7Li and 7Be
Internal conversion
7 He
7 Be
7 Li
～
t
～
t
～
Internal conversion
c ,n t
～
c ,n t
Scattering with
background particles
4 He, 3 He,
D, etc
proton, etc
Numerical result for solving the 7Li problem
10-11
10-12
m DM = 300 GeV
10-13
Y~
t
Y~t
-14
10
n~t
s
n~t : number density
of stau
-15
10
s
10-16
0.01
0.1
1
Mass difference between stau and neutralino (GeV)
: entropy density
Allowed region
(7 – 10) × 10-13
100 - 120 MeV
The 7Li problem is solved
Strict constraint on d m and Y~
t
dm = (100 – 120) MeV
Y~t = (7 – 10) × 10-13
Allowed region
~
t
Internal conversion of ( 7 Be) occur when
back ground protons are still energetic
Produced 7Li are destructed by
energetic proton
Back ground particles are not
energetic when 7Li are emitted
Produced 7Li are destructed by
internal conversion
Forbidden region
Overclosure of the universe
Stau decay before
forming a bound state
• Lifetime of stau
• Formation time of
Bound states are not
formed sufficiently
Insufficient reduction
Over production of 6Li
due to stau catalyzed fusion
Relic density of
stau at the BBN era
For the prediction of parameter point
Stau relic density at the BBN era
Not a free parameter !
Value which should be calculated from other parameters
For example
DM mass, mass difference between stau and neutralino, and so on
Calculating the stau relic density at the BBN era
We can predict the parameters more precisely,
which provides the solution for the 7Li problem
The evolution of the number density
Boltzmann Eq. for neutralino and stau
i, j : stau and neutralino
X, Y : standard model particle
n (n eq ) : actual (equilibrium) number density
H : Hubble expansion rate
The evolution of the number density
Boltzmann Eq. for neutralino and stau
Annihilation and inverse annihilation processes
ij
XY
Sum of the number density of SUSY particles is
controlled by the interaction rate of these processes
The evolution of the number density
Boltzmann Eq. for neutralino and stau
Exchange processes by scattering off the cosmic thermal background
iX
jY
These processes leave the sum of the number density
of SUSY particles and thermalize them
The evolution of the number density
Boltzmann Eq. for neutralino and stau
Decay and inverse decay processes
i
jY
Can we simplify the Boltzmann Eq. with ordinal method ?
In the calculation of LSP relic density
All of Boltzmann Eq. are summed up
( all of SUSY particles decay into LSP )
∴
Single Boltzmann Eq. for LSP DM
∴
Absence of exchange terms (
cancel out )
In the calculation of relic density of long lived stau
We are interesting to relic density of NLSP
Obviously we can not use the method !
We must solve numerically a coupled set of
differential Eq. for stau and neutralino
Significant process for stau relic density calculation
Boltzmann Eq. for neutralino and stau
Annihilation process
Exchange process
Due to the Boltzmann factor, n i , n j << n X , n Y
Annihilation process rate << exchange process rate
Freeze out temperature of sum of
number density of SUSY particles
≠
Freeze out temperature of number
density ratio of stau and neutralino
Exchange process
DM freeze out temperature
T DM ~
mDM
5 GeV - 50 GeV
20
( DM mass 100 GeV - 1000 GeV )
Exchange process for NLSP stau and LSP neutralino
~ g
t
~
tt
~
c
t
~
c g
After DM freeze out, number density ratio is still varying
Numerical calculation
Boltzmann Eq. for the number density of stau and neutralino
Yi
ni s
ni : number density of particle i
s : entropy density
Numerical result (prototype)
Tau decoupling
temperature (MeV)
Mass difference between
tau and neutralino (MeV)
Ratio of stau relic density
and current DM density
60
60
80
80
50
100
50
100
15 %
3%
8%
1.5 %
Significant temperature for the calculation of stau number density
・ Tau decoupling temperature
・ Freeze out temperature of exchange processes
Tau decoupling temperature
Condition ( tau is in thermal bath )
[ Production rate ] > [ decay rate, Hubble expansion rate ]
Production processes of tau
g g
l l
q q
tt
tt
tt
Tau decoupling temperature
~ 120 MeV
Summary
We investigated solution of the Li problem in the MSSM, in which
the LSP is lightest neutralino and the NLSP is lighter stau
Long lived stau can form a bound state with nucleus and
provides new processes for reducing Li abundance
Stau-catalyzed fusion
Internal conversion process
We obtained strict constraint on the mass difference between
stau and neutralino, and the yield value of stau
Stau relic density at the BBN era strongly depends on the tau decoupling
temperature and mass difference between stau and neutralino
Our goal is to predict the parameter point precisely by calculating
the stau relic density and nucleosynthesis including new processes
Appendix
Effective Lagrangian
mixing angle
between
and
CP violating phase
Weak coupling
Weinberg angle
Bound ratio
Red : consistent region with DM abundance
and mass difference < tau mass
Yellow : consistent region with DM abundance
and mass difference > tau mass
The favored regions of the muon anomalous magnetic moment
at 1s, 2s, 2.5s, 3s confidence level are indicated by solid lines