* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download DFT on Cyclic(alkyl)(amino)carbenes
Bell's theorem wikipedia , lookup
EPR paradox wikipedia , lookup
X-ray fluorescence wikipedia , lookup
Perturbation theory (quantum mechanics) wikipedia , lookup
Hidden variable theory wikipedia , lookup
Matter wave wikipedia , lookup
Wave–particle duality wikipedia , lookup
Molecular Hamiltonian wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Density functional theory wikipedia , lookup
Hydrogen atom wikipedia , lookup
Chemical bond wikipedia , lookup
Hartree–Fock method wikipedia , lookup
Coupled cluster wikipedia , lookup
Atomic theory wikipedia , lookup
Tight binding wikipedia , lookup
Atomic orbital wikipedia , lookup
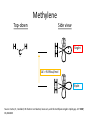
Structure of Presentation • Theory and Computation – Methods: HF, DFT (B3LYP), MP2 – Basis sets: 6-31g*, 6-31g**, cc-pvtz • Molecules of Interest – Methylene (H2C) Theory and Computation Methods and Basis Sets Quantum Mechanics (and Math) (review) • H = E • Time-dependent wave equation: • we are most interested in the energy of stationary states and thus can ignore the phase Kinetic Energy Potential Energy Quantum Mechanics (and Math) (review) • In molecules we must treat each particle this way! (nucleus + electrons) • Molecular Hamiltonian: Ke nuclei Ke e- Ue-n Ue-e Un-n Methods Born-Oppenheimer Approximation: Hartree-Fock Method • Accounts for electron exchange – anti-symmetric exchange or spin wave functions • but not for correlation – Mean field approximation True Correlation Mean-field Methods • HF Etrue= EHF + Ecorr • Moller – Plesset 2nd order (MP2) – Perturbation model – Finds solutions by adding a “correction” to HF • DFT • Uses densities instead of wavefunctions • Different functionals treat Exc differently Source: Sousa, S. et al General Performance of Density Functionals . J. Phys. Chem. A 2007, 111, 1043910452 Functionals I have been using B3LYP *most popular in literature* In B3LYP: EHF parameter is semi-empirically obtained a, b, and c are optimized on a set of known molecules - Thus “Hybrid” a = 0.2 b = 0.72 c = 0.81 Source: Sousa, S. et al General Performance of Density Functionals . J. Phys. Chem. A 2007, 111, 1043910452 Contracted Gaussian-type orbitals (CGTO) Basis Sets normalization Number of gaussians Variationally optimized Controls width of gaussian L=a+b+c (angular momentum) Why CGTO? 1. Easy to compute with gaussians 2. Gaussians are not accurate enough 3. Linear combination of enough gaussians can approximate a more accurate slater-type orbital Good conceptual explanation: http://vergil.chemistry.gatech.edu/courses/chem6485/pdf/basis-sets.pdf Basis sets • 6-31g* Treatment of Core Orbitals – 6 primitive gaussians per orbital (n = 6) Treatment of valence orbitals each valence orbital is comprised of 2 “orbitals” 1. 2. One composed of 3 primitive gaussians (n=3) One composed of 1 primitive gaussian (n=1) *= addition of d-polarization functions above He • 6-31g** ** = addition of p-polarization functions on H Good conceptual explanation: http://vergil.chemistry.gatech.edu/courses/chem6485/pdf/basis-sets.pdf Example • Carbon atom orbitals – Minimal basis set • 1s, 2s, 2px, 2py, and 2pz orbitals • A total of 5 orbital basis for carbon – 6-31g • 6 gaussians to mimic a 1s • 3 + 1 gaussians to mimic 2s, 2px, 2py, and 2pz EACH – Adding up gaussians: » 4 “valence orbitals” from two CGTOs each • Two CGTO made of 3 GTO and one GTO, respectively • Total of 16 primitive gaussians to describe valence orbitals • Total of 22 primitive gaussians to describe carbon – 6-31g* • Adds 6 d-orbital CGTO to allow polarization of non-H atoms – 6-31g** • Adds 3 p-orbital CGTO to polarize H-atoms Basis sets • cc-pvtz – Correlation consistent – polarized valence triple zeta – Adds extra functions per atom to describe polarization better Atoms cc-pVTZ (from Gaussian H 3s,2p,1d website) He 3s,2p,1d Li-Be 4s,3p,2d,1f B-Ne 4s,3p,2d,1f Na-Ar 5s,4p,2d,1f Ca 6s,5p,3d,1f Sc-Zn 7s,6p,4d,2f,1g Ga-Kr 6s,5p,3d,1f Good conceptual explanation: http://vergil.chemistry.gatech.edu/courses/chem6485/pdf/basis-sets.pdf Molecules of Interest Methylene Top-down Side view Singlet ΔE = 9.09 kcal/mol Triplet Source: Carter, E.; Goddard, W. Electron correlation, basis sets, and the methylene singlet–triplet gap. JCP. 1987, 86, 862-865 Singlet B3LYP/cc-pvtz Methylene SCF E(b3lyp-triplet) = -24,578.5 kcal/mol SCF E(b3lyp-singlet) = -24,566.7 kcal/mol ΔEts = 11.8 kcal/mol -86.464 kcal/mol -155.294 -162.423 -176.604 Triplet Methylene (evaluating accuracy) Computational Results: ΔEts(HF) = 28.43 kcal/mol ΔEts(b3lyp) = 11.8 kcal/mol ΔEts(MP2) = 28.50 kcal/mol Experimental Results: ΔE = 9.09 kcal/mol