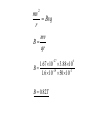* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Answers to Cyclotron Questions File
Path integral formulation wikipedia , lookup
Casimir effect wikipedia , lookup
ALICE experiment wikipedia , lookup
Eigenstate thermalization hypothesis wikipedia , lookup
Large Hadron Collider wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Future Circular Collider wikipedia , lookup
Electron scattering wikipedia , lookup
Nuclear structure wikipedia , lookup
ATLAS experiment wikipedia , lookup
Elementary particle wikipedia , lookup
Compact Muon Solenoid wikipedia , lookup
Atomic nucleus wikipedia , lookup
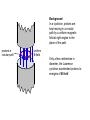
Background In a cyclotron, protons are kept moving in a circular path by a uniform magnetic field at right angles to the plane of the path. protons in circular path uniform B-field Only a few centimetres in diameter, the Lawrence cyclotron accelerated protons to energies of 80 keV. mass of proton = 1.7 x 10–27 kg charge on proton = 1.67 x 10–19 C 1. using so What is the velocity of a proton with an energy of 80 keV? 1 2 KE mv 2 2 80 10 1.6 10 v 27 1.67 10 2E v m Remembering that 1 eV =1.6 x 10-1 9J 80keV = (80 x 103 x 1.6 x10-19) 3 v =3.9 x106ms-1 19 2..The largest possible path had a radius of about 50 mm. What strength of magnetic field must have been used? r =50mm The centripetal force (mv2/r) is provided by the force on the proton due to the magnetic field (BqV) 2 mv F Bqv r r = 50mm ( the path radius ) 2 mv Bvq r mv B qr 27 1.67 10 3.88 10 B 19 3 1.6 10 50 10 B 0.82T 6 3.What would be the radius of the path followed by a proton with half this maximum energy in the same field? Because we know the energy we can calculate the new velocity of the proton. Its energy is half the original so its velocity is. v KE1 2 mv r QB 1.67 1027 3.88 106 r 0.036m 19 3 1.6 10 0.82 10 2 How long would it take 80 keV protons to travel once round their path? How long would it take for those with half this energy? Circular motion theory gives us T 2 and as vr 2 r 2 50 103 8 T 8.1 10 s 6 v 3.88 10 from 3 mv r , r const v QB and T is the same for all velocities and hence all particle energies Constructed of two D -shaped chambers (later called ‘dees’ because of their shape), the cyclotron worked by giving particles of any energy, on their respective paths, a push every time they had completed half an orbit. push push beam of protons 5. How was it possible for particles of differing energy all to be accelerated together? We have just seen that the time taken for an orbit is independent of its energy so particles of different energies will orbit at the same speed e the same mass and chargeprovided that they hav