Download The angular momentum of particle subject to no torque is conserved.

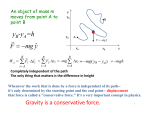
Conservation of Angular Momentum
• Definitions:
Since
Consider
Note
Thus
Conclusion:
r r
Lrp
r r
N r F
r
F  mv&
angular momentum
moment of Force (torque)
r
r
N  r  mv&
d r r
r r r r
L  r  p 
L  r& p  r  p&
dt
r r
r r
r
r  p  r& mv  r& mr& 0
r r& r
Lr pN
r
r&
r
if N=0, then L=0, implies L = constant.
The angular momentum of particle subject to no torque
is conserved.
Work
• Definition (Just a reminder…)
2
r r
W12   Fgdr
1
2
F
r
dr
1
Kinetic Energy
• To motivate the concept, consider:
r r
r
m d 2
m d r r
dv dr
r
dv r
v dt
Fgdr  m g dt  m gvdt 
vgv dt 
2 dt
2 dt
dt dt
dt
r d  mv 2 
Fgdr  
dt

dt  2 
 
The work, W, can thus be expressed as an exact
differential.
2
r r
2 2
1
W12   Fgdr  2 mv  12 m v22  v12
1


 T2  T1
1
Ti  12 mvi2
Definition of Kinetic Energy
Conservative Forces
If the work performed by a force while moving a particle between two
given (arbitrary) positions is independent of the path followed, then the
work can be expressed as a function of the two end points of the path.
2
r r
W12   Fgdr  U1  U 2
1
Conservative
Force or system
• Where we defined the functions Ui as the potential energy of the
particle at the location i.
2
• Note the signs
r r
W12   Fgdr   U 2  U1   U
1
Conservative Forces (cont’d)
• A force is conservative if it can be expressed a the
gradient of a scalar function U.
r
F  gradU  U
Verify by substitution:
2 r
2
r r
r
W12   Fgdr    Ugdr    dU  U1  U 2
2
1
1
1
In most systems of interest,U is a function of the
position only, or position and time. We will study central
potentials in particular, and we will not consider
potentials that depend on velocity.
Conservative Forces (cont’d)
• Important notes about potentials.
– Potentials are defined only up to a
r
r
“constant” since
 U  constant   U
Potentials are known relative to a chosen (arbitrary)
reference.
Choose reference position and values to ease the
solution of specific problems.
E.g. for 1/r potentials, choose U=0 at infinity.
Conservative Forces (cont’d)
• Potential energy is thus NOT an absolute quantity: it
does not have an absolute value.
• Likewise, the Kinetic Energy is also NOT an absolute
quantity: it depends on the specific rest frame used to
measure the velocity.
Total Mechanical Energy
• Definition: E = T + U.
• It is a conserved quantity!
• To verify, consider the time derivative:
Recall
Thus
r
Fgdr  d( 12 mv 2 )  dT
r r
dT Fgdr r r

 Fgv
dt
dt
dE dT dU


dt
dt
dt
The time derivative of the potential can be expressed as
a sum of partial derivatives.
dU
U dxi U


dt
t
i xi dt
Total Mechanical Energy (cont’d)
r
U
U
r& U
dU
U dxi U

x&i 
 U gr 


t
t
dt
t
i xi
i xi dt
 
•
So adding the 2 terms…
r
r r
dE dT dU r r
r U
r U


 Fgv  U gv 
 F  U gv 
dt
dt
dt
t
t
 


=0
Conclusion: if U is not an explicit
function of time, then the energy is
conserved!
dE U
dt

t
Total Mechanical Energy (cont’d)
• In a conservative system, the force can be expressed
as a function of a gradient of a potential independent
of time.
– The total mechanical energy, E, is thus a conserved quantity
in a conservative system.
• The conservations theorem we just saw can be
considered as laws, but keep in mind they strictly
equivalent to Newton’s Eqs 2 & 3.
• Conservations theorems are elegant, and powerful.
– They led W. Pauli (1880-1958) to postulate (in 1930) the
existence of the neutrino, as a product of b-decay to explain
the observed missing momentum!
Example: Mouse on a fan
•
•
Question: A mouse of mass m jumps on the outside of a freely
spinning ceiling fan of moment of inertia I and radius R. By what ratio
does the angular velocity change?
Answer:
– Angular momentum must be conserved.
– Calculate the angular momentum before and after the jump.
– Equate them.
I 
I
before
Lbefore  I before before
Lafter  I after after
Lafter  Lbefore
 after I before
I


 before I after I  mR 2
before
 after
after
 after I before

 before I after
Energy
• Concept of energy now more popular than in
Newton’s time…
• Became clear early 19th century that other
forms of energy exist: e.g. heat.
• Rutherford discovered clear link between
heat generation and friction.
• Law of conservation of energy first formulated
by Hermann von Helmholtz (1821-1894)
based on experimental work done largely by
James Prescott Joule (1818-1889).
Use of Energy for problem solving.
• Total mechanical energy:
1-D Case:
v(x) 
E  T  U  12 mv 2  U(x)
dx
2

E  U(x)
dt
m
x
t  to 

xo
dx
2
E  U(x)
m
with x=x o
This is a “generic” solution: need U(x) and integrate
to get a function of t(x)...
Energy (cont’d)
•
•
Can learn a great deal without performing the integration (which can
get difficult…).
Consider a plot of the energy and potential vs x.
T  12 mv 2  0
E4
E3

E  U(x) for any real solution.
E=E4 - unbound motion
E=E3 - 1 side bound, non periodic
E2
E=E2 - bound periodic motion
E1
E=E1 - bound periodic motion
E0
x
Energy (cont’d)
• Note: Whenever motion is restricted near a minimum of a
potential, it may be sufficient to approximate U(x) with a
harmonic potential approximation
U(x)  12 k(x  xo )2
U(x)
E
Stable/Unstable equilibrium
•
One can determine whether an equilibrium is stable or unstable base
on the curvature of the potential at the equilibrium point.
U(x)
U(x)
E
E
unstable
stable
Consider a Taylor expension of the potential:
x 2  2U(x) 
x 3   3U(x) 
 U(x) 
U(x)  U(xo )  x 

 
L
 x  x  xo 2!  x 2  x  x
3!  x 3  x  x
o
o
Stable/Unstable equilibrium (cont’d)
• We have an equilibrium if:
Near xo:
 dU(x) 

  0
dx xo
x 2   2U(x) 
x 3   3U(x) 
U(x)  U(xo )  
 
L
2
3


2!  x  x  x
3!  x  x  x
o
o
Stable equilibrium if:
  2U(x) 
0
 x 2 
x  xo
Unstable equilibrium if:
  2U(x) 
0
 x 2 
x  xo
Higher orders to be considered if:
  2U(x) 
0
 x 2 
x  xo