Download electric potential

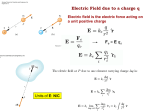
Chapter 25
Electric Potential
Electrical Potential Energy

When a test charge is placed in an electric field, it
experiences a force
 F  q E
o



The force is conservative
If the test charge is moved in the field by some
external agent, the work done by the field is the
negative of the work done by the external agent
ds is an infinitesimal displacement vector that is
oriented tangent to a path through space
Electric Potential Energy, cont

The work done by the electric field is
F  ds  qoE  ds

As this work is done by the field, the potential
energy of the charge-field system is changed
by ΔU = qoE  ds
For a finite displacement of the charge from A
to B,

 
B 

ΔU  U B  U A   F  ds  q0  E  ds
B
A
A
Potential Energy
 

GMm
ΔU  U  U    F  d s    (
r̂)  d s
r
B
A
B
B
A
A
2

r
GMm
U  U (r )  
r
 
B 

ΔU  U B  U A   F  ds   mg  ds
B
A
y
A
U  U ( y )  mgy

g
 
B 

ΔU  U B  U A   F  ds   kx  ds
B
A
U  U ( x) 
1 2
kx
2
A
 
B 

ΔU  U B  U A   F  ds  q0  E  ds
B
A
A
U  U (r )  ?
Electric Potential

The potential energy per unit charge, U/qo, is
the electric potential

The potential is characteristic of the field only




The potential energy is characteristic of the charge-field
system
The potential is independent of the value of qo
The potential has a value at every point in an
electric field
The electric potential is
B
B 


ΔU  U B  U A   F  ds  q0  E  ds
A
A
U
V
qo
Electric Potential, cont.

The potential is a scalar quantity


Since energy is a scalar
As a charged particle moves in an electric
field, it will experience a change in potential
B 

ΔU U B U A


  E  ds
A
q0
q0 q0
B
U
V 
   E  ds
A
qo
 
ΔV  VB  VA   E  ds
B
A
Potential Difference in a
Uniform Field

The equations for electric potential can be
simplified if the electric field is uniform:
B
B
A
A
VB  VA  V   E  ds  E  ds  Ed

The negative sign indicates that the electric
potential at point B is lower than at point A

Electric field lines always point in the direction of
decreasing electric potential
Energy and the Direction of
Electric Field



When the electric field is
directed downward, point
B is at a lower potential
than point A
When a positive test
charge moves from A to
B, the charge-field
system loses potential
energy
Uniform Field
Use the active figure to
compare the motion in
the electric field to the
motion in a gravitational
field
B
B
VB  VA  V   E  ds  E  ds  Ed
A
A
VA  VB
PLAY
ACTIVE FIGURE
More About Directions

A system consisting of a positive charge and an
electric field loses electric potential energy when the
charge moves in the direction of the field


An electric field does work on a positive charge when the
charge moves in the direction of the electric field
The charged particle gains kinetic energy equal to
the potential energy lost by the charge-field system

Another example of Conservation of Energy
예제25-1

E?
=3mm
ΔV
12V
E

 4000V / m
d
0.003m
Fig. 25-5, p. 696
Charged Particle in a Uniform
Field, Example
예제25-2
A positive charge is
released from rest and
moves in the direction of the
electric field
 The change in potential is
negative
 The change in potential
energy is negative
 The force and acceleration
are in the direction of the
field
 Conservation of Energy can
be used to find its speed
ΔE  ΔU  ΔK  0,

=0.5m
ΔU  qΔV  -qEd, ΔK  mv2 /2
v  2qEd/m  2 1.6 10 19  8 10 4  0.5  2.8 106 m / s
8x104V/m=
Potential and Point Charges

kq r  kq
kq
 ds  2 ds cos   2 dr
 A positive point charge r 2
r
r

produces a field
directed radially
outward
The potential difference
between points A and B
will be

B 
B

kqr 
VB  VA    E  ds    2  ds
A
A r
B kq
1 1
   2 dr  kq  
A r
 rB rA 
VA  VB : q  0
 1 1
VB  VA  keq   
kq r
 B rA 
V  V (r ) 
r
Potential and Point Charges,
cont.



The electric potential is independent of the
path between points A and B
It is customary to choose a reference
potential of V = 0 at rA = ∞
Then the potential at some point r is
kq
V  V (r ) 
r
V  V (r )  V (r )  V ()  V
V ()  0 ; rA  ref  
Potential Energy of Multiple
Charges


Consider two charged
particles
The potential energy of
the system is
q1q2
U  ke
r12

Use the active figure to
move the charge and see
the effect on the potential
energy of the system
PLAY
ACTIVE FIGURE
U with Multiple Charges, final


If there are more than
two charges, then find
U for each pair of
charges and add them
For three charges:
 q1q2 q1q3 q2q3 
U  ke 



r
r
r
13
23 
 12

The result is independent
of the order of the
charges
예제25-3

q1
q2
VP  k  k
r1
r2
6
9 2
 9 10 (  ) 106
4 5
 6300(V)
에너지 변화
ΔU  q3 ΔV  q3(VP  V )  q3VP
 3  10 6  (6300)
 0.0189(J)
예제 25.3 두 점 전하에 의한 전위
q1=2.00μC의 점 전하가 원점에 놓여 있고, q2=-6.00μC의 전하가 y축 위의 (0, 3.00)m에 놓여 있다.
(A) 좌표가 (4.00, 0)m인 점 P에서 이 들 두 전하에 의한 전체 전위를 구하라.
(B) q3=3.00μC의 전하를 무한대에서 점 P까지 가져옴에 따라 세 전하로 이루어지는 계의 전체 위치
에너지 변화를 구하라.
풀이
 q1 q2 
 
 r1 r2 
(A) V p  ke 

V p  (8.99  109 N  m 2 / c 2 )
 2.00  10 6 C 6.00  10 6 C 



4
.
00
m
5
.
00
m


 6.29 103V
(B)
U f  q3V p
U  U f  U i  q3V p  0
 (3.00 10 6 C )( 6.29 103V )
 1.89 10  2 J
Finding E From V

Assume, to start, that the field has only an x
component
B

V

V


E

d
s
B
A

dV
Ex  


A
 dV   Eds  E  dV / ds
Similar statements would apply to the y and z
components
Equipotential surfaces must always be
perpendicular to the electric field lines passing
through them
dx
E and V for a Dipole



The equipotential lines
are the dashed blue
lines
The electric field lines
are the brown lines
The equipotential lines
are everywhere
perpendicular to the
field lines
예제25-4
VP  0
VR  k
2kqa
x ; V  2
x
Ex  
-q
q
2kqa
k
 2
x-a
xa
x  a2
dV
d  2kqa 
4kqa
   2    3
dx
dx  x 
x
예제 25.4 쌍극자에 의한 전위
전기 쌍극자는 2a의 거리만큼 떨어져 있는, 전하의 크기는 같고 부호가 반대인 두 개의 전하로
이루어져 있다. 이 쌍극자는 x축 상에 있고, 그 중심은 원점에 있다. (A) y축 상의 점 P에서의 전위를
구하라. (B) ＋x축 상의 점 R에서의 전위를 구하라. (C) 쌍극자로부터 멀리 떨어져있는 곳에서의 V와
Ex를 구하라.
풀이
 q

q

q
i
(A) V p  ke   ke 

0
2
2
2
2
i ri
 a  y
a  y 
(B)
VR  ke 
i
(C)
qi
2k qa
q 
 q
 ke 

 2 e 2
ri
x a
 xa xa
2k qa
 2k qa 
VR  lim   2 e 2    e2
( x a)
x
x  a  x  a 
Ex  
4k qa
dV
d  2k qa 
d 1
    e2   2ke qa  2    e2
( x a)
dx
dx  x 
dx  x 
x
V for a Continuous Charge
Distribution, cont.

To find the total potential, you need to
integrate to include the contributions from all
the elements
dq
1 V  ke 
r

This value for V uses the reference of V = 0 when
P is infinitely far away from the charge
distributions
V From a Known E

If the electric field is already known from
other considerations, the potential can be
calculated using the original approach
B
V   E  ds
2
A

If the charge distribution has sufficient symmetry,
first find the field from Gauss’ Law and then find
the potential difference between any two points

Choose V = 0 at some convenient point
V for a Uniformly Charged
Ring
예제25-5

P is located on the
perpendicular central
axis of the uniformly
charged ring

The ring has a radius a
and a total charge Q
keQ
dq
V  ke 

r
a2  x 2
예제 25.5 균일하게 대전된 고리에 의한 전위
(A) 반지름이 a인 고리에 전체 전하량 Q가 고르게 분포하고 있을 때, 중심축 상의 한 점 P에서
전위를 구하라.
풀이
(A) V  ke

dq
dq

k
 r e  a2  x2
ke
a2  x2
keQ
 dq 
a2  x2
(A) 반지름이 a인 고리에 전체 전하량 Q가 고르게 분포하고 있을 때, 중심축 상의 한 점 P에서
전기장을 구하라.
풀이
dV
d
 keQ
(a 2  x 2 ) 1/ 2
dx
dx
3 / 2
 1
  k e Q   a 2  x 2
(2 x)
 2
(B) E x  


Ex 
ke x
Q
2
2 3/ 2
(a  x )
V for a Uniformly Charged Disk


The ring has a radius R
and surface charge
density of σ
P is along the
perpendicular central
axis of the disk

V  2πkeσ  R 2  x 2


R
k edq
0
r x
V 
2
2

R
0

1
2

 x

k e 2 rdr
r 2  x2
예제25-6
dq  dA  2rdr
예제 25.6 균일하게 대전된 원반에 의한 전위
반지름이 R이고 표면 전하 밀도가 σ인 균일하게 대전된 원반이 있다. (A) 원반의 중심축 상의 한 점
P에서의 전위를 구하라. (B) 점 P에서의 전기장의 x 성분을 구하라.
풀이
(A) dq  dA   (2r dr )  2r dr이므로
dV 
ke dq
r x
2
2

ke 2rdr
r 2  x2
R
2r dr
0
r 2  x2
V  ke 
R
 ke  (r 2  x 2 ) 1/ 2 2r dr
0

V  2ke ( R 2  x 2 )1/ 2  x
(B)
Ex  



dV
x
 2ke 1  2 2 1/ 2 
dx
 (R  x ) 
V for a Finite Line of Charge

A rod of line ℓ has a
total charge of Q and a
linear charge density of
λ
V
keQ
  a2 
ln 

a

2




예제25-7
예제 25.7 선 전하에 의한 전위
x축 상에 놓여있는 길이가 인 막대가 있다. 전체 전하량이 Q인 이 막대는 선
전하 밀도 λ=Q/ℓ로 균일하게 대전되어 있다. 원점에서 거리가 a 만큼 떨어진 점
P에서의 전위를 구하라.
풀이
dq  dx
dV  ke
dq
dx
 ke
이므로
2
2
r
a x
dx

V   ke
a2  x2
0
 ke  

0

dx
a2  x 2
 ke

Q
ln x  a 2  x 2

Q
ln (   a 2   2 )  ln a

Q    a2  2 
 ke ln 

 
a

 ke



0
V Due to a Charged Conductor




Consider two points on the
surface of the charged
conductor as shown
E is always perpendicular to
the displacement ds
Therefore, E  ds  0
Therefore, the potential
difference between A and B
is also zero
B
2
V   E  ds = 0
A
E Compared to V
The electric potential is a
function of r
 The electric field is a
function of r2
 The effect of a charge on
the space surrounding it:
 The charge sets up a
vector electric field which
is related to the force
 The charge sets up a
scalar potential which is
related to the energy
2

r 
r kqr


 1 1  kq
r  R : Vr  V    E  d s    2  d s kq   

 r
r  r

r 
R kqr

 r

 1 1  kq
r  R : Vr  V    E  d s    2  d s   0  d s  kq   

 r
R
R  R

예제25-8
V k
E1  ? E2  ? at surfaces
q1
q
q
r
k 2  1  1
r1
r2
q2 r2
q1
q2
E1  k 2 , E2  k 2
r1
r2
E1 q1 r22 r2

  1  E1  E2
2
E2 q2 r1
r1
E2

V1  V2  V
in electrostatic equilibriu m
E1
Fig. 25-20, p. 708
Cavity in a Conductor, cont


The electric field inside does not depend on the
charge distribution on the outside surface of the
conductor
For all paths between A and B,
B
VB  VA   E  ds  0
A

A cavity surrounded by conducting walls is a fieldfree region as long as no charges are inside the
cavity