* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Class Notes 2 - Graphing and Writing Absolute Value Functions
Survey
Document related concepts
Transcript
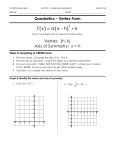
Graph and Write Absolute Value Equations f ( x) x What are the key attributes of a Function and define? Key attributes: Domain: Range: Intercepts: Symmetry: Minimum: Graph the absolute value parent function (2A.2A) First we will us a table to graph the absolute value linear parent function. Consider all real numbers. f ( x) x Let’s Discuss the Table Example: Input x Process: Output f(x) -8 8 8 What would happen if the input was not an integer? 1 2 What decisions can you make from the pattern you discovered? What would this look like on a graph? 3 1 2 3 1 2 3 0 0 0 -122.96 122.96 122.96 Set Notation and Interval Notation in relation to Domain and Range: Inequality/ Previous notation All real numbers x0 x -2 -1 0 1 2 f(x) 2 1 0 1 2 Set notation Interval notation Read “All numbers x such that x belongs to the set of real numbers” “from negative infinity to positive infinity” Read “all numbers x such that x is greater than or equal to 0” “from 0 to positive infinity, including 0” x x x x 0 Parent Graph: f x x , 0, Key attributes: Domain: Range: Intercepts: Symmetry: Minimum: How is this like something you have done before? How is the absolute value graph similar and different to the quadratic? 1 How is the absolute value graph similar and different to the linear? Table x y 1 4 2 2 3 0 Graph 6 2 f x 3 x 2 1 7 4 What is the minimum value of this absolute value function? What is the maximum value on the interval, 1,5 ? Equation What is the axis of symmetry? What is the domain of this absolute value function? What are the x-intercepts? What is the range? What is the minimum value on the interval 9,5 ? You Try1 Using the graph on the side answer the questions below: What is the minimum value? ________________ What is the axis of symmetry? _______________ What are the x-intercepts? __________________ What is the domain? _______________________ What is the range? _________________________ What is the y-intercept? _____________________ You Try 2 Using the graph to answer the questions below: What is the minimum value? ________________ What is the axis of symmetry? _______________ What are the x-intercepts? __________________ What is the domain? _______________________ What is the range? _________________________ What is the y-intercept? _____________________ 2 What is the y-intercept? Class Activity Open the TI-Nspire document Exploring AbsoluteValue Transformations Press / ¢ to move to page 1.2 and begin the lesson 1. Write the vertex form of an absolute value function. _______________________________. Note in this activity b is always assumed to be 1 2. Observe the characteristics of the absolute value parent function on page 1.2. List the characteristics observed: ________________________________________ Exploring “a.” 3. Increase and decrease the value of “a.” Describe what is happening to the function. __________________________________________________________________________________________________ __________________________________________________________________________________________________ __________________________________________________________________________________________________ 4. Complete the statements below. When “a” positive, the function____________________________________________________ _____________________________________________________________________________. Therefore, when “a” is positive, the function has a ____________________________________. (Maximum or Minimum) When “a” negative, the function ___________________________________________________ _____________________________________________________________________________. Therefore, when “a” is negative, the function has a ____________________________________. (Maximum or Minimum) 5. What happens when a = 0 and -1 < a < 1? _________________________________________ _____________________________________________________________________________. 3 Exploring “h.” 6. Increase and decrease the value of “h.” Describe what is happening to the function. The function moves _____________________________________________________________. 7. Complete the statements below. When “h” is positive, the function____________________________________________________. When “h” is negative, the function ___________________________________________________. Exploring “k.” 8. Increase and decrease the value of “k.” Describe what is happening to the function. The function moves_____________________________________________________________. 9. Complete the statements below. When “k” positive, the function ___________________________________________________. When “k” negative, the function ___________________________________________________. 10. Use your TI-Nspire to discover how to find the Vertex? Fill in the chart: Parameters: a = 1 h=0 k=0 This is called the parent functions. Vertex form: y 1 x 0 0 Simplify Parameters: a = .5 h = -3 k=0 Parameters: a = 2 h=1 k = 2.5 1 3 h = -2.3 k = -1.5 Parameters: a = - y x Identify the coordinates of the minimum. ( , ) How did the function move? Vertex form: Identify the coordinates of the minimum. ( , ) How did the function move? Vertex form: Identify the coordinates of the minimum. ( , ) How did the function move? Vertex form: Identify the coordinates of the minimum. ( , ) 4 Vertical Dilation: f x a x Explore the difference between a vertical stretch and a vertical compression. Discover: a > 1 results in a ________ stretch (graph gets ________________ ) 0 a 1results in a _____________ compression (graph gets ___________) What characteristic of the graph does “a” also seem to describe? It seems that “a” defines the ______________ of the right leg of the graph Horizontal Dilation: f x bx Explore the difference between a horizontal stretch and a horizontal compression. Discover: b 1results in a _____________ compression (graph gets ___________) 0 b 1 results in a ________stretch (graph gets ___________) Is there another way you could write the equation of this graph if the value of “b” was set equal to 1? It seems that value of __________ can be moved outside the | 5 | and set the the value of _____________ Reflections: f x x versus f x x Explore Horizontal and Vertical reflections. What would happen if a was negative? What would happen if b was negative? Discover: a 0 results in a reflection over the ___-axis (graph opens down) b 0 results in a reflection over the ___-axis (graph looks the same due to symmetry) Think-Pair-Share Activity How is the result of f x x similar to something you have done before? Why does there appear to be no change with f x x when compared to f x x ? This must mean that if the value “b” is brought outside the | setting it equal to “a” | we must first take its _______ value before Horizontal Translation: f x x h Explore the horizontal shifts using positive and negative values for h. Discover: h 0 results in a ______ to the ____ (the sign remains negative) h 0 results in a ____ to the ____ (the sign becomes positive) What do you notice about the horizontal translation and the sign? 6 Vertical Translation: f x k Explore the vertical shifts using positive and negative values for k. Discover: k 0 results in a _______shift ___ (the sign is ___________) k 0 results in a _______ shift ___ (the sign is ___________) I Do Example: Inequality f x 2 x 1 5 Domain Describe the transformation: a: ____________________________ b: ____________________________ h: ____________________________ k: ____________________________ Range Identify the Key Attributes: 7 Set notation Interval notation We Do: x 3 7 Describe the transformation: a: ____________________________ b: ____________________________ h: ____________________________ k: ____________________________ You do 1: y 2 x 6 5 Describe the transformation and Idenitfy the key attributes of the function. Transforms 1) _______________________ 2) _______________________ 3) __________________________ Identify the Key Attributes: _____________________________ _____________________________ _____________________________ 8 You do 2: f ( x) x 2 4 Describe the transformation and Idenitfy the key attributes of the function. Transforms 1) _______________________ 2) _______________________ 3) __________________________ Identify the Key Attributes: _____________________________ _____________________________ _____________________________ You do 3: f ( x) x 2 1 Describe the transformation and Idenitfy the key attributes of the function. Transforms 1) _______________________ 2) _______________________ 3) __________________________ Identify the Key Attributes: _____________________________ _____________________________ _____________________________ Key attributes based on the Vertex: Which transformations affect domain? Which transformations affect range? Which transformations affect the axis of symmetry? 9 Which transformations affect whether the graph has a maximum or a minimum? How can the maximum or minimum be determined from the equation? Solve for x-intercepts and y-intercepts How can we verify the y-int. algebraically? What does a y-int. mean? Notice from the graph of f x 2 x 1 5 above, it has a y-intercept at __________? f 0 2 0 1 5 Let 2 1 5 x 0 and evaluate 21 5 7 Notice that the graph of f x 2 x 1 5 does not cross the ____-axis so when solving algebraically we should get __. 2 x 1 5 0 Let y 0 and solve 2 x 1 5 x 1 Notice the absolute value is negative so there is no solution. 5 2 What do we notice about the graph and x-intercepts? Explain the relationship between the algebraic and graphic method for finding intercepts. You Try: Determine the min/max, x&y intercepts: 𝟏 𝟐 1. Y = -|x+4| + 4 2. Y = |x-2| + 4 10 Graph absolute value with transformations (2A.6C): f x a b( x h) k WHAT HAPPENS WHEN B DOES NOT EQUAL 1 ? Are the b and h variables easily identifiable in the equation below? What are the transformations? f x 3x 6 What is the vertex? What is the axis of symmetry? How can we make b and c easily identifiable? How is it related to the quadratic with the same transformations? IN ORDER TO DETERMINE h FOR VALUES OF B ≠ 1 YOU MUST PUT THE ABSOULTE VALUE EQUATION INTO VERTEX FORM: f(x) = a|b(x-h)| + k vertex form for absolute value Step 1: Put parentheses around the argument: f x (3x 6) 2 f x 3( x 2) 2 Step 2: Factor out b from the parentheses: or f(x) = 3|x+2| +2 We Do: Determine the x & y intercepts, the horizontal & vertical shifts and the min or max of the function: f(x) = -2|4x -12| + 3 y intercept = f(0) = ______________________ x intercept(s) by solving 0 = ____________________ Vertical shift = k = _______________________ Horizontal shift = h f(x) = -___|___(x-____)| + 3 Or f(x) = _______________________ Min or Max occurs at the vertex = (h,k) = (_____,_____) if a is negative then the vertex is a ________________ Axis of symmetry: x = ___________________________ 11 You Try: Determine the x & y intercepts, the horizontal & vertical shifts and the min or max of the function: f(x) = 2|3x + 9| -4 y intercept = f(0) = ______________________ x intercept(s) by solving 0 = ____________________ Vertical shift = k = _______________________ Horizontal shift = h f(x) = -|___(x-____)| - ______ Min or Max occurs at the vertex = (h,k) = (_____,_____) if a is _________ then the vertex is a ________________ Axis of symmetry: x = ___________________________ Graph the function: 12 Practice Problems I. For each equation: state the transformations, domain, range and intercepts and graph the equation. 1 x 3 2 1) y x 4 5 2) f ( x ) Trans: Trans: Trans: D: _______ R:________ x-int:________________ y-int:________________ Axis of sym:__________ D: _______ R:________ x-int:________________ y-int:________________ Axis of sym:__________ D: _______ R:________ x-int:________________ y-int:________________ Axis of sym:__________ 5) y x 3 6 6) f ( x) 2 x 1 3 Trans: Trans: Trans: D: _______ R:________ x-int:________________ y-int:________________ Axis of sym:__________ D: _______ R:________ x-int:________________ y-int:________________ Axis of sym:__________ D: _______ R:________ x-int:________________ y-int:________________ Axis of sym:__________ 4) f ( x ) 1 x3 2 3) y 2 x 10 1 13 14 Writing equations from a graph: How is the graph different from the parent? Which transformations would cause each change? Opens down (___________), Slope of 2 (__________), vertex at ______ (moves ______ 3 and ____ 4) How can we represent the changes in an equation? f x 2 x 3 4 or f x 2x 3 4 or f x 2 x 6 4 How would the graph of a quadratic look with the same transformations? What is the linear equation of each “piece” of the graph? How do the linear equations relate to the absolute value equation? Steps in developing equations from Graphs: (This applies to any function we will study): 1. Identify the function type and graph its parent function. In our case f(x) = |x| 2. Compare the function graph with the parent function graph and list the transforms that are apparent: - Magnitude of the slope of the branches? This will be the “a” value - Reflection across the x axis: Yes, we negate “a” - How has the x coordinate of the vertex changed from the parent (size & direction) this will be “h” - -How has the y coordinate of the vertex changed from the parent (size & direction) this will be “k” 3. Plug in the values of a, h, and k into the vertex form of the function f(x) = a|b(x-h)| + k Note: b will always be 1 with this process 15 Example We Do: Determine the equation that defines the graph below: Step1: The graph above is a transform of the parent function f(x) = ________________ Step 2. Magnitude of the slope of the branches = _______________ so “a” seems to be ______________ Step 3: Relection on x? _____________ so the sign of “a” _________ change so “a” = ____________ Apparent horizontal shift = _____________ to the ____________ so h = _____________ Apparent verical shift = _____________ ____________ so k = _____________ Step 4: The f(x) = ____(x - ________) + _________ You Do: Determine the equation that defines the graph below: Step1: The graph above is a transform of the parent function f(x) = ________________ Step 2. Magnitude of the slope of the branches = _______________ so “a” seems to be ______________ Step 3: Reflection on x? _____________ so the sign of “a” _________ and “a” = ________________ Apparent horizontal shift = _____________ to the ____________ so h = _____________ Apparent vertical shift = _____________ ____________ so k = _____________ Step 4: The f(x) = ____|x - ________| + _________ You Do: Determine the equation that defines the graph below: Step1: The graph above is a transform of the parent function f(x) = ________________ Step 2. Magnitude of the slope of the branches = _______________ so “a” seems to be ______________ Step 3: Relection on x? _____________ so the sign of “a” _________ and “a” = ________________ Apparent horizontal shift = _____________ to the ____________ so h = _____________ Apparent verical shift = _____________ ____________ so k = _____________ Step 4: The f(x) = ____|x - ________| + _________ 16 17 Practice Problems: Determine the equation for the following graphs when b = 1 and an equivalent equation when b≠1: Verify you answer by graphing on the Nspire. A B C D 18