Download . q q F k d =

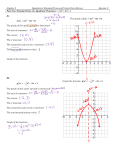
Algebra 1 Review for Chapter 1 Test
In exercises 1 – 4, solve each equation. Check your answer(s).
1.  a  2  9  6
3.
2. 3 4  3m  30
 4 5g  12  12
4. x  3  9  30
5. A thermometer comes with a guarantee that the displayed temperature differs from the actual
temperature by no more than 1.5 degrees Fahrenheit. Write and solve an equation to find the minimum
and maximum actual temperatures when the thermometer displays 54.5 degrees Fahrenheit.
6. A machine fills bags with 16 ounces of sugar. Each bag must be filled to within 0.3 ounce of the required amount.
Write and solve an equation to find the minimum and maximum weight that the bags can be filled.
7. For a school play, the maximum age for a youth ticket is 18 years old. The minimum age is 10 years old. Write an
absolute value equation for which the two solutions are the minimum and maximum ages for a youth ticket.
8. Safety regulations require a guard rail to have a minimum height of 28 inches and a maximum height of 40 inches.
Write an absolute value equation that represents the possible heights of a guard rail.
In Exercises 9-14, solve the equation. Check your solutions.
9. x  2  3x
10.
12. 3 3t  1  2 6t  3
13. 3 w  5  2w  10
6 x  16  2 x
11.
z 4  z 6
14. 2k  4  2k  3
15. Your friend says the absolute value equation 2 x  9  7  3 has two solutions because the constant on the
right side of the equation is positive. Is your friend correct? Explain.
In Exercises 16-18, solve the literal equation for y.
16. 12 x  3 y  15
18. 4  2 y  10  6 x
17. 14  7 y  21
3
In Exercises 19-21, solve the literal equation for x.
19. y  3x  6 x
21. ux  rx  w
20. m  9 x  x
22. Describe and correct the error in solving the equation for x.
23. Coulomb's Law is given by the formula F  k
q1q2
.
d2
The force F between two charges q1 and q2 in a vacuum is proportional to the product of the
charges, and is inversely proportional to the square of the distance d between the two charges.
Solve the formula for k.
24. Solve the diamond problems below.
prod uct
#
#
sum
-2
-9
-1
1.5
-4.5
7
4
26. Describe this graph completely.
25. Draw a complete graph for 𝑦 = −√𝑥 + 1 and
then describe the graph completely.
y
x
27. Describe how the graph of 𝑦 = −√𝑥 + 1 and the graph of 𝑦 = √𝑥 are similar and different.
28. Solve each of the following equations for x.
a. 3𝑥 + 2 = 𝑥 − 8
b. −2(5𝑥 + 3) = 6𝑥 − 30
c. 3(𝑥 + 4) − 2(𝑥 − 3) = −4 + 𝑥
d. − 4 𝑥 − 4 = −20
3
29. If 𝑓(𝑥) = −2𝑥 2 − 3𝑥 + 2 calculate the following:
a. f (3)
b.
f (2)
1
4
f( )
c.
30. For each relation, find the missing inputs or outputs. If no input or output is possible, explain why not.
a.
b.
x = -1
x = –2
√𝑥 +1
-3x+10
c.
d.
-2
x=
x = –2-9
𝑥2
3
− √𝑥 + 1
31. For f (x)  2x  8 , determine the following.
a. f(-4)
b. f(x) = 9
32. For f(x) = |𝑥 + 3| determine the following.
a. f (2)
b. f (x)=16
3
33. For f(x) = √3𝑥 −1, determine the following.
a. f(9)
b. f(x) = 2
34. Compare the graphs. Find the value of k.
Answers:
14
1. No solution
2. m = – 2,
3
5. |𝑥 − 54.5| = 1.5; 53, 56
8. 𝑦 = |𝑥 − 34| = 6
9. x = 1
3
12. t = – 1, − 7
13. w = 1, 5
3. y = 3,
9
5
6. |𝑥 − 16| = 0.3; 16.3, 15.7
10. x = 2, 4
7
14. k = − 4 (4 ≠ 3)
4. x = 24, – 18
7. 𝑦 = |𝑥 − 14| = 4
11. z = – 1 (−4 ≠ 6)
15. No. You can’t determine the number of solutions until the absolute value is isolated. In this case, the value on
the right would be – 4, so there is no solution.
16. 𝑦 = −4𝑥 − 5
17. y = – 1
18. 𝑦 = 9𝑥 − 9
𝑦
𝑚
𝑤
19. 𝑥 = 9
20. 𝑥 = 8
21. 𝑥 = 𝑢+𝑟
22. You can’t factor out an x in step one because it is not in every term (d).
𝑘−𝑑
=𝑥
𝑎+𝑏
2
𝑑
23. 𝑘 = 𝐹 (𝑞 𝑞 )
1 2
24.
25. - As x increases, y decreases
- Special points: Vertex (– 1, 0) (also x-int), y-int (0, – 1)
- No symmetry
- Gradual curve
- No input less than – 1, no output greater than 0
26. – U-shaped, opens upward
- Minimum (vertex) (1, – 10)
- When x is less than 1, y is decreasing. When x is greater
than 1, y is increasing
- Symmetrical at 𝑥 = 1
- Any input, output greater than or equal to – 10
- x-intercepts ≈ (−1, 0) and (3, 0), y-intercept (1, – 8)
27. Similar: both are square root functions and are curved. Neither has symmetry.
Different: Vertex for #25 is (-1, 0), vertex for parent function is (0, 0)
#25 is a reflection in the x-axis from the parent function
#25 has a y-intercept of (0, -1), parent function has x- and y-intercepts at the origin
#25 as x increases, y decreases. Opposite for the parent function
#25 input is greater or equal to -1. Parent function has input greater or equal to 0
#25 has output less than or equal to 0. Parent function has output greater than or equal to 0.
28. a. x = – 5
b. x = 1.5
c. No solution
29. a. – 25
b. 0
c. 18
30. a. Not possible, can’t square root a negative.
31. a. Not possible
b. x = 45
32. a. 1
b. x = 13 or – 9
33. a. 2
b. x = 9
34. k = 3
1
b. x = 4
1
d. x = 213
c. 𝑥 = √8 𝑜𝑟 − √8
d. 2