Download Quantum Numbers

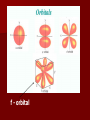
The Quantum Model of
the Atom
Honors Chemistry
Louie de Broglie

Proposed that all particles of matter that
move exhibit wave like behavior (even a
baseball!)

He came up with the following equation that
relates the wavelength of a particle to its
mass and velocity. (Derived from E=mc2 and
E = hc/)

=
h_
mv
 Using the mass of an electron moving at the
speed of light, he calculated the same energy
level values as Bohr did for the Hydrogen atom.
Louis de Broglie

De Broglie realized that the
electrons exhibit wavelike
properties in their quantized
orbits. (draw pictures )
He said that if an electron has
wavelike motion and is
restricted to circular orbits of
a fixed radius, the electron
is allowed only certain
possible wavelengths,
frequencies and energies.
 Experiments did show that
electrons in atoms do exhibit
wave behavior with specific
frequencies.

The Heisenberg Uncertainty Principle
Heisenberg concluded that it is impossible to make
any measurement on an object without disturbing
it – at least a little.
 Electrons are detected by photons and because a
photon and an electron have the same energy,
any attempt to locate an electron with a photon
will knock the electron off course.
 Therefore:
It is impossible to know both the
position and the velocity of an electron at
the same time.



So we can only talk about the probability of
finding and electron in certain area (remember the
fuzzy cloud!)
Erwin Schrodinger

Used the idea that electrons behave like
waves to write and solve a mathematical
equation to describe the location and energy
of an electron in the hydrogen atom.

The modern description of the electron
cloud in atoms comes from the solutions to
the Schrodinger equation.

This equation showed that the energy of
electrons are restricted to certain
values.
Erwin Schrodinger
However, the equation does not define
the exact path the electron takes
around the nucleus.
 It only estimates the probability of
finding an electron in a certain position,
unlike Bohr’s circular orbits.

Electrons exist in regions called Orbitals
 Orbital – 3 dimensional cloud shape
around the nucleus that indicates the
probable location of an electron

Atomic Orbitals
The
solutions to the
Schrodinger equation are
called Quantum Numbers,
and they are used to describe
the properties, such as the
energy level and shape, of the
atomic orbitals.
“s” - orbital
“p” orbitals
“d” orbitals
f - orbital
Quantum Number Information

Definition: Set of 4 numbers that tells
us the probable location of the electron.
It is like a zip code for the electron
 The numbers tell us the energy level,
shape and orientation of the orbital
 And, it tells us the spin direction of the
electron in that orbital

Quantum Number Information
Name
Definition
Symbol
Assigned Value
Principle
Quantum
Number
Indicates the main
energy level occupied
by the electron
Secondary
Quantum
Number
Indicates the shape of
the orbital occupied by
the electron
Magnetic
Quantum
Number
Spin
Quantum
Number
Indicates the orientation
of the orbital around the
nucleus
m
If l = 1
Then m = -1, 0 , +1
Indicates the spin
direction of the
electron.
s
+½ or -½
n
l
n = 1, 2, 3, . . . 7. .
l
l
l
l
= 0 to (n-1)
= 0 “s” orbital
= 1 “p” orbital
= 2 “d” orbital
m = -l to +l
Only 2 electrons are allowed in each
orbital
 Each with an opposite spin.
 Given the following quantum numbers,
describe the “probable” location of the
electron.
 n, l, m, s,
 2, 1, 0, + ½
 The electron is in energy level 2
 It is in a “p” orbital
 The orientation of the orbital is the y-axis

Quantum # and Atomic Structure
Main
Energy
Level (n)
Sublevels
(n)
*Orbital
shapes
# of
orbitals
per
sublevel
1
s
2
s
p
1
3
3
s
p
d
1
3
5
4
s
p
d
f
1
3
5
7
1
# orbitals
per main
energy
level (n2)
# of
electrons
per
sublevel
Total # of
electrons
per main
energy
level (2n2)
1
2
2
4
s= 2
p= 6
8
9
s= 2
p=6
d = 10
18
16
s=2
p=6
d = 10
f = 14
32