Download practical stability boundary

Motif Refinement using Hybrid
Expectation Maximization Algorithm
Chandan Reddy
Yao-Chung Weng
Hsiao-Dong Chiang
School of Electrical and Computer Engr.
Cornell University, Ithaca, NY - 14853.
Motif Finding Problem

Motifs are certain patterns in DNA and protein sequences that are
strongly conserved i.e. they have important biological functions like
gene regulation and gene interaction

Finding these conserved patterns might be very useful for
controlling the expression of genes

Motif finding problem is to detect novel, over-represented
unknown signals in a set of sequences (for eg. transcription
factor binding sites in a genome).
Motif Finding Problem
Consensus Pattern - ‘ CCGATTACCGA ’
( l, d ) – (11,2) consensus pattern
Problem Definition
Without any previous knowledge about the consensus
pattern, discover all instances (alignment positions) of the
motifs and then recover the final pattern to which all these
instances are within a given number of mutations.
Complexity of the Problem
Let
n is the length of the DNA sequence
l is the length of the motif
t is the number of sequences
d is the number of mutations in a motif
The running time of a brute force approach:
There are (n-l+1) l-mers in each of t sequences.
Total combination is (n-l+1)t l-mers for t sequences.
Typically, n is much larger than l. ie. n = 600, t = 20.
Existing methodologies
Generative probabilistic representation - continuous
Gibbs Sampling
 Expectation Maximization
 Greedy CONSENSUS
 HMM based

Mismatch representation – Discrete Consensus



Projection Methods
Multiprofiler
Suffix Trees
Existing methodologies
Global Solvers
 Advantage: neighborhood of global optimal solutions.
 Disadvantage: misses out better solutions locally.
 ie: Random Projection, Pattern Branching, etc…
Local Solvers
 Advantage: returns best solution in neighborhood.
 Disadvantage: relies heavily on initial conditions.
 ie: EM, Gibbs Sampling, Greedy CONSENSUS, etc…
Our Approach
Performs global solver to estimate neighborhood of a
promising solution. (Random Projection)
 Using this neighborhood as initial guess, apply local
solver to refine the solution to be the global optimal
solution. (Expectation Maximization)
 Performs efficient neighborhood search to jump out of
convergence region to find another local solutions
systematically.
 A hybrid approach includes the advantages of both the
global and local solvers.

Random Projection
Implements a hash function h(x) to map l-mer onto a kdimensional space.

Hashes all possible l-mers in t sequences into 4k buckets
where each bucket corresponds an unique k-mer.

Imposing certain conditions and setting a reasonable
bucket threshold S, the buckets that exceed S is returned
as the solution.

Expectation Maximization
Expectation Maximization is a local optimal solver in which
we refine the solution yielded by random projection
methodology. The EM method iteratively updates the
solution until it converges to a locally optimal one.
Follow these steps :


Compute the scoring function
Iterate the Expectation step and the Maximization step
Profile Space
A profile is a matrix of probabilities, where the rows represent possible
bases, and the columns represent consecutive sequence positions.
J
k=b
k=1
k=2
k=3
k=4
…
k=l
{A}
C0,1
C1,1
C2,1
C3,1
C4,1
…
Cl,1
{T}
C0,2
C1,2
C2,2
C3,2
C4,2
…
Cl,2
{G}
C0,3
C1,3
C2,3
C3,3
C4,3
…
Cl,3
{C}
C0,4
C1,4
C2,4
C3,4
C4,4
…
Cl,4

Applying the Profile
Space into the coefficient
formula constructs PSSM.
Scoring function-
Maximum Likelihood
Basic Idea
Minimize f ( x)
f : R  R, f  C
N

2
x  f (x)
one-to-one correspondence of the critical points
Local Minimum
Stable Equilibrium Point
Saddle Point
Decomposition Point
Local Maximum
Source
Theoretical Background
Practical Stability Boundary
The problem of finding all the
Tier-1 stable equilibrium points
of xs is the problem of finding
all the decomposition points on
its stability boundary
Theoretical background
Theorem (Unstable manifold of type-1 equilibrium point) :
Let xs1 be a stable e.p. of the gradient system (2) and xd be a type-1
e.p. on the practical stability boundary Ap(xs). Assume that there
exist e and d such that |f (x)| > e unless x  {x : f (x) =0}. If
every e.p. of (1) is hyperbolic and its stable and unstable manifolds
satisfy the transversality condition, then there exists another stable
e.p. xs2 to which the one dimensional unstable manifold of xd
converges.
Our method finds the stability boundary between the two local
minima and traces the stability boundary to find the saddle point.
We used a new trajectory adjustment procedure to move along
the practical stability boundary.
Definitions
Def 1 : x is said to be a critical point of (1) if it satisfies
the condition f (x) = 0 where f (x) is the objective
function assumed to be in C2(n, ).The corresponding
nonlinear dynamical system is
-------- Eq. (1)
The solution curve of Eq. (1) starting from x at time t = 0
is called a trajectory and it is denoted by F( x , .) :  →
n. A state vector x is called an equilibrium point (e.p.)
of Eq. (3) if f ( x ) = 0.
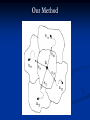
Our Method
Search Directions
Search Directions
Our Method
The exit point method is implemented so that EM can move
out of its convergence region to seek out other local optimal
solutions.






Construct a PSSM from initial alignments.
Calculate eigenvectors of Hessian matrix.
Find exit points (or saddle points) along each eigenvector.
Apply EM from the new stability/convergence region.
Repeat first step.
Return max score {A, a1i, a2j}
Results
Improvements in the Alignment Scores
Motif
Original Pattern
Score
Second Tier Pattern
Score
(11,2)
AACGGTCGCAG
125.1
CCCGGGAGCTG
153.3
(11,2)
ATACCAGTTAC
145.7
ATACCAGGGTC
153.6
(13,3)
CTACGGTCGTCTT
142.6
CCTCGGGTTTGTC
158.7
(13,3)
GACGCTAGGGGGT
158.3
GACCTTGGGTATT
165.8
(15,4)
CCGAAAAGAGTCCGA
147.5
CCGAAAGGACTGCGT
176.2
(15,4)
TGGGTGATGCCTATG
164.6
TGAGAGATGCCTATG
170.4
(17,5)
TTGTAGCAAAGGCTAAA
143.3
CAGTAGCAAAGACTTCC
175.8
(17,5)
ATCGCGAAAGGTTGTGG
174.1
ATTGCGAAAGAATGTGG
178.3
(20,6)
CTGGTGATTGAGATCATCAT
165.9
CATTTAGCTGAGTTCACCTT
194.9
(20,6)
GGTCACTTAGTGGCGCCATG
216.3
CGTCACTTAGTCGCGCCATG
219.7
Improvements in the Alignment Scores
Motif
Original Pattern
Score
Second Tier Pattern
Score
(11,2)
TATCGCTGGGC
147.5
TCTCGCTGGGC
161.1
(13,3)
CACCTTGGTAATT
168.4
GACCATGGGTATT
181.5
(15,4)
ATGGCGTCCGCAATG
174.7
ATGGCGTCCGAAAGA
188.5
(17,5)
CGACACTTTCTCAATGT
178.8
CGACACTATCTTAAGAT
196.2
(20,6)
TCAAATAGACTAGAGGCGAC
189.0
TCTACTAGACTGGAGGCGGC
201.1
Random Projection method results
Performance Coefficient
K is the set of the residue positions of the planted motif
instances, and P is the corresponding set of positions predicted
Results
Alignment Score
200
180
Original
160
Tier-1
Tier-2
140
(2
0,
6)
(1
7,
5)
(1
5,
4)
(1
3,
3)
(1
1,
2)
120
Motifs
Different Motifs and the average score using random starts.
The first tier and second tier improvements on synthetic data.
Results
200
Alignment Score
190
180
Original
170
Tier-1
Tier-2
160
150
(2
0,
6)
(1
7,
5)
(1
5,
4)
(1
3,
3)
(1
1,
2)
140
Motifs
Different Motifs and the average score using random
projection. The first tier and second tier improvements on
synthetic data.
Results
120
Alignment Score
110
100
Original
90
Tier-1
Tier-2
80
70
(2
0,
6)
(1
7,
5)
(1
5,
4)
(1
3,
3)
(1
1,
2)
60
Motifs
Different Motifs and the average score using random projections and the
first tier and second tier improvements on real human sequences.
Results on Real data
Concluding discussion
Using dynamical system approach, we have
shown that the EM algorithm can be improved
significantly.
 In the context of motif finding, we see that
there are many local optimal solutions and it is
important to search the neighborhood space.

Try different global methods and other
techniques like GibbsDNA

Questions and suggestions !!!!!