* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Theoretical Enthalpy
Electrolysis of water wikipedia , lookup
Electrochemistry wikipedia , lookup
Chemical equilibrium wikipedia , lookup
Photoredox catalysis wikipedia , lookup
Bond valence method wikipedia , lookup
Multi-state modeling of biomolecules wikipedia , lookup
Marcus theory wikipedia , lookup
Chemical bond wikipedia , lookup
Asymmetric induction wikipedia , lookup
Process chemistry wikipedia , lookup
Rate equation wikipedia , lookup
Physical organic chemistry wikipedia , lookup
Photosynthetic reaction centre wikipedia , lookup
Hydroformylation wikipedia , lookup
Chemical thermodynamics wikipedia , lookup
Hypervalent molecule wikipedia , lookup
Strychnine total synthesis wikipedia , lookup
Chemical reaction wikipedia , lookup
Transition state theory wikipedia , lookup
George S. Hammond wikipedia , lookup
Hydrogen-bond catalysis wikipedia , lookup
Click chemistry wikipedia , lookup
Lewis acid catalysis wikipedia , lookup
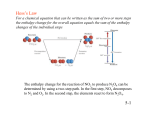
Theoretical Enthalpy: Enthalpy Is a State Function Applications of Hess’s Law Regardless of the pathway the reaction takes, the enthalpy of the reaction will always be the same. Consider: N2(g) + 2O2(g) N2(g) + 2O2(g) → 2NO2(g) ΔH = 68 KJ It is very difficult to run this reaction under normal laboratory conditions. However, the following two reactions are very easy to run in the laboratory: N2(g) + O2(g) → 2NO(g) ΔH = 180 kJ 2NO(g) + O2(g) → 2NO2(g) ΔH = -112 kJ Represented with an energy diagram, it is easy to see how the two reactions can add to give the enthalpy of the net reaction. 2NO(g) 2O2(g) + 2NO(g) ΔH = -112 kJ ΔH = 180 kJ 2NO2(g) ΔH = 68 kJ 2NO2(g) ΔH = 68 KJ Notice what happens when these two reactions are added together: N2(g) + O2(g) → 2NO(g) Δ H = 180 kJ 2NO(g) + O2(g) → 2NO2(g) Δ H = -112 kJ N2(g) + O2(g) + 2NO(g) + O2(g) → 2NO(g) +2NO2(g) Δ H = 68 kJ Simplified: N2(g) + 2O2(g) → 2NO2(g) ΔH = 68 kJ Hess’s Law If a reaction is carried out in a series of steps, ΔH for the reaction will be equal to the sum of the enthalpy changes for the individual steps. N2(g) + 2O2(g) 1 Hess’s Law Hess’s Law H is well known for many reactions, and it is inconvenient to measure H for every reaction in which we are interested. However, we can estimate H using H values that are published and the properties of enthalpy. Using Hess’s Law, we can determine the change of enthalpy of a reaction that can not easily be measured, by measuring simpler stepwise reactions and adding their enthalpies. Example, the conversion of graphite to diamond occurs naturally in the earth’s crust under extreme heat and pressure. Using Hess’s Law find ΔH for: C graphite (s) → C diamond (s) Given: C graphite (s) + O2(g) → CO2(g) ΔH = -394 kJ C diamond (s) + O2(g) → CO2(g) ΔH = -396 kJ Because H is a state function, the total enthalpy change depends only on the initial state of the reactants and the final state of the products. Hess’s Law 1. Using the diagram, write a sequence of thermochemical equations that would net the enthalpy change for the combustion of methane. You must ensure that when you add reactions together, you end up with the correct reactants and the desired product C graphite (s) + O2(g) → CO2(g) ΔH = -394 kJ CO2(g) → C diamond (s) + O2(g) ΔH = -(-396 kJ) C graphite (s) + O2(g) + CO2(g) → C diamond (s) + O2(g) _+ CO2(g) By convention: C graphite (s) → C diamond (s) ΔH = 2 kJ 2 Things to consider when applying Hess’s Law: • If a chemical reaction is reversed, ΔH is also reversed. • The net reaction must contain only the reacting and produced species • The magnitude of ΔH is directly proportional to the quantities described by the coefficients of a balanced chemical reaction. Reactions ΔH (kJ) Example: Diborane(B2H6) is a highly reactive hydride of boron. Calculate ΔH for the synthesis of diborane from its elements, according to the equation: 2B(s) + 3H2(g) → B2H6(g) Given: next slide Practice: Given: (a) 2B(s) + 3/2O2(g) → B2O3(s) -1273 (b) B2H6(g) + 3O2(g) → B2O3(s) + 3H2O(g) -2035 NH3(g) → 1/2N2(g) + 3/2H2(g) ΔH = 46 kJ (c) H2(g) + 1/2 O2(g) → H2O(l) -286 (d) H2O(l) → H2O(g) 2H2(g) + O2(g) → 2H2O(g) 44 ΔH = -484kJ Calculate ΔH for: 2N2(g) + 6H2O(g) → 3O2(g) + 4NH3(g) Then graph using an energy diagram. I find your lack of understanding disturbing A Theoretical Approach We have seen how to determine the enthalpy of a reaction experimentally by calorimetry, and for violent reactions by applying Hess’s Law to a series of reactions carried out separately in a calorimeter. These methods have lead to extensive tables listing the enthalpies of vaporization (∆Hvap), enthalpies of fusion (∆Hfus), enthalpies of reduction (∆Hred), enthalpies of combustion (∆Hcomb), etc… However, a much more useful table can be generated that lists the enthalpies of formation for any pure substance that allows us to calculate the expected enthalpy change when substances undergo chemical reactions. 3 Standard Enthalpy of Formation The change in enthalpy that accompanies the formation of one mole of a compound from its free elements in their standard states. Example: 1/2N2(g) + O2(g) → NO2(g) ΔHof =34 kJ/mol Notice • ΔHof is only for the production of one mole of a substance • ΔHof is zero for any pure element in its standard state 1.Using information from appendix C, write thermochemical equations for both Δ Hof and Δ H for the following compounds: A. Methanol (CH3OH) B. CuO (s) C. Solid rubidium chlorate Standard Enthalpies of Formation Standard enthalpies of formation, Hf, are measured under standard conditions (25°C and 1.00 atm pressure). Determine the ΔH for the previous reaction. N2(g) + 2O2(g) → 2NO2(g) ΔH =68 kJ Remember that ΔHof is for only one mole of a pure substance. The enthalpy change associated with the production of more than one mole is the ΔH of the reaction. 2. Using information from appendix C, write thermochemical equations for ΔHof of the following compounds: A. B. C. D. Methane (CH4) Carbon dioxide Water Oxygen 4 Applying Hess’s Law • The enthalpy change for any reaction is the sum of the enthalpy changes for the formation of each reactant and product. • Examine the following reaction for the combustion of methane C H 4 ( g ) 2 O 2 ( g ) C O 2 ( g ) 2 H 2 O (l ) Hrxn = ? 1. C ( s ) 2 H 2 ( g ) CH 4 ( g ) ΔHof =-75 kJ/mol 2. C ( s ) O2 ( g ) CO2 ( g ) ΔHof =-394 kJ/mol 3. H 2 ( g ) 12 O 2 ( g ) H 2O (l ) ΔHof =-286 kJ/mol CH 4 ( g ) C ( s ) 2 H 2 ( g ) - H1 C ( s ) O2 ( g ) CO2 ( g ) H 2 2 H 2 ( g ) O 2 ( g ) 2 H 2 O (l ) H 3 CH 4 ( g ) 2 O2 ( g ) CO2 ( g ) 2 H 2O (l ) Hrxn ( H 1 ) H 2 2H 3 By multiplying the heat of formation by the number of moles for the balanced reaction, we can determine the enthalpy change for the independent steps, then use Hess’s Law to determine the enthalpy for the net reaction for the combustion of methane. Hrxn = (H2 + 2H3) - H1 Notice, the total enthalpy change is the difference of the product enthalpies minus the reactant enthalpies, each multiplied by the number of moles in the balanced reaction. Hrxn (CH4) = [Hf0(CO2) + 2Hf0(H2O)] - [Hf0(CH4) + 2Hf0(O2) ] 5 Theoretical Calculation of H We can use Hess’s law in this way: 3. 2.Calculate the enthalpy change for the following reactions: H = nHf,products – mHf°,reactants • Nitrogen dioxide gas bubbled through water where n and m are the stoichiometric coefficients. • Combustion of solid glucose (C6H12O6) Thermochemical Stoichiometry Using the change in enthalpy for any chemical reaction, the energy released by, or required by, any reaction given any quantity of reactant or product can be calculated. … you have now been sentenced to die by chemical incineration for being so sweet and chewy little Mr. Gummy Bear. Do you have any last words? 3. Calculate the heats of the reaction for the decomposition of potassium chlorate resulting in the exothermic production of O2 used to execute the “gummy.” ohh No!!! Example: If the metabolism of glucose is the same as the combustion of C6H12O6(s), how much heat is produced by the metabolism of 1.00 g of glucose? 4.How many grams of CH4 are needed to produce enough heat to just boil away 100. mL of water under standard state conditions? 6 Bond Enthalpy and Hess’s Law • Yet another way to estimate H for a reaction is to compare the bond enthalpies of bonds broken to the bond enthalpies of the new bonds formed. Remember the basic premise behind a chemical reaction: Reactant Molecules (bonds broken) atoms Product Molecules (bonds formed) Average Bond Enthalpies • This table lists the average bond enthalpies for many different types of bonds. • Average bond enthalpies are positive, because bond breaking is an endothermic process. Enthalpies of Reaction • • CH4(g) + Cl2(g) CH3Cl(g) + HCl(g) In this example, one C—H bond and one Cl—Cl bond are broken; one C—Cl and one H—Cl bond are formed. Enthalpies of Reaction • Yet another way to estimate H for a reaction is to compare the bond enthalpies of bonds broken to the bond enthalpies of the new bonds formed. • In other words, Hrxn = (bond enthalpies of bonds broken) (bond enthalpies of bonds formed) Average Bond Enthalpies NOTE: These are average bond enthalpies, not absolute bond enthalpies; the C—H bonds in methane, CH4, will be a bit different than the C—H bond in chloroform, CHCl3. Enthalpies of Reaction So, Hrxn = [D(C—H) + D(Cl—Cl) [D(C—Cl) + D(H—Cl) = [(413 kJ) + (242 kJ)] [(328 kJ) + (431 kJ)] = (655 kJ) (759 kJ) = 104 kJ 7 5. Using the bond energies from the “bond reference,” calculate the change in enthalpy for reaction of methane, chlorine and fluorine to produce carbon dichloride diflouride, hydrogen flouride and hydrogen chloride. Also, predict the relative bond lengths of all reactants and products. 8