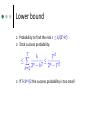Download Lecture 5

Quantum Computing
MAS 725
Hartmut Klauck
NTU
19.3.2012
Simon’s Problem







Given: Black box function f:{0,1}n!{0,1}n
Promise: there is an s2{0,1}n with s0n
 For all x: f(x)=f(x©s)
 For all x,y: x  y©s ) f(x)  f(y)
Find s !
Example: f(x)=2bx/2c
Then for all k: f(2k)=f(2k+1); s=00 ... 01
Simon’s algorithm solve the problem in time/queries poly(n)
Every classical randomized algorithm (even with errors) needs
(2n/2) queries to the black box
The quantum algorithm








Start with|0ni|0ni
Apply Hn to the first n qubits
Apply Uf
Measure qubits n+1,...,2n
Result is some f(z)
There are z, z©s with f(z)=f(z©s)
Remaining state on the first n qubits is
(1/21/2 |zi + 1/21/2|z©si) |f(z)i
Forget |f(z)i
The quantum algorithm






State: 1/21/2 |zi + 1/21/2|z©si
Every z2{0,1}n is equally likely to have been selected
by the measurement (f(z) fixes z and z©s)
We really get a probability distribution on the above
states for a random z
Measuring now would just give us a random z from
{0,1}n [f(z) is chosen randomly in measurement 1,
then with prob. ½ we get: z, with prob. 1/2: z©s,
resulting in a uniformly random z]
How can we get information about s?
Apply Hn
The quantum algorithm




State: 1/21/2 |zi + 1/21/2|z©si
z uniformly random
Apply Hn
Result:
y y |yi with
y=1/21/2 ¢1/2n/2 (-1)y¢z + 1/21/2¢1/2n/2(-1)y¢(z©s)
=1/2(n+1)/2 ¢ (-1)y¢z [1+(-1)y¢s]
y¢z=i yizi
The quantum algorithm







y y |yi with
y=1/2(n+1)/2 ¢ (-1)y¢z [1+(-1)y¢s]
Case 1: y¢s odd ) y=0
Case 2: y¢s even ) y=§ 1/2(n-1)/2
Measure now
[we are now independent of z]
Result: some y:
 yi si ´ 0 mod 2
Hence we get the following equation over Z2
 yi si ´ 0 mod 2
For a random y
Postprocessing





Resulting equation  yi si ´ 0 mod 2
All y with  yi si ´ 0 mod 2 have the same
probability
Knowing this equation reduces the number of
candidates for s by 1/2
We iterate this:
 Repeat n-1 times
 Solve the resulting linear system
If we get n-1 linearly independent equations, then s
is determined
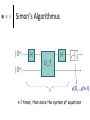
Simon‘s Algorithmus
|0ni
|0ni
H
U_f
H
y(1),...,y(n-1)
n-1 times, then solve the system of equations
Analysis



s is determined as soon as we have n-1 independent
equations. Coefficients of equations are randomly
y(j)1,...,y(j)n under the condition y(j)¢s=0 mod 2
[i.e. from a subspace U of dim. n-1 in (Z2)n]
Probability that y(j+1) is linear independent from y(1),...,y(j):
 Vj=span[y(1),...,y(j)] has dim. j
 Prob, that a random y(j+1) from U is in Vj:
2j/2n-1
Total probability of all being independent:
j=1,...,n-1 (1-2j-1/2n-1)= j=1,...,n-1 (1-1/2j)
Analysis




Total probability of all equations being
independent:
j=1,...,n-1 (1-1/2j)
This is at least
1/2 ¢ (1-[j=2,...,n-1 1/2j])¸ 1/4
[Use (1-a)(1-b)¸ 1-a-b für 0<a,b<1]
I.e. with probability at least 1/4 we find n-1 linear
independent equations, and we can compute s
Use Gaussian elimination O(n3) or other methods
O(n2.373)
Variation


Decision problem:
 With probability 1/2: s=0n
 With prob. 1/2: s uniform from {0,1}n-{0n}
Decide between the two cases
Lower bound






Consider any randomized algorithm that computes s, given
oracle access to f
Fix some f=fs for every s
If there is a randomized algorithm with T queries and success
probability p (both in the worst case), then there is a
deterministic algorithm with T queries and success probability
p for randomly chosen s
Let r2{0,1}m be the string of random bits used
Es Er [Success for fs with random r]=p
) there is a fixed r with
Es [Success fs with r]¸ p
Fix r ) determinististic algorithm
Lower bound









s is uniformly random from {0,1}n-{0n}
Fix any f=fs
Given a deterministic query algorithm, success probability
1/2 for random s
Consider the situation when k queries have been asked
Fixes queries/answers (xi,f(xi))
If there are xi,xj with f(xi)=f(xj), then algo. stops, success
Otherwise: all f(xi) are different,
never xi©xj=s, number of pairs is
Hence there are at least 2n-1- possible s
s is uniformly random from the remaining s
Lower bound





There are still 2n-1- ¸ 2n-k2 posssible s
s uniformly random among those
Query xk+1 (may depend on previous queries and
answers)
For every xk+1 there are k candidates s‘(1),...,s‘(k):
s‘(j)=xj©xk+1 for s
Hence we find the real s with prob. · k/ (2n-k2)
[over choice of s]
Lower bound

Probability to find the real s · k/(2n-k2)
Total success probability:

If T<2n/2/2 the success probability is too small

Variation



Decision problem:
 With probability 1/2: s=0n
 with prob. 1/2: s uniform from {0,1}n-{0n}
Algorithm decides between the two cases
Analysis similar, with less than 2n/2/2 queries error
larger than 1/4
Summary


Simon‘s problem can be solved by a quantum
algorithm with time O(n2.373) and O(n) queries with
success probability 0.99
Every classical randomized algorithm with success
probability 1/2 needs (2n/2) queries
Algorithms so far

Deutsch-Josza and Simon:
 DJ: f balanced or constant
 S: f has „Period“ s (over (Z2)n)
 First Hadamard, then Uf, then Hadamard and
measurement
 D-J: black box with output (-1)f(x)
 S: standard black box
Order finding over ZN






Given numbers x, N, x<N
Order r(x) of x in ZN:
min. r: xr =1 mod N
„Period“ of the powers of x
We will use a black box Ux,N that computes
Ux,N |ji|ki= |ji|xjk mod Ni
x and N have no common divisors
Quantum algorithm to find r(x) ?
Note: we will not really need a black box, since
Ux,N can be computed easily
But first….






We need to say what it means to have an efficient
quantum algorithm
Don’t want to count queries to a black box, but just
computation time (or space)
Efficient classical computation is captured by
complexity classes like P or BPP
P : problems solvable by poly-time Turing machines
BPP : problems solvable by poly-time randomized
Turing machines with bounded error
The classes are believed to be the same
(derandomization)
Computing with circuits








Circuit: inputs x1,…,xn2{0,1}n
Gates g1,…,gm
Gate: takes inputs or output of a previous gate, computes a
function {0,1}2{0,1}
Gates form a directed acyclic graph
Output gate gm
Size: m (corresponds to sequential computation time)
Circuit bases (allowed function for the gates):
 AND, OR, NOT
 NAND
 All Boolean function with 2 inputs
Size changes only by a constant factor with the basis
Probabilistic circuits


Additional inputs r1,…,rm
For all inputs x1,…,xn : if r1,…,rm are uniform random
bits, the correct result will be computed with
probability 2/3
Circuit families






A circuit Cn computes on inputs with n bits
Circuit family (Cn)n2 N
Uniformity condition: Cn can be computed in
polynomial time from n (given in unary)
Without this condition circuit families can compute
everything
Now we can define P, BPP in terms of circuits
 Polynomial size and uniform
Equivalent to Turing machine definitions
Facts about circuits



Almost all function {0,1}n{0,1} need circuit size
(2n/n)
 Established by a counting argument
This bound is tight for non-uniform circuits, i.e.,
every function f:{0,1}n{0,1} can be computed in
size O(2n/n)
We don‘t know any explicit function that needs !(n)
circuit size
Quantum circuits






n qubits initialized with the input (classical state)
s qubits workspace
At all times there is a global state on n+s qubitts
Unitary operations (on 1, 2, or 3 qubits)
U1,…,UT; given together with choice of the qubits
Applying operation Ui : take the tensor product with
the identity on the other qubits, multiply with the
current state in the order: 1,...,T
One or more fixed qubits are measured in the end
(standard basis)
Quantum circuits

Uniform families defined as before, but we need to restrict
the set of allowed unitaries (since the set of all unitaries on a
single qubit is already not even countable)

Class BQP: functions computable by uniform families of
polynomial size quantum circuits with error < 1/3
EQP: same, but no error allowed
It is possible to show that these classes coincide with
definitions for them based on quantum Turing machines


Relationships between
complexity classes

P µ BPP µ BQP µ PSPACE

P µ EQP µ BQP

All inclusions except the first and the last need to be proved
Conclusion: BQP does not contain uncomputable functions
Widely believed that P=BPP
On the other hand the factorization problem is BQP, not known to be
in BPP
Generally considered (very) unlikely BQP=PSPACE, or NPµBQP,
i.e. not likely that we can solve NP -complete problems




Simulating quantum circuits




Theorem:
Every quantum circuit with m gates and n+s can be
simulated by a deterministic circuit of size m¢2O(n+s)
This implies that at most exponential speedups are
possible
Uniformity is preseved by the simulation
Idea: store the global quantum state on n+s qubits
explicitly (with limited precision), apply the m
unitary operations one after another by performing
matrix multiplication (with limited precision)
P vs. BQP


Simulation of classical circuits
Problem:
 Quantum circuits are reversible (up to the final
measurement)
 „Fan-Out“ is not implementable due to nocloning (i.e., using a computation result several
time is not directly possible)
 Solution: Simulate a classical circuit first by a
classical reversible circuit
Simulation






Toffolli Gate:
maps a,b,c to a,b, (aÆb)©c
The Toffolli gate is reversible
[given a,b,d can compute c=(aÆb)©d ]
The gate is universal
[AND: set c=0,
NOT: set c=1, b=1]
Fan-out:
To copy a set b=1, c=0 (copies classical bits)
Classical reversible circuits are also quantum circuits
Simulation of probabilistic circuits is immediate, hence
BPP µ BQP
 Measure 1/21/2 ( |0ki+|1ki ) to get k copies of a random
bit
Which classes of unitaries are
universal?

We can use one of the following
 CNOT and every unitary gate on 1 Qubit
 CNOT, Hadamard, plus O(1) rotation gates (approximately
universal)
 Toffoli Gate and Hadamard gates (approximately
universal)

We can approximate any circuit with 2 qubit gates to any
precision using only gates from one of the above sets with
limited overhead
Approximate computation

What is the influence of error?
Limited precision




Suppose a quantum circuit computes
|Ti=UT UT-1  U1 |xi |0…0i
Ui unitary
Instead of UT apply VT
 errors due to implementation
 while simulating the circuit with limited
precision
Result is VT|T-1i=|Ti+|ETi, where
|ETi=(VT-UT) |T-1i (not normalized)
Limited precision






Result VT|T-1i=|Ti+|ETi, where
|ETi=(VT-UT) |T-1i
Use Vi instead of Ui for all i:
|1i=V1|0i=|1i+|E1i
|2i=V2|1i=|2i+|E2i+V2|E1i
|Ti=VT|T-1i
=|Ti +|ETi +VT|ET-1i + + VTV2 |E1i
Hence k |Ti - |Ti k
· i=1…T k |Eii k =i=1…T k (Vi-Ui) |i-1i k
Approximating unitaries





Let U be an arbitrary unitary on n qubits
And U‘ be any operator
What is the approximation error?
Spectral norm kUk=maxx: kxk=1 k U x k
Approximation error: k U – U‘ k
Total approximation error





i=1…T k (Vi-Ui) |i-1i k · i=1…T k (Vi-Ui) k
If kVi-Uik · /T, then the total distance is at most 
k |Ti - |Ti k ·  implies what error?
Measure all n+s qubits in the standard basis
Measurement result a appears with probability
P(a)=|h a|Ti|2 resp. Q(a)=|h a|Ti|2
Total approximation error



Measurement result a appears with probability
P(a)=|h a|Ti|2 resp. Q(a)=|h a|Ti|2
Hence the total error is at most
a|P(a)-Q(a)|· 2 k |Ti - |Ti k · 2
Conclusion


For polynomial time computations we need to apply
unitaries with precision 1/poly(n) in the spectral
norm
In particular: quantum computing is not an
analogue model of computation requiring infinite
precision
Efficiency of approximating



Number of gates from a finite set we need to
simulate any 1-qubit gate? Depends on the required
precision
[Solovay, Kitaev] show -approximation with
log2(1/) gates
If poly(n) gates have to be approximated with error
1/poly(n) we only need an overhead factor log2(n)