* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download z Tests and Intervals
Survey
Document related concepts
Transcript
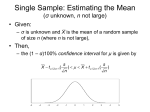
1 Chapter 9.1: z Tests and Confidence Intervals for a Difference Between Two Population Means Instructor: Dr. Arnab Maity 2 In Chapter 8, we learned about the following. • Tests about a mean of a single population – z test (when either σ is known OR sample size n is large) – t test (when either σ is unknown AND sample size n is small) In this chapter, we will learn how to do inference about the difference between means of two populations. Setting: We have two populations with means µ1 and µ2 . We are interested in the difference ∆ = µ1 − µ2 . • Let µ1 denote true average Rockwell hardness for heat-treated steel specimens and µ2 denote true average hardness for cold-rolled specimens. Then an investigator might wish to use samples of hardness observations from each type of steel as a basis for calculating an interval estimate of µ1 − µ2 , the difference between the two true average hardness. • In the above example, another problem of interest is to test whether the Rockwell hardness of the two types of steel is equal. In other words, one may want to test the hypothesis H0 : µ1 − µ2 = 0. Data and point estimators: We observe random samples from each of the two populations. • X1 , · · · , Xm is a random sample with mean µ1 and variance σ12 . • Y1 , · · · , Yn is a random sample with mean µ2 and variance σ22 . • The X and Y samples are independent of each other. • Point estimators: µ̂1 = µ̂2 = ˆ = ∆ Result: Under the above assumptions, we have • E(X̄ − Ȳ ) = µ1 − µ2 . • V ar(X̄ − Ȳ ) = σ12 /m + σ22 /n. These two results are valid without assumptions on the underlying distributions of the two samples. Thus we can obtain an unbiased estimator for the mean difference ∆ = µ1 − µ2 without any distributional assumptions. But in order to construct CI or to develop a test on ∆, we need further assumptions, if the sample size is not large. 3 Case 1: Normal populations with known variances Null hypothesis: H0 : µ1 − µ2 = ∆0 . Test statistic: X̄ − Ȳ − ∆0 Z= q 2 . σ22 σ1 + n m Null distribution: Under H0 , the test statistic has a standard normal [N(0,1)] distribution. Alternative Hypothesis Ha : µ1 − µ2 > ∆0 Ha : µ1 − µ2 < ∆0 Ha : µ1 − µ2 6= ∆0 Rejection Region for Level α Test z ≥ zα (upper-tailed) z ≤ −zα (lower-tailed) z ≤ −zα/2 OR z ≥ zα/2 (two-tailed) The 100(1 − α)% Confidence Interval (CI) for µ1 − µ2 For normal distributions with known σ1 and σ2 : r σ12 σ22 + . (x̄ − ȳ) ± zα/2 m n p-value 1 − Φ(z) Φ(z) 2(1 − Φ(|z|)) 4 1. Does car ownership affect academic achievement? The GPA for m = 100 non-owners of cars had a sample average GPA of 2.70 and a known population variance of 0.36. The n = 100 car owners had a sample average GPA of 2.54 and population variance of 0.40. Do the data present sufficient evidence to indicate a difference in the mean achievement between car owners and non-owners of cars? Use α = 0.05. Solution: (1) Parameter of interest is (2) The null hypothesis is (3) The alternative hypothesis is (4) The test statistic value is 2.7 − 2.54 − 0 x̄ − ȳ − ∆0 q = = 1.84 z= q 2 σ1 σ22 0.36 0.4 + + n 100 100 m (5) The rejection region is (6) Conclusion: Another way to answer the same question is by calculating the p-value. The p-value is: 2(1 − Φ(|z|)) = 2(1 − Φ(1.85)) = 0.064. 5 Case 2: Large sample tests with m > 40 and n > 40 Suppose that the populations may not be normal and the σs are unknown. Then the test statistic: X̄ − Ȳ − ∆0 Z= q 2 , s22 s1 + n m where s21 is the sample variance of X sample, and s22 is the sample variance of Y sample. The rejection region and p-value can be calculated as in the earlier z-tests. The 100(1 − α)% Confidence Interval (CI) for µ1 − µ2 For large sample sizes (with both m and n are large): r s21 s22 x̄ − ȳ ± zα/2 + . m n The upper and lower confidence bounds can be obtained by replacing zα/2 with zα and retaining the appropriate sign (+ or −). 2. A new method of storing snap beans is believed to retain more ascorbic acid than the old method. In an experiment, snap beans were harvested under uniform conditions and frozen in 250 equal-size packages. One hundred of those packages were randomly selected and stored according to the new method, and the other 150 packages were stored by the old method. Subsequently, ascorbic acid determinations (in mg/kg) were made, and the following summary statistics were calculated. New method Sample Size 100 Sample Mean ascorbic acid 450 Sample standard deviation 20 Old Method 150 410 45 (a) Perform the appropriate test at a 1% level of significance. 6 (b) Construct a 95% confidence interval for the difference in the mean amount of ascorbic acid retained. (c) Does the confidence interval suggest that the new method retains more ascorbic acid than the old method? 7 3. Big Foods Grocery has two grocery stores located in Raleigh. One store is located on First Street and the other on Main Street and each is run by a different manager. Each manager claims that her store’s layout maximizes the amounts customers will purchase on impulse. Both managers surveyed a sample of their customers and asked them how much more they spent than they had planned to, in other words, how much did they spend on impulse? For manager 1, 45 subjects were sampled and the sample mean was $3.14 with a standard standard deviation of $1.99. For manager 2, 51 subjects were sampled and the sample mean was $2.64 with a standard standard deviation of $1.29. • Does either manager have a claim as begin different? Conduct a hypothesis test using α = 0.1. • Find a 90% Confidence Interval for the mean difference. Are your conclusions the same as above? Why?