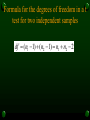* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter 9: Introduction to the t statistic OVERVIEW 1. A sample
Survey
Document related concepts
Transcript
Chapter 10 The t Test for Two Independent Samples PSY295 Spring 2003 Summerfelt Overview Introduce the t test for two independent samples Discuss hypothesis testing procedure Vocabulary lesson New formulas Examples Learning Objectives Know when to use the t test for two independent samples for hypothesis testing with underlying assumptions Compute t for independent samples to test hypotheses about the mean difference between two populations (or between two treatment conditions) Evaluate the magnitude of the difference by calculating effect size with Cohen’s d or r2 Introducing the t test for two independent samples Allows researchers to evaluate the difference between two population means using data from two separate samples Independent samples Between two distinct populations (men vs. women) Between two treatment conditions (distraction v. nondistraction) No knowledge of the parameters of the populations (μ and σ2) Vocabulary lesson Independent Design that uses separate sample for each condition Repeated Design Pooled measures/Between-subjects design measures/Within-subjects design that uses the same sample in each condition variance (weighted mean of two sample variances) Homogeneity of variance assumption Discuss hypothesis testing procedure 1. State hypotheses and select a value for α 2. Locate a critical region (sketch it out) 3. Add the df from each sample and use the t distribution table Compute the test statistic 4. Null hypothesis always state a specific value for μ Same structure as single sample but now we have two of everything Make a decision Reject or “fail to reject” null hypothesis The t Test formula Difference in the means over the standard error One Sample Two Samples X t sX ( X 1 X 2 ) ( 1 2 ) t sX 1 X 2 Formula for the degrees of freedom in a t test for two independent samples df (n1 1) (n2 1) n1 n2 2 Estimating Population Variance Need variance estimate to calculate the standard error Since these variances are unknown, we must estimate them Pooling the sample variances proves to be the best way Add the sums of squares for each sample and divide by the sum of the df of each sample SS1 SS 2 s df1 df 2 2 p Calculating the Standard Error for the t statistic Using the pooled variance estimate in the original formula for standard error old s X s2 n new sx1 x 2 s 2p n1 s 2p n2 Magnitude of difference by computing effect size Two methods for computing effect size Cohen’s d d X1 X 2 s r2 2 t r2 2 t df 2 p Example Researcher wants to assess the difference in memory ability between alcoholics and nondrinkers Sample of n=10 alcoholics, sample of n=10 nondrinkers Each person given a memory test that provides a score Alcoholics; mean=43, SS=400 Non-Drinkers; mean=57, SS=410 Example, continued What if the introduction read… A researcher wants to assess the damage to memory that is caused by chronic alcoholism Would that change the analysis?