* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture11
History of electric power transmission wikipedia , lookup
Ground (electricity) wikipedia , lookup
Topology (electrical circuits) wikipedia , lookup
Mechanical-electrical analogies wikipedia , lookup
Flexible electronics wikipedia , lookup
Ground loop (electricity) wikipedia , lookup
Signal-flow graph wikipedia , lookup
Power inverter wikipedia , lookup
Immunity-aware programming wikipedia , lookup
Three-phase electric power wikipedia , lookup
Electrical ballast wikipedia , lookup
Electrical substation wikipedia , lookup
Schmitt trigger wikipedia , lookup
Voltage regulator wikipedia , lookup
Nominal impedance wikipedia , lookup
Power electronics wikipedia , lookup
Voltage optimisation wikipedia , lookup
Power MOSFET wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Two-port network wikipedia , lookup
Stray voltage wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Surge protector wikipedia , lookup
Buck converter wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Zobel network wikipedia , lookup
Current source wikipedia , lookup
Alternating current wikipedia , lookup
Mains electricity wikipedia , lookup
Opto-isolator wikipedia , lookup
AC STEADY-STATE ANALYSIS
SINUSOIDAL AND COMPLEX FORCING FUNCTIONS
Behavior of circuits with sinusoidal independent sources
and modeling of sinusoids in terms of complex exponentials
PHASORS
Representation of complex exponentials as vectors. It facilitates
steady-state analysis of circuits.
IMPEDANCE AND ADMITANCE
Generalization of the familiar concepts of resistance and
conductance to describe AC steady state circuit operation
PHASOR DIAGRAMS
Representation of AC voltages and currents as complex vectors
BASIC AC ANALYSIS USING KIRCHHOFF LAWS
ANALYSIS TECHNIQUES
Extension of node, loop, Thevenin and other techniques
SINUSOIDAL AND COMPLEX FORCING FUNCTIONS
KVL : L
di
(t ) Ri (t ) v (t )
dt
In steady state i (t ) A cos( t ), or
i (t ) A1 cos t A2 sin t
*/ R
If the independent sources are sinusoids di
*/ L
(t ) A1 sin t A2 cos t
of the same frequency then for any
dt
variable in the linear circuit the steady
state response will be sinusoidal and of ( LA1 RA2 ) sin t ( LA2 RA1 ) cos t
the same frequency
VM cos t
LA1 RA2 0 algebraic problem
LA2 RA1 VM
To determine the steady state solution
we only need to determine the parameters A1 RVM , A2 LVM
2
2
2
2
R
(
L
)
R
(
L
)
B,
v (t ) Asin( t ) iSS (t ) B sin( t )
Determining the steady state solution can
be accomplished with only algebraic tools!
FURTHER ANALYSIS OF THE SOLUTION
The solution is i (t ) A1 cos t A2 sin t
The applied voltage is v (t ) VM cos t
For comparison purposes one can write i (t ) A cos( t )
A1 A cos , A2 Asin
A1
A A12 A22 , tan
RVM
LVM
,
A
2
R 2 (L) 2
R 2 (L) 2
A
i (t )
VM
R 2 (L) 2
, tan 1
VM
R (L)
2
2
A2
A1
L
R
cos( t tan 1
L
R
)
For L 0 the current ALWAYS lags the voltage
If R 0 (pure inductor) the current lags the voltage by 90
SOLVING A SIMPLE ONE LOOP CIRCUIT CAN BE VERY LABORIOUS
IF ONE USES SINUSOIDAL EXCITATIONS
TO MAKE ANALYSIS SIMPLER ONE RELATES SINUSOIDAL SIGNALS
TO COMPLEX NUMBERS. THE ANALYSIS OF STEADY STATE WILL BE
CONVERTED TO SOLVING SYSTEMS OF ALGEBRAIC EQUATIONS ...
… WITH COMPLEX VARIABLES
ESSENTIAL IDENTITY : e j cos j sin (Euler identity)
v (t ) VM cos t y (t ) A cos( t )
v (t ) VM sin t y (t ) A sin( t ) * / j (and add)
VM e j t Ae j (t ) Ae j e j t
y(t )
If everybody knows the frequency of the sinusoid
then one can skip the term exp(jwt)
VM Ae j
Example
R jL R2 (L )2 e
I M e j
v (t ) VM e j t
Assume i (t ) I M e ( j t )
di
KVL : L (t ) Ri (t ) v (t )
dt
di
(t ) jI M e ( j t )
dt
di
L (t ) Ri (t ) jLI M e ( j t ) RI M e ( j t )
dt
( jL R) I M e ( j t )
j
( jL R) I M e e
jt
( jL R) I M e j e j t VM e j t
VM
R jL
I M e j
*/
jL R
R jL
I M e j
VM ( R jL)
R 2 (L) 2
IM
VM
R 2 (L ) 2
VM
R 2 (L ) 2
tan 1
e
L
R
tan 1
L
R
, tan 1
L
R
v (t ) VM cos t Re{VM e j t }
i (t ) Re{I M e ( j t ) } I M cos( t )
C P
x jy re j
r x 2 y 2 , tan 1
x r cos , y r sin
y
x
PHASORS
ESSENTIAL CONDITION
ALL INDEPENDENT SOURCES ARE SINUSOIDS OF THE SAME FREQUENCY
BECAUSE OF SOURCE SUPERPOSITION ONE CAN CONSIDER A SINGLE SOURCE
u(t ) U M cos( t )
THE STEADY STATE RESPONSE OF ANY CIRCUIT VARIABLE WILL BE OF THE FORM
y(t ) YM cos( t )
SHORTCUT 1
u(t ) U M e j ( t ) y(t ) YM e
Re{U M e j ( t ) } Re{YM e
j ( t )
j ( t )
}
U M e j ( t ) U M e j e jt u U M e j y YM e j
SHORTCUT IN NOTATION
NEW IDEA:
INSTEAD OF WRITING u U M e j WE WRITE u U M
... AND WE ACCEPT ANGLES IN DEGREES
U M IS THE PHASOR REPRESENTA TION FOR U M cos( t )
u(t ) U M cos( t ) U U M Y YM y(t ) YM cos( t )
SHORTCUT 2: DEVELOP EFFICIENT TOOLS TO DETERMINE THE PHASOR OF
THE RESPONSE GIVEN THE INPUT PHASOR(S)
Example
It is essential to be able to move from
sinusoids to phasor representation
A cos(t ) A
A sin(t ) A 90
V V M 0
v Ve jt
I I M
jt
di
i
Ie
L (t ) Ri (t ) v
dt
L( jIe jt ) RIe jt Ve jt
In terms of phasors one has
jLI RI V
V
I
R jL
The phasor can be obtained using
only complex algebra
We will develop a phasor representation
for the circuit that will eliminate the need
of writing the differential equation
v (t ) 12 cos(377t 425) 12 425
y(t ) 18 sin( 2513t 4.2) 18 85.8
Given f 400 Hz
V1 1020 v1 (t ) 10 cos(800 t 20)
V2 12 60 v2 (t ) 12 cos(800 t 60)
Phasors can be combined using the
rules of complex algebra
(V11)(V2 2 ) V1V2(1 2 )
V11 V1
(1 2 )
V2 2 V2
PHASOR RELATIONSHIPS FOR CIRCUIT ELEMENTS
RESISTORS v (t ) Ri (t )
VM e ( j t ) RI M e ( j t )
VM e j RI M e j
V RI Phasor representation for a resistor
Phasors are complex numbers. The resistor
model has a geometric interpretation
The voltage and current
phasors are colineal
In terms of the sinusoidal signals this
geometric representation implies that
the two sinusoids are “in phase”
INDUCTORS
d
( I M e ( j t ) )
dt
jLI M e ( j t )
VM e ( j t ) L
Relationship between sinusoids
VM e j jLI M e j
V jLI
Example
The relationship between L 20mH , v (t ) 12 cos(377t 20). Find i (t )
phasors is algebraic
For the geometric view
use the result
j 190 e j 90
V LI90
377
1220
( A)
V 1220 I
L90
V
12
I
I
70( A)
jL
377 20 103
i (t )
The voltage leads the current by 90 deg
The current lags the voltage by 90 deg
12
cos(377t 70)
3
377 20 10
CAPACITORS
I M e ( j t ) C
d
(VM e ( j t ) )
dt
Relationship between sinusoids
I M e j jCe j
I CV90
I jCV
C 100 F , v (t ) 100 cos(314t 15). Find i (t )
The relationship between
phasors is algebraic
In a capacitor the
current leads the
voltage by 90 deg
The voltage lags
the current by 90 deg
314
V 10015
I jCV
I C 190 10015
I 314 100 106 100105( A)
i (t ) 3.14 cos(314t 105)( A)
L 0.05 H , I 4 30( A), f 60 Hz
Find the voltage across the inductor
2 f 120
V jLI
V 120 0.05 190 4 30
V 2460
v (t ) 24 cos(120 60)
Now an example with capacitors
C 150 F , I 3.6 145, f 60 Hz
Find the voltage across the capacitor
2 f 120
I jCV V
V
I
jC
3.6 145
120 150 106 190
200
V
235
v (t )
200
cos(120 t 235)
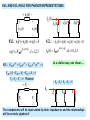
IMPEDANCE AND ADMITTANCE
For each of the passive components the relationship between the voltage phasor
and the current phasor is algebraic. We now generalize for an arbitrary 2-terminal
element
Z ( ) R( ) jX ( )
R( ) Resistive component
X ( ) Reactive component
| Z | R 2 X 2
X
z tan 1
R
(INPUT) IMPEDANCE
V V V
Z M v M ( v i ) | Z | z
I I M i I M
(DRIVING POINT IMPEDANCE)
The units of impedance are OHMS
Impedance is NOT a phasor but a complex
number that can be written in polar or
Cartesian form. In general its value depends
on the frequency
Element Phasor Eq. Impedance
R
L
C
V RI
V jLI
1
V
I
jC
ZR
Z j L
1
Z
j C
KVL AND KCL HOLD FOR PHASOR REPRESENTATIONS
v2 (t )
v1 ( t )
v3 ( t )
i0 (t )
i1 (t )
i2 ( t )
i3 (t )
KVL: v1(t ) v2 (t ) v3 (t ) 0
KCL : i0 (t ) i1 (t ) i2 (t ) i3 (t ) 0
vi (t ) VMie j ( t i ) , i 1,2,3
ik (t ) I Mk e j ( t k ) , k 0,1,2,3
In a similar way, one shows ...
KVL : (VM 1e j1 VM 2e j 2 VM 3e j 3 )e jt 0
VM11 VM 2 2 VM 33 0
V1 V2 V3 0 Phasors!
V2
V1
V3
I0 I1 I 2 I3 0
I0
I1
I2
I3
The components will be represented by their impedances and the relationships
will be entirely algebraic!!
SPECIAL APPLICATION:
IMPEDANCES CAN BE COMBINED USING THE SAME RULES DEVELOPED
FOR RESISTORS
I
V1
Z1
I
V2
I
Zs Z1 Z2
Z2
Z1
Z2 V
V
1
1
k
Zp
Zk
Z s k Zk
LEARNING EXAMPLE
I
Zp
Z1Z 2
Z1 Z 2
f 60 Hz, v (t ) 50 cos( t 30)
Compute equivalent impedance and current
120 , V 5030, Z R 25
ZR R
Z L jL
ZC
1
jC
1
j120 50 106
Z L j 7.54, ZC j53.05
Z L j120 20 103 , ZC
Z s Z R Z L ZC 25 j 45.51
I
V
5030
5030
( A)
( A)
Z s 25 j 45.51
51.93 61.22
I 0.9691.22( A) i (t ) 0.96 cos(120 t 91.22)( A)
Parallel Combinatio n of Admittances
(COMPLEX) ADMITTANCE
Y p Yk
1
G jB (Siemens)
Z
G conductanc e
B Suceptanc e
Y
k
YR 0.1S
1
1
R jX
R jX
2
Z R jX
R jX R X 2
R
R2 X 2
X
B 2
R X2
G
L
C
V RI
V jLI
1
V
I
jC
ZR
Z jL
Z
1
jC
1
j1( S )
j1
Y p 0.1 j1( S )
Series Combinatio n of Admittanc es
1
1
Ys k Yk
0.1S
Element Phasor Eq. Impedance
R
YC
Admittance
1
Y G
R
1
Y
j L
Y j C
j 0.1S
1
1
1
Ys 0.1 j 0.1
10 j10
(0.1)( j 0.1) 0.1 j 0.1
0.1 j 0.1 0.1 j 0.1
1
10 j10
Ys
10 j10
200
Ys 0.05 j 0.05 S
Ys
FIND THE IMPEDANCE ZT
Z1 4 j 6 j 4
Z1 4 j 2
Y12 Y1 Y2
( R P ) Z1 4.47226.565
Y1 0.224 26.565
( P R)Y1 0.200 j 0.100
Y12 Y1 Y2 0.45 j 0.35
( R P )Y12 0.570 37.875
Z12 1.75437.875
( P R) Z12 1.384 j1.077
Z2 2 j 2 ( R P ) Z2 2.82845
Y2 0.354 45
( P R)Y2 0.250 j 0.250
1
4 j2
ZT 2 (1.384 j1077) 3.383 j1.077
Y1
2
4 j 2 (4) (2) 2
1
2 j2
Y2
2
2 j 2 (2) (2) 2
1
1
0.45 j 0.35
Z12
Y12 0.45 j 0.35
0.325
1
Z12
Y12
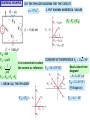
PHASOR DIAGRAMS
Display all relevant phasors on a common reference frame
Very useful to visualize phase relationships among variables.
Especially if some variable, like the frequency, can change
SKETCH THE PHASOR DIAGRAM FOR THE CIRCUIT
Any one variable can be chosen as reference.
For this case select the voltage V
KCL : I S
V
V
jCV
R jL
(capacitiv e)
| I L || IC |
| I L || IC |
IC jCV
IL
V
jl
INDUCTIVE CASE
CAPACITIVE CASE
(inductive )
LEARNING EXAMPLE
DO THE PHASOR DIAGRAM FOR THE CIRCUIT
377( s 1 )
2. PUT KNOWN NUMERICAL VALUES
| VL VC || VR |
VR RI
VL jLI
It is convenient to select
1
the current as reference
VC
I
j C
VS VR VL VC
1. DRAW ALL THE PHASORS
| VL || VC |
DIAGRAM WITH REFERENCE VS 12 290
VL 18135(V )
Read values from
diagram!
I 345( A)
VR 1245(V )
(Pythagoras)
VC 6 45
BASIC ANALYSIS USING KIRCHHOFF’S LAWS
PROBLEM SOLVING STRATEGY
For relatively simple circuits use
Ohm' s law for AC analysis; i.e., V IZ
The rules for combining Z and Y
KCL AND KVL
Current and voltage divider
For more complex circuits use
Node analysis
Loop analysis
Superposit ion
Thevenin' s and Norton' s theorems
MATLAB
PSPICE
ANALYSIS TECHNIQUES
PURPOSE: TO REVIEW ALL CIRCUIT ANALYSIS TOOLS DEVELOPED FOR
RESISTIVE CIRCUITS; I.E., NODE AND LOOP ANALYSIS, SOURCE SUPERPOSITION,
SOURCE TRANSFORMATION, THEVENIN’S AND NORTON’S THEOREMS.
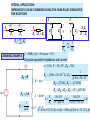
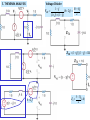
COMPUTE I0
V2 60
V
20 V2 2 0
1 j1
1 j1
1
1
6
V2
1
2
1 j1
1 j1
1 j1
V2
1. NODE ANALYSIS
V1
V
V
20 2 2 0
1 j1
1 1 j1
V1 V2 60
I0
V2
( A)
1
(1 j1) (1 j1)(1 j1) (1 j1) 2(1 j1) 6
(1 j1)(1 j1)
1 j1
V2
4
8 j2
1 j
V2
(4 j )(1 j )
2
3
5
I 0 j ( A)
2
2
I0 2.92 30.96
Circuit with voltage source
set to zero (SHORT CIRCUITED)
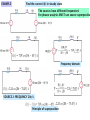
SOURCE SUPERPOSITION
I
I L2
1
L
=
V
1
L
+
Circuit with current
source set to zero(OPEN)
Due to the linearity of the models we must have
I L I L1 I L2
VL VL1 VL2
Principle of Source Superposition
The approach will be useful if solving the two circuits is simpler, or more convenient, than
solving a circuit with two sources
We can have any combination of sources. And we can partition any way we find convenient
VL2
3. SOURCE SUPERPOSITION
I 0' 10( A)
Z ' (1 j ) || (1 j )
(1 j )(1 j )
1
(1 j ) (1 j )
COULD USE SOURCE TRANSFORMATION
TO COMPUTE I"0
V1"
1 j
1 j
I 0"
6
2
j
(
1
j
)
3
j
I 0"
6 ( A)
1 j
6 6
"
1 j
I
j ( A)
0
2 j
4 4
5 3
I 0 I 0' I 0" j ( A)
2 2
Z"
Z " 1 || (1 j )
Z"
Z"
"
"
60(V ) I 0 "
60( A)
Z 1 j
Z 1 j
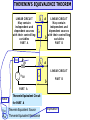
THEVENIN’S EQUIVALENCE THEOREM
LINEAR CIRCUIT
May contain
independent and
dependent sources
with their controlling
variables
PART A
ZTH
RTH
vTH
i
a
vO
b
_
i
a
LINEAR CIRCUIT
vO
_
LINEAR CIRCUIT
May contain
independent and
dependent sources
with their controlling
variables
PART B
b
PART B
PART A
Phasor
Thevenin Equivalent Circuit
for PART A
vTH
Thevenin Equivalent Source
RTH
Thevenin Equivalent Resistance
Impedance
5. THEVENIN ANALYSIS
Voltage Divider
VOC
10 6 j
1 j
(8 2 j )
2
(1 j ) (1 j )
ZTH (1 j ) || (1 j ) 1
8 2j
I0
53j
( A)
2
EXAMPLE
Find the current i(t) in steady state
The sources have different frequencies!
For phasor analysis MUST use source superpositio
Frequency domain
SOURCE 2: FREQUENCY 20r/s
Principle of superposition
LEARNING BY DESIGN
USING PASSIVE COMPONENTS TO CREATE GAINS LARGER THAN ONE
PRODUCE A GAIN=10
AT 1KhZ WHEN R=100
2 LC 1
L 1.59mH
C 15.9 F