Download Chapter 3 Kinetics of Particles

Chapter 3
Kinetics of Particles
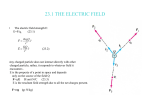
Question 3–1
A particle of mass m moves in the vertical plane along a track in the form of a
circle as shown in Fig. P3-1. The equation for the track is
r = r0 cos θ
Knowing that gravity acts downward and assuming the initial conditions θ(t =
0) = 0 and θ̇(t = 0) = θ̇0 , determine (a) the differential equation of motion for
the particle and (b) the force exerted by the track on the particle as a function
of θ.
r=
O
r0
θ
os
c
θ
Figure P 3-1
m
g
62
Chapter 3. Kinetics of Particles
Solution to Question 3–1
Kinematics
Let F be a reference frame fixed to the track. Then, choose the following coordinate system fixed in reference frame F :
Ex
Ez
Ey
Origin at point O
=
=
=
Along OP when θ = 0
Out of page
Ez × Ex
Next, let A be a reference frame fixed to the direction OP . Then, choose the
following coordinate system fixed in reference frame A:
er
ez
eθ
Origin at point O
=
=
=
Along OP
Ez
ez × er
The geometry of the bases {Ex , Ey , Ez } and {er , eθ , ez } is shown in Fig. 3-1. Using
Fig. 3-1, we have that
Ex
Ey
= cos θ er − sin θ eθ
(3.1)
= sin θ er + cos θ eθ
(3.2)
Ey
er
eθ
θ
θ
Ex
Figure 3-1
Geometry of Coordinate System for Question 3.1
Next, the position of the particle is given in terms of the basis {er , eθ , ez } as
r = r er = r0 cos θ er
(3.3)
Furthermore, since the angle θ is measured from the fixed horizontal direction,
the angular velocity of A in F is given as
F
ωA = θ̇ez
(3.4)
63
Applying the transport theorem to r from reference frame A to F , the velocity
of the particle in reference frame F as
F
v=
F
dr Adr F A
=
+ ω ×r
dt
dt
(3.5)
Now we have
A
dr
= −r0 θ̇ sin θ er
dt
F A
ω × r = θ̇Ez × r0 cos θ er = r0 θ̇ cos θ eθ
(3.6)
(3.7)
Adding the expressions in Eq. (3.6) and Eq. (3.7), we obtain the velocity in reference frame F as
F
v = −r0 θ̇ sin θ er + r0 θ̇ cos θ eθ
(3.8)
Re-writing Eq. (3.8), we obtain
F
v = r0 θ̇(− sin θ er + cos θ eθ )
(3.9)
The speed in reference frame F is then given as
F
v = kF vk = r0 θ̇
(3.10)
Dividing F v by F v, we obtain the tangent vector as
et = − sin θ er + cos θ eθ
(3.11)
Next, the principal unit normal vector is computed as
en =
F
det /dt
F
k det /dtk
(3.12)
Applying the transport theorem to et , we have
F
A
det
det F A
=
+ ω × et
dt
dt
(3.13)
Now
A
det
dt
F A
ω × et
= −θ̇ cos θ er − θ̇ sin θ eθ
= θ̇ez × (− sin θ er + cos θ eθ )
(3.14)
= −θ̇ cos θ er − θ̇ sin θ eθ
(3.15)
det
= −2θ̇ cos θ er − 2θ̇ sin θ eθ
dt
(3.16)
Consequently,
F
64
Chapter 3. Kinetics of Particles
which implies that
−2θ̇ cos θ er − 2θ̇ sin θ eθ
en =
k − 2θ̇ cos θ er − 2θ̇ sin θ eθ k
= − cos θ er − sin θ eθ
(3.17)
The principal unit bi-normal vector to the track is then obtained as
eb = et × en = (− sin θ er + cos θ eθ ) × (− cos θ er − sin θ eθ ) = ez
(3.18)
The acceleration as viewed by an observer fixed to the track is then obtained as
F
a=
F
d F A d F F A F
v =
v + ω × v
dt
dt
(3.19)
Now we have
A
det
d F v
= r0 θ̈et + r0 θ̇
dt
dt
= r0 θ̈et + r0 θ̇(−θ̇ cos θ er − θ̇ sin θ eθ )
A
= r0 θ̈et + r0 θ̇ 2 (− cos θ er − sin θ eθ )
F
A
ω
F
= r0 θ̈et + r0 θ̇ 2 en
(3.20)
= θ̇eb × r0 θ̇et = r0 θ̇ 2 en
(3.21)
× v = θ̇ez × r0 θ̇et
where we note that the results of Eqs. (3.14) and (3.17) have been used to obtain
the result given in Eq. (3.20). Therefore,
F
a = r0 θ̈et + 2r0 θ̇ 2 en
(3.22)
Kinetics
Next, in order to obtain the differential equation of motion, we need to apply
Newton’s 2nd Law to the particle. The free body diagram of the particle is given
in Fig. 3-2 as where
m
N
mg
Figure 3-2
Free Body Diagram for Question 3–1.
N
= Reaction Force of Track on Particle
mg = Force of Gravity
65
Now we know that the reaction force is orthogonal to the track while gravity
acts vertically downward. Consequently, we have that
N = Nn en + Nb
mg = −mgEy
(3.23)
(3.24)
Then, using the expression for Ey from Eq. (3.2), we obtain the force of gravity
as
mg = −mg(sin θ er + cos θ eθ ) = −mg sin θ er − mg cos θ eθ
(3.25)
The total force on the particle is then given as
F = N + mg = Nn en + Nb eb − mg sin θ er − mg cos θ eθ
(3.26)
Applying Newton’s 2nd Law using the acceleration from Eq. (3.22), we obtain
Nn en + Nb eb − mg sin θ er − mg cos θ eθ = mr0 θ̈et + 2mr0 θ̇ 2 en
(3.27)
Now it is seen that the unknown reaction forces exerted by the track lie in the
directions of en and eb . Therefore, the reaction force exerted by the track can
be eliminated if the scalar product with et is taken with both sides of Eq. (3.27)
as
(Nn en +Nb eb −mg sin θ er −mg cos θ eθ )·et = (mr0 θ̈et +2mr0 θ̇ 2 en )·et (3.28)
Then, observing that en · et = eb · et = 0, Eq. (3.28) simplifies to
−mg sin θ er · et − mg cos θ eθ · et = mr0 θ̈
(3.29)
Now, using the expression for et from Eq. (3.11), we have that
er · et
eθ · et
= er · (− sin θ er + cos θ eθ ) = − sin θ
= eθ · (− sin θ er + cos θ eθ ) = cos θ
(3.30)
(3.31)
Substituting the results of Eq. (3.30) and Eq. (3.31) into Eq. (3.29), we obtain
mg sin2 θ − mg cos2 θ = mr0 θ̈
(3.32)
cos2 θ − sin2 θ = cos 2θ
(3.33)
Now we also note that
Therefore, Eq. (3.32) can be written as
−mg cos 2θ = mr0 θ̈
(3.34)
Next, taking the scalar product of Eq. (3.28) in the en direction, we obtain
Nn − mg sin θ er · en − mg cos θ eθ · en = 2mr0 θ̇ 2
(3.35)
66
Chapter 3. Kinetics of Particles
Then, using the expression for en from Eq. (3.17), we have that
er · en
eθ · en
= er · (− cos θ er − sin θ eθ ) = − cos θ
= eθ · (− cos θ er − sin θ eθ ) = − sin θ
(3.36)
(3.37)
Substituting the results of Eq. (3.36) and Eq. (3.37) into Eq. (3.35) gives
Nn + mg sin θ cos θ + mg cos θ sin θ = 2mr0 θ̇ 2
(3.38)
Now we have that
sin θ cos θ + cos θ sin θ = 2 sin θ cos θ = sin 2θ
(3.39)
Consequently, Eq. (3.38 can be written as
N + mg sin 2θ = 2mr0 θ̇ 2
(3.40)
Finally, taking the scalar product of Eq. (3.28) in the eb direction, we obtain
Nb = 0
(3.41)
The following three scalar equations then result from Eqs. (3.34), Eq. (3.40), and
Eq. (3.41):
mr0 θ̈
2mr0 θ̇
2
= −mg cos 2θ
= Nn + mg sin 2θ
0 = Nb
(3.42)
(3.43)
(3.44)
Since Eq. (3.43) contains no reaction forces, it is the differential equation of
motion, i.e. the differential equation of motion is given as
mr0 θ̈ = −mg cos 2θ
(3.45)
Rearranging this last equation, we obtain the differential equation of motion for
the particle as
g
cos 2θ = 0
(3.46)
θ̈ +
r0
Force Exerted by Track on Particle As a Function of θ
First we note the following:
θ̈ =
dθ̇ dθ
dθ̇
dθ̇
=
= θ̇
dt
dθ dt
dθ
(3.47)
Substituting Eq. (3.47) into Eq. (3.46), we obtain
θ̇
dθ̇
g
+
cos 2θ = 0
dθ
r0
(3.48)
67
Rearranging Eq. (3.48) and separating variables, we obtain
θ̇dθ̇ = −
g
cos 2θdθ
r0
(3.49)
Integrating this last equation, we obtain
g
1 2
θ̇ − θ̇02 = −
[sin 2θ]θθ0
2
2r0
(3.50)
Noting that θ(t = 0) = 0, this last equation simplifies to
θ̇ 2 = θ̇02 −
g
sin 2θ
r0
(3.51)
Solving for the reaction force using Eq. (3.42), we obtain
We then obtain
Nn = 2mr0 θ̇ 2 − mg sin 2θ
(3.52)
g
Nn = 2mr0 θ̇02 −
sin 2θ − mg sin 2θ
r0
(3.53)
Simplifying this last equation, we obtain
Nn = 2mr0 θ̇02 − 3mg sin 2θ
The force exerted by the track on the particle is then given as
h
i
N = 2mr0 θ̇02 − 3mg sin 2θ en
(3.54)
(3.55)
68
Chapter 3. Kinetics of Particles
Question 3–2
A collar of mass m slides without friction along a rigid massless rod as shown
in Fig. P3-2. The collar is attached to a linear spring with spring constant K and
unstretched length L. Assuming no gravity, determine the differential equation
of motion for the collar.
O
K
L
m
x
Figure P 3-2
Solution to Question 3–2
First, let F be a fixed reference frame. Then, choose the following coordinate
system fixed in reference frame F :
Ey
Ez
Ex
Origin at Attachment
Point of Spring
=
Up
=
Out of Page
=
Ey × Ez
Then, in terms of the basis {Ex , Ey , Ez }, the position of the collar is given as
r = xEx − LEy
(3.56)
Since reference frame F is fixed and L is constant, the velocity of the collar in
reference frame F is given as
F
v=
F
dr
= ẋEx
dt
(3.57)
Furthermore, the acceleration of the collar in reference frame F is given as
F
a=
F
d F v = ẍEx
dt
(3.58)
Next, using the free body diagram of the collar as shown in Fig. 3-3, we have
that
Fs = Spring Force
N = Reaction Force of Rod on Collar
69
N
Fs
Figure 3-3
Free Body Diagram for Question 3.2
Since the reaction force acts in the Ey direction, we have that
N = NEy
(3.59)
Next, the force in a linear spring is given as
Fs = −K(ℓ − ℓ0 )us
(3.60)
First, the stretched length of the spring is
ℓ = kr − rA k
(3.61)
where the position of the attachment point is zero, i.e., rA = 0. Therefore, the
stretched length of the spring is given as
p
ℓ = krk = kxEx − LEy k = x 2 + L2
(3.62)
Furthermore, the unstretched length of the spring is given as
ℓ0 = L
(3.63)
Finally, the direction from the attachment point to the particle, us , is given as
us =
xEx − LEy
r − rA
= √
kr − rA k
x 2 + L2
(3.64)
Consequently, the force of the spring is given as
Fs = −K
i xEx − LEy
hp
x 2 + L2 − L √
x 2 + L2
(3.65)
Grouping this last expression into components, we obtain
Fs = −K
hp
hp
i
i
x
L
Ex + K x 2 + L2 − L √
Ey
x 2 + L2 − L √
2
2
2
x +L
x + L2
(3.66)
The resultant force acting on the particle is then given as
hp
i
i
hp
x
L
Fs = −K x 2 + L2 − L √
Ex + N + K x 2 + L2 − L √
Ey
x 2 + L2
x 2 + L2
(3.67)
70
Chapter 3. Kinetics of Particles
Applying Newton’s 2nd Law, we obtain
hp
i
i
hp
x
L
2
2
2
2
Ey = mẍEx
Ex + N + K x + L − L √
−K x + L − L √
x 2 + L2
x 2 + L2
(3.68)
Using the Ex -component of the last equation, we obtain
mẍ = −K
hp
i
x 2 + L2 − L √
x
x 2 + L2
(3.69)
Rearranging this last equation, we obtain the differential equation of motion as
mẍ + K
i
hp
x 2 + L2 − L √
x
x2
+ L2
=0
(3.70)
71
Solution to Question 3–3
A bead of mass m slides along a fixed circular helix of radius R and constant
helical inclination angle φ as shown in Fig. P3-3. The equation for the helix is
given in cylindrical coordinates as
z = Rθ tan φ
(3.71)
Knowing that gravity acts vertically downward, determine the differential equation of motion for the bead in terms of the angle θ using (a) Newton’s 2nd law
and (b) the work-energy theorem for a particle. In addition assuming the initial
conditions θ(t = 0) = θ0 and θ̇(t = 0) = θ̇0 , determine (c) the displacement
attained by the bead when it reaches its maximum height on the helix.
g
R
A
Om P
θ
φ
z
Figure P 3-3
Solution to Question 3–3
Kinematics
Let F be a reference frame fixed to the helix. Then, choose the following coordinate system fixed in reference frame F :
Ex
Ey
Ez
Origin at O
=
=
=
Along er at t = 0
Along eθ at t = 0
er × eθ
Next, let A be a reference
n frameo that rotates with the projection of the position of particle into the Ex , Ey -plane. Corresponding to A, we choose the
72
Chapter 3. Kinetics of Particles
following coordinate system to describe the motion of the particle:
er
ez
eθ
Origin at O
=
=
=
Along Radial Direction of Circle
Ez from Reference Frame F
ez × er
Now, since φ is the angle formed by the helix with the horizontal, we have from
the geometry that
z = Rθ tan φ
(3.72)
Suppose now that we make the following substitution:
α ⇌ tan φ
(3.73)
Then the position of the bead can be written as
r = Rer + tan φRθez = Rer + αRθez
(3.74)
Furthermore, the angular velocity of reference frame A in reference frame F is
given as
F A
ω = θ̇ez
(3.75)
Then, differentiating Eq. (3.74) in reference frame F , the velocity of the bead is
given as
F
dr Adr F A
F
v=
=
+ ω ×r
(3.76)
dt
dt
where
A
dr
= αR θ̇ez
dt
(3.77)
F ωA × r = θ̇e × (Re + αRθe ) = R θ̇e
z
r
z
θ
Adding the two expressions in Eq. (3.77), we obtain
F
v = R θ̇eθ + αR θ̇ez
(3.78)
The speed in reference frame F is then given as
F
p
d F s
v = kF vk = R θ̇ 1 + α2 ≡
dt
(3.79)
Consequently,
F
p
ds = R 1 + α2 dθ
(3.80)
Integrating both sides of Eq. (3.80), we obtain
Z Fs
Fs
0
ds =
Zθ
θ0
p
R 1 + α2 dθ
(3.81)
73
We then obtain
F
p
s − F s0 = R 1 + α2 (θ − θ0 )
Solving Eq. (3.82) for s, the arclength is given as
p
F
s = F s0 + R 1 + α2 (θ − θ0 )
(3.82)
(3.83)
Now the tangent vector in reference frame F is given as
et =
Fv
(3.84)
Fv
Using the speed from Eq. (3.79) and the velocity from Eq. (3.78), the tangent
vector in reference frame F is obtained as Substituting the expressions for F v
and F v from part (a) into Eq. (3.84), we obtain
et =
R θ̇eθ + αR θ̇ez
√
R θ̇ 1 + α2
(3.85)
Simplifying Eq. (3.85), we have
eθ + αez
et = √
1 + α2
(3.86)
Next, we have
F
det
= κ F ven
dt
(3.87)
Applying the rate of change transport theorem between reference frames A and
F , we have
F
A
det
det F A
=
+ ω × et
(3.88)
dt
dt
where
A
det
dt
F
ωA × et
= 0
(3.89)
θ̇
eθ + αez
= −√
er
= θ̇ez × √
2
1+α
1 + α2
(3.90)
Adding Eqs. (3.89) and (3.90) gives
F
det
θ̇
er
= −√
dt
1 + α2
(3.91)
The principal unit normal is then given as
en =
F
F
det /dt
k det /dtk
= −er
(3.92)
74
Chapter 3. Kinetics of Particles
We then obtain the principal unit bi-normal vector as
αeθ − ez
eθ + αez
× (−er ) = − √
eb = et × en = √
1 + α2
1 + α2
(3.93)
Furthermore, the curvature is given as
κ=
F
1
det /dt
=
Fv
R(1 + α2 )
(3.94)
The acceleration in reference frame F is then given as
F
a=
2
d F v et + κ F v en
dt
(3.95)
Using the expression for F v from Eq. (3.79) we have that
p
d F v = R θ̈ 1 + α2
dt
(3.96)
Also, using the curvature from Eq. (3.94), we have that
κ
F
v
2
=
h p
i2
1
2
R
θ̇
1
+
α
= R θ̇ 2
R(1 + α2 )
(3.97)
Thus, the acceleration is given as
F
p
a = R θ̈ 1 + α2 et + R θ̇ 2 en
(3.98)
Kinetics
Using the free body diagram in Fig. 3-4, we have that
Nn = Reaction Force of Track on Bead in en Direction
Nb = Reaction Force of Track on Bead in eb Direction
mg = Force of Gravity
Therefore,
Nb
⊗
Nn
mg
Figure 3-4
Free Body Diagram for Question 3.4
F = Nn + Nb + mg
(3.99)
75
From the geometry we have that
Nn
Nb
= Nn en
= Nb en
(3.100)
(3.101)
mg = −mgez
(3.102)
F = Nn en + Nb eb − mgez
(3.103)
Consequently,
Now from Eqs. (3.86) and (3.93) we have
et
eb
eθ + αez
√
1 + α2
αeθ − ez
= −√
1 + α2
=
(3.104)
Using Eq. (3.104) we√can obtain an expression for ez √
in terms of et and eb . First,
multiplying et by α 1 + α2 and multiplying eb by − 1 + α2 , we obtain
√
α 1 + α2 et
√
− 1 + α2 eb
= αeθ + α2 ez
= αeθ − ez
Subtracting these last two equations gives
p
p
α 1 + α2 et + 1 + α2 eb = (1 + α2 )ez
(3.105)
(3.106)
Solving this last equation for ez , we obtain
αet + eb
ez = √
1 + α2
The force F given in Eq. (3.103) can then be written as
αet + eb
√
F = Nn en + Nb eb − mg
1 + α2
Separating this last equation into components, we obtain
mgα
mg
F = −√
eb
et + Nn en + Nb − √
1 + α2
1 + α2
(3.107)
(3.108)
(3.109)
(a) Differential Equation Using Newton’s 2nd Law
Setting F = mF a using the expression for F a from Eq. (3.98), we obtain
p
mgα
mg
−√
et + Nn en + Nb − √
eb = mR θ̈ 1 + α2 et + mR θ̇ 2 en (3.110)
1 + α2
1 + α2
76
Chapter 3. Kinetics of Particles
Equating components in Eq. (3.110) yields the following three scalar equations:
mgα
−√
1 + α2
Nn
Nb
p
= mR θ̈ 1 + α2
= mR θ̇ 2
mg
= √
1 + α2
(3.111)
(3.112)
(3.113)
It is noted that, because it contains no reaction forces, Eq. (3.111) is the differential equation of motion for the particle, i.e., the differential equation of motion
is given as
p
mgα
=0
(3.114)
mR θ̈ 1 + α2 + √
1 + α2
Eq. (3.114) can be rewritten as
mR(1 + α2 )θ̈ + mgα = 0
(3.115)
Simplifying Eq. (3.115), we obtain
θ̈ +
g
α=0
R(1 + α2 )
(3.116)
Then, using the the fact that α = tan φ from Eq. (3.73), we obtain
θ̈ +
g
tan φ = 0
R(1 + tan2 φ)
(3.117)
Now from trigonometry we have that
1 + tan2 φ = sec2 φ
(3.118)
Using the result of Eq. (3.118) in Eq. (3.117), we obtain the differential equation
of motion as
g tan φ
=0
(3.119)
θ̈ +
R sec2 φ
(b) Differential Equation Using Work-Energy Theorem
Applying the work-energy theorem to the bead, we have
d F T = F · Fv
dt
(3.120)
Using the expression for F v from Eq. (3.78), the kinetic energy in reference frame
F is given as
F
T =
1 F
1
1
m v · F v = m(R 2 θ̇ 2 α2 R 2 θ̇ 2 ) = mR 2 (1 + α2 )θ̇ 2
2
2
2
(3.121)
77
Computing the rate of change of kinetic energy, we obtain
d F T = mR 2 (1 + α2 )θ̇ θ̈
dt
(3.122)
Next, using the resultant force acting on the bead as given in Eq. (3.109), the
power produced by all forces is given as
mg
mgα
(3.123)
eb · F v
et + Nn en + Nb − √
F · Fv = − √
1 + α2
1 + α2
Recalling by definition that F v = F vet , Eq. (3.123) simplifies to
mgα F
F · Fv = − √
v
1 + α2
Then, substituting the expression for F v from Eq. (3.79), we have
p
mgα
F · Fv = − √
R θ̇ 1 + α2
1 + α2
(3.124)
(3.125)
Setting Eq. (3.122) equal to Eq. (3.125), we obtain
p
mgα
R θ̇ 1 + α2
mR 2 (1 + α2 )θ̇ θ̈ = − √
1 + α2
Rearranging Eq. (3.126) yields
p
mgα
θ̇ mR 2 (1 + α2 )θ̈ + √
R 1 + α2 = 0
1 + α2
(3.126)
(3.127)
Observing that θ̇ ≠ 0 as a function of time, the differential equation of motion
is obtained as
p
mgα
mR 2 (1 + α2 )θ̈ + √
(3.128)
R 1 + α2 = 0
1 + α2
(c) Maximum Displacement of Bead
For this particular problem, we can obtain the maximum distance traveled using
the alternate form of the work-energy theorm for a particle. In particular, we
know that
d F E = Fnc · F v
(3.129)
dt
Now since the force of gravity is conservative, we know that the only possible
non-conservative forces are due to the reaction of the track on the bead, i.e.,
Fnc = Nn + Nb
(3.130)
Using the expressions for Nn and Nb from Eq. (3.100) and Eq. (3.101), we have
that
Fnc = Nn en + Nb eb
(3.131)
78
Chapter 3. Kinetics of Particles
Furthermore, since en and eb both lie in the direction orthogonal to et , we have
that
en · et = 0
(3.132)
eb · et = 0
Furthermore, since F v = F vet , we know that
Fnc = (Nn en + Nb eb ) · F vet = 0
(3.133)
d F E =0
dt
(3.134)
Consequently,
Integrating Eq. (3.134), we obtain
F
E = constant
(3.135)
Now since F E = F T + F U, we have
F
T + F U = constant
(3.136)
Next, we know that the bead will attain its maximum distance when its velocity is
zero, i.e., the maximum distance will be attained when θ̇ = 0. Using Eq. (3.136),
we have that
F
T0 + F U 0 = F T1 + F U 1
(3.137)
where the subscript “0” is at time t = t0 = 0, and the subscript “1” is at time t =
t1 when θ̇ = 0. We already have the kinetic energy of the bead from Eq. (3.121).
Next, since the only conservative force acting on the bead is due to gravity, the
potential energy of the bead in reference frame F is given as
F
U = F Ug = −mg · r
(3.138)
Substituting the expression for r from Eq. (3.74) and the expression for mg from
Eq. (3.102) into Eq. (3.138), we obtain
F
U = F Ug = mgez · (Rer + αRθez ) = mgRθα
Then, substituting the expression for
into Eq. (3.136), we obtain
F
T and
F
(3.139)
U from Eqs. (3.121) and 3.139
1
mR 2 θ̇ 2 (1 + α2 ) + mgRθα = constant
2
(3.140)
Furthermore, applying Eq. (3.137), we obtain
1
1
mR 2 θ̇02 (1 + α2 ) + mgRθ0 α = mR 2 θ̇12 (1 + α2 ) + mgRθ1 α
2
2
(3.141)
79
Now we know that since the maximum distance is obtained when the velocity of
the bead is zero, we must have that θ̇1 = 0. Furthermore, since the initial value
of θ is zero, we have that θ0 = 0. Consequently, Eq. (3.141) reduces to
1
mR 2 θ̇02 (1 + α2 ) = mgRθ1 α
2
(3.142)
Solving Eq. (3.142) for θ1 , we obtain
θ1 =
R θ̇02 (1 + α2 )
2gα
(3.143)
Finally, since the distance traveled along the helix is equivalent to the arclength,
the distance traveled along the helix is given from Eq. (3.83) as
F
p
R θ̇02 (1 + α2 )
s = R 1 + α2
2gα
(3.144)
Simplifying Eq. (3.144), we obtain the maximum distance traveled along the incline as
3/2
R 2 θ̇02 F
1 + α2
(3.145)
s=
2gα
80
Chapter 3. Kinetics of Particles
Question 3–5
A collar of mass m is constrained to move along a frictionless track in the form
of a logarithmic spiral as shown in Fig. P3-5. The equation for the spiral is given
as
r = r0 e−aθ
where r0 and a are constants and θ is the angle as shown in the figure. Assuming that gravity acts downward, determine the differential equation of motion in
terms of the angle θ using (a) Newton’s 2nd law and (b) the work-energy theorem
for a particle.
θ
m
r
=
r0
e −a
g
O
θ
Figure P 3-5
Solution to Question 3–5
Kinematics
Let F be a reference frame fixed to the track. Then, choose the following coordinate system fixed in reference frame F :
Ex
Ez
Ey
Origin at O
=
=
=
To the Right
Out of Page
Ez × Ex
Next, let A be a reference frame fixed to the direction of Om. Then, we choose
the following coordinate system fixed in reference frame F :
er
Ez
eθ
Origin at O
=
=
=
Along Om
Out of Page
Ez × e r
81
The relationship between the bases {Ex , Ey , Ez } and {er , eθ , ez } is given as
er
eθ
= cos θ Ex + sin θ Ey
= − sin θ Ex + cos θ Ey
(3.146)
(3.147)
The position of the particle is then given as
r = r er = r0 e−aθ er
(3.148)
Furthermore, the angular velocity of reference frame A in reference frame F is
given as
F A
ω = θ̇Ez
(3.149)
Applying the rate of change transport theorem between reference frames A and
F , we obtain the velocity of the particle in reference frame F as
F
v=
F
dr Adr F A
=
+ ω ×r
dt
dt
(3.150)
where
A
dr
= ṙ er = −ar0 θ̇e−aθ er
dt
F A
ω × r = θ̇Ez × r er = θ̇Ez × r0 e−aθ er = r0 θ̇e−aθ eθ
(3.151)
(3.152)
Adding the expressions in Eq. (3.151) and Eq. (3.152), we obtain the velocity of
the particle in reference frame F as
F
v = −ar0 θ̇e−aθ er + r0 θ̇e−aθ eθ
(3.153)
Simplifying Eq. (3.150), we obtain F v as
F
v = r0 θ̇e−aθ [−aer + eθ ]
(3.154)
Now we need the acceleration of the collar in reference frame F . For this problem it is most convenient to obtain F a in terms of an intrinsic basis as viewed
by an observer fixed to the track. First, the tangent vector is given as
et =
Fv
kF vk
=
Fv
kF vk
(3.155)
where F v is the speed of the particle in reference frame F . Now we know that
the speed of the particle in reference frame F is given as
p
F
(3.156)
v = kF vk = r0 θ̇e−aθ a2 + 1
Dividing F v in Eq. (3.154) by F v in Eq. (3.156), we obtain et as
−aer + eθ
et = √
a2 + 1
(3.157)
82
Chapter 3. Kinetics of Particles
Then, the principle unit normal vector is obtained as
en =
F
det /dt
F
k det /dtk
(3.158)
Now we have from the basic kinematic equation that
F
where
F
det
dt
A
det F A
det
=
+ ω × et
dt
dt
= 0
er + aeθ
−aer + eθ
= −θ̇ √
× et = θ̇Ez × √
2
a +1
a2 + 1
Adding the expressions in Eq. (3.160), we obtain
(3.159)
(3.160)
F ωA
F
Consequently,
Dividing
F
er + aeθ
det
= −θ̇ √
dt
a2 + 1
F de t
= θ̇
dt (3.161)
(3.162)
det /dt in Eq. (3.161) by kF det /dtk in Eq. (3.162), we obtain en as
er + aeθ
en = − √
a2 + 1
(3.163)
kF det /dtk
Fv
(3.164)
Furthermore, the curvature, κ, is obtained as
κ=
Substituting kF det /dtk from Eq. (3.162) and F v from Eq. (3.156), we obtain κ
as
1
√
(3.165)
κ=
−aθ
r0 e
a2 + 1
The acceleration is then given in terms of the intrinsic basis as
2
d F F
a=
v et + κ F v en
(3.166)
dt
Now we have that
Furthermore,
2
κ Fv =
p
d F v = r0 (θ̈ − aθ̇ 2 )e−aθ a2 + 1
dt
(3.167)
1
√
(3.168)
r0 e−aθ a2 + 1
p
r02 θ̇ 2 e−2aθ (a2 + 1) = r0 θ̇ 2 e−aθ a2 + 1
The acceleration in reference frame F is then given as
p
p
F
a = r0 e−aθ a2 + 1(θ̈ − aθ̇ 2 )et + r0 θ̇ 2 e−aθ a2 + 1en
(3.169)
83
Kinetics
The free body diagram of the particle is shown in Fig. 3-5. It can be seen that
N
Figure 3-5
mg
Free Body Diagram fof Question 3–5.
the following two forces act on the collar: (1) the reaction force of the track, N,
and (2) gravity, mg. Since N acts in the direction normal to the track, we have
N = Nn en
(3.170)
Now, since gravity acts vertically downward, we have that
mg = −mgEy
(3.171)
where Ey is the vertically upward direction. Resolving Ey in the basis {er , eθ , Ez },
we have that
Ey = sin θ er + cos θ eθ
(3.172)
Consequently, the force of gravity can be written as
mg = −mg sin θ er − mg cos θ eθ
(3.173)
Then the total force acting on the collar is given as
F = N + mg = Nn en − mg sin θ er − mg cos θ eθ
(3.174)
(a) Differential Equation Using Newton’s 2nd Law
Setting F equal to mF a using F a from Eq. (3.169), we obtain
p
Nn en − mg sin θ er − mg cos θ eθ = mr0 e−aθ a2 + 1(θ̈ − aθ̇ 2 )et
p
+ mr0 θ̇ 2 e−aθ a2 + 1en
(3.175)
Now we know that, in order to obtain the differential equation of motion, we
need to eliminate the reaction force exerted by the track. An easy way to
eliminate N is to take the scalar product in the et -direction on both sides of
Eq. (3.175). Noting that en · et = 0, we then obtain
p
−mg sin θ er · et − mg cos θ eθ · et = mr0 e−aθ a2 + 1(θ̈ − aθ̇ 2 )
(3.176)
84
Chapter 3. Kinetics of Particles
Now, using the expression for et from Eq. (3.157) and the expression for en from
Eq. (3.163), we have that
er · et
eθ · et
a
−aer + eθ
= −√
= er · √
2
2
a +1
a +1
−aer + eθ
1
= eθ · √
=√
2
2
a +1
a +1
(3.177)
Substituting the expressions in Eq. (3.177) into Eq. (3.176), we obtain
mg sin θ √
a
a2 + 1
− mg cos θ √
1
a2 + 1
p
= mr0 e−aθ a2 + 1(θ̈ − aθ̇ 2 )
(3.178)
Rearranging and simplifying Eq. (3.178), we obtain the differential equation of
motion as
g
θ̈ − aθ̇ 2 +
(3.179)
eaθ (cos θ − a sin θ ) = 0
r0 (a2 + 1)
(b) Differential Equation Using Work-Energy Theorem for a Particle
To obtain the differential equation of motion using the work-energy, we choose
to apply the alternate form of the work-energy theorem for a particle. The
alternate form of the work-energy theorem is given in reference frame F as
d F E = Fnc · F v
dt
(3.180)
Now for this problem we know that the only two forces acting on the particle are
the force of gravity and the reaction force of the track. Moreover, we know that
the force of gravity is conservative while the reaction force is non-conservative.
Therefore, we have Fnc as
Fnc = N
(3.181)
Now, since N acts in the direction of en and F v acts in the direction of et , we
have that
Fnc · F v = N · F v = Nen · F vet = 0
(3.182)
Consequently,
d F E =0
dt
(3.183)
Now the total energy in reference frame F is given as
F
E = FT + FU
(3.184)
First, the kinetic in reference frame F is given as
F
T =
1 F
m v · Fv
2
(3.185)
85
Using the expression for
reference frame F as
F
Fv
from Eq. (3.154), we obtain the kinetic energy in
1 m r0 θ̇e−aθ [−aer + eθ ] · r0 θ̇e−aθ [−aer + eθ ]
2
1
= mr02 (a2 + 1)θ̇ 2 e−2aθ
2
T =
(3.186)
Next, since gravity is the only conservative force acting on the particle, the potential energy in reference frame F is given as
F
U = F Ug
(3.187)
Now since gravity is a constant force, we have that
F
Ug = −mg · r
(3.188)
Using the expression for r from Eq. (3.148) and the expression for mg from
Eq. (3.171), we obtain F Ug as
F
Ug = −mg · r = −(−mgEy ) · r0 e−aθ er = mgr0 e−aθ Ey · er
(3.189)
Using the expression for er from Eq. (3.146), we have that
Ey · er = Ey · (cos θ Ex + sin θ Ey ) = sin θ
(3.190)
Consequently, F Ug can be written as
F
Ug = mgr0 e−aθ sin θ
(3.191)
Then, adding Eq. (3.186) and Eq. (3.191), the total energy in reference frame F
is given as
F
E = FT + FU =
1
mr02 (a2 + 1)θ̇ 2 e−2aθ + mgr0 e−aθ sin θ
2
(3.192)
Then, computing the rate of change of F E, we obtain
h
i
d F E = mr02 (a2 + 1) θ̇ θ̈e−2aθ = aθ̇ 2 θ̇e−2aθ
dt
h
i
+ mgr0 −aθ̇e
−aθ
sin θ + θ̇e
−aθ
(3.193)
cos θ
Eq. (3.193) can be re-written as
h
i
d F E = mr02 (a2 + 1)θ̇e−2aθ θ̈ − aθ̇ 2 + mgr0 θ̇e−aθ (−a sin θ + cos θ )
dt
(3.194)
86
Chapter 3. Kinetics of Particles
Simplifying Eq. (3.194) and setting the result equal to zero, we obtain
h
i
d F E = θ̇ mr02 (a2 + 1)e−2aθ (θ̈ − aθ̇ 2 ) + mgr0 e−aθ (cos θ − a sin θ ) = 0
dt
(3.195)
Now since θ̇ ≠ 0 as a function of time (otherwise the particle would not be
moving), the term in the square brackets must be zero, i.e.,
mr02 (a2 + 1)e−2aθ (θ̈ − aθ̇ 2 ) + mgr0 e−aθ (cos θ − a sin θ ) = 0
(3.196)
Then, dividing Eq. (3.196) by mr02 (a2 + 1)e−2aθ , we obtain the differential equation of motion as
θ̈ − aθ̇ 2 +
g
eaθ (cos θ − a sin θ ) = 0
r0 (a2 + 1)
(3.197)
It is seen that the result of Eq. (3.197) is identical to that obtained in part (a).
87
Question 3–7
A particle of mass m slides without friction along the inner surface of a fixed
cone of semi-vertex angle β as shown in the Fig. P3-7. The equation for the cone
is given in cylindrical coordinates as
z = r cot β
Knowing that the basis {Ex , Ey , Ez } is fixed to the cone, that θ is the angle between the Ex -direction and the direction OQ where Q is the projection of the
particle into the {Ex , Ey }-plane, and that gravity acts vertically downward, determine a system of two differential equations in terms of r and θ that describe
the motion of the particle.
Ez
g
m
β
P
O
Ey
θ
r
Q
Ex
Figure P 3-7
Solution to Question 3–7
Kinematics
First, let F be a reference frame fixed to the cone. Then, choose the following
coordinate system fixed in reference frame F :
Ex
Ey
Ez
Origin at O
=
=
=
As Given
As Given
Ex × Ey = As Given
Next, let A be a reference frame fixed to the plane formed by the points O, Q,
and P . Then, choose the following coordinate system fixed in reference frame
88
Chapter 3. Kinetics of Particles
A:
er
ez
eθ
Origin at O
=
=
=
Along OQ
Ez
Ez × er
The position of the particle is then given as
r = r er + zez = r er + r cot βez
(3.198)
Furthermore, the angular velocity of reference frame A in reference frame F is
given as
F A
ω = θ̇Ez
(3.199)
The velocity of the particle in reference frame F is then obtained from the rate
of change transport theorem as
F
v=
F
dr Adr F A
=
+ ω ×r
dt
dt
(3.200)
Now we have that
A
dr
= ṙ er + ṙ cot βez
dt
F A
ω × r = θ̇ez × (r er + r cot βez ) = r θ̇eθ
(3.201)
(3.202)
Adding the expressions in Eq. (3.201) and Eq. (3.202), we obtain the velocity of
the particle in reference frame F as
F
v = ṙ er + r θ̇eθ + ṙ cot βez
(3.203)
Next, applying the rate of change transport theorem to F v, we obtain the acceleration of the particle in reference frame F as
F
a=
d F Ad F F A F
v =
v + ω × v
dt
dt
F
(3.204)
Now we have that
A
d F v
= r̈ er + (ṙ θ̇ + r θ̈)eθ + r̈ cot βez
(3.205)
dt
F A
ω × F v = θ̇Ez × ṙ er + r θ̇eθ + ṙ cot βEz = ṙ θ̇eθ − r θ̇ 2 er (3.206)
Adding the expressions in Eq. (3.205) and Eq. (3.206), we obtain the acceleration
of the particle in reference frame F as
F
a = (r̈ − r θ̇ 2 )er + (r θ̈ + 2ṙ θ̇)eθ + r̈ cot βez
(3.207)
89
N
m
mg
Figure 3-6
Free Body Diagram of Particle for Question 3–7.
Kinetics
In order to determine the differential equations of motion, we need to apply
Newton’s 2nd Law, i.e., we need to apply F = mF a. The free body diagram of
the particle is shown in Fig. 3-6. Using Fig. 3-6, we see that the only two forces
acting on the particle are
N
= Reaction Force of Cone on Particle
mg = Force of Gravity
Since we now that N must lie in the direction orthogonal to the surface of the
cone while the force of gravity acts vertically downward, we can write N and
mg, respectively, as
N = Nn
mg = −mgez
(3.208)
(3.209)
where n is the direction orthogonal to the surface of the cone at the location of
the particle. Now we know that the direction orthogonal to the surface of the
cone is the same as the direction of the gradient of the function that describes
the cone. In particular, the function that describes the surface of the cone is
given as
z = r cot β
(3.210)
Rearranging Eq. (3.210), the function that describes the surface of the cone is
given in cylindrical coordinates as
f (r , θ, z) = z − r cot β = 0
(3.211)
The gradient of f in cylindrical coordinates is then given as
∇f =
∂f
1 ∂f
∂f
er +
eθ +
ez
∂r
r ∂θ
∂z
(3.212)
90
Chapter 3. Kinetics of Particles
where
∂f
∂r
∂f
∂θ
∂f
∂z
We then obtain ∇f as
= − cot β
(3.213)
= 0
(3.214)
= 1
(3.215)
∇f = − cot βer + ez
(3.216)
The unit normal to the surface of the cone is then given as
n=
− cot βer + ez
∇f
= q
k∇f k
1 + cot2 β
(3.217)
Now from trigonometry we have that
1 + cot2 β = csc2 β = 1/ sin2 β
(3.218)
Substituting the result of Eq. (3.218) into Eq. (3.217), we obtain the unit normal
to the surface of the cone as
n = sin β(− cot βer + ez ) = − cos βer + sin βez
(3.219)
Then, substituting the expression for n from Eq. (3.219) into Eq. (3.208), we
obtain the reaction force of the cone on the particle as
N = N(− cos βer + sin βez ) = −N cos βer + N sin βez
(3.220)
The resultant force on the particle is then given as
F = N + mg = −N cos βer + N sin βez − mgez = −N cos βer + (N sin β − mg)ez
(3.221)
Setting F in Eq. (3.221) equal to mF a using the expression for F a from Eq. (3.207),
we have that
−N cos βer + (N sin β − mg)ez = m(r̈ − r θ̇ 2 )er + m(r θ̈ + 2ṙ θ̇)eθ + mr̈ cot βez
(3.222)
Equating components in Eq. (3.222), we obtain the following three scalar equations:
−N cos β = m(r̈ − r θ̇ 2 )
0 = m(r θ̈ + 2ṙ θ̇)
N sin β − mg
= mr̈ cot β
(3.223)
(3.224)
(3.225)
91
Now, it is seen that Eq. (3.224) has no unknown reaction forces. Consequently,
Eq. (3.224) is one of the differential equations of motion. Dropping m from
Eq. (3.224), the first differential equation of motion can be written as
r θ̈ + 2ṙ θ̇ = 0
(3.226)
The second differential equation of motion can be obtained using Eq. (3.223)
and Eq. (3.223). In particular, we can rearrange Eq. (3.225) as
N sin β = mr̈ cot β + mg
(3.227)
Then, dividing Eq. (3.227) by Eq. (3.223), we obtain
mr̈ cot β + mg
N sin β
=
−N cos β
m(r̈ − r θ̇ 2 )
(3.228)
Eq. (3.228) simplifies to
tan β = −
Rearranging Eq. (3.229) gives
r̈ cot β + g
(3.229)
r̈ − r θ̇ 2
(r̈ − r θ̇ 2 ) tan β = −r̈ cot β − g
(3.230)
Then, dividing Eq. (3.230) by tan β, we obtain
(r̈ − r θ̇ 2 ) = r̈ cot2 β + g cot β = 0
(3.231)
Rearranging Eq. (3.231) gives
(1 + cot2 β)r̈ − r θ̇ 2 + g cot β = 0
(3.232)
Once again, using the fact that 1 + cot2 β = csc2 β, Eq. (3.232) simplifies to
csc2 βr̈ − r θ̇ 2 + g cot β = 0
(3.233)
Dividing Eq. (3.233) by csc2 β, we obtain the second differential equation of motion as
r̈ − r θ̇ 2 sin2 β + g cos β sin β = 0
(3.234)
The two differential equations that govern the motion of the particle are then
given from Eq. (3.226) and Eq. (3.234) as
2
2
r θ̈ + 2ṙ θ̇
= 0
r̈ − r θ̇ sin β + g cos β sin β = 0
(3.235)
(3.236)
92
Chapter 3. Kinetics of Particles
Question 3–9
A particle of mass m is attached to one end of a flexible but inextensible massless rope as shown in Fig. P3-9. The rope is wrapped around a cylinder of radius
R where the cylinder rotates with constant angular velocity Ω relative to the
ground. The rope unravels from the cylinder in such a manner that it never
becomes slack. Furthermore, point A is fixed to the cylinder and corresponds
to a configuration where no portion of the rope is exposed while point B is the
instantaneous point of contact of the exposed portion of the rope with the cylinder. Knowing that the exposed portion of the rope is tangent to the cylinder
at every instant of the motion, that θ is the angle between points A and B, and
assuming the initial conditions θ(t = 0) = 0, θ̇(t = 0) = Ω (where Ω = kΩk),
determine (a) the angular velocity of the exposed portion of the rope as viewed
by an observer fixed to the ground, (b) the acceleration of the particle as viewed
by an observer fixed to the ground, (c) the differential equation for the particle
in terms of the variable θ, and (d) the tension in the rope as a function of time.
m
P
B
θ
A
O
R
Ω
Figure P 3-9
Solution to Question 3–9
Kinematics
First, let F be a reference frame that is fixed in the ground. Then, choose the
following coordinate system fixed in reference frame F :
Ex
Ez
Ey
Origin at O
=
=
=
Along OA at t = 0
Out of Page
Ez × Ex
93
Next, let A be a reference frame fixed to the cylinder. Then, choose the following
coordinate system fixed in reference frame A:
ux
uz
uy
Origin at O
=
=
=
Along OA
Out of Page
uz × ux
Finally, let B be a reference frame fixed to the rope. Then, choose the following
coordinate system fixed in reference frame B:
ex
ez
ey
Origin at B
=
=
=
Along OB
Out of Page
ez × ex
Now, we note that the cylinder rotates with constant angular velocity Ω
about the uz -direction. Consequently, the angular velocity of the cylinder in
reference frame F is given as
F
ωA = Ω = Ωuz
(3.237)
Next, since A is fixed in the cylinder and B is fixed in the rope, the angular
velocity of the rope relative to the cylinder is equivalent to the angular velocity
of reference frame B relative to reference frame A. Observing from Fig. 3-7 that
θ defines the rotation of the rope relative to the cylinder, we have that
A
ωB = θ̇ez
(3.238)
Then, applying the angular velocity addition theorem, the angular velocity of
the rope relative to the ground is obtained by adding the results of Eq. (3.237)
and Eq. (3.238) to obtain
F
ωB = F ωA + A ωB = Ωuz + θ̇ez = (Ω + θ̇)ez
(3.239)
where we note that uz = ez . Next, we know that, when no portion of the rope is
exposed (i.e., s = 0), the particle is in contact with point A on the cylinder. Using
Fig. 3-7 along with the fact that the cylinder is circular, the arclength along the
cylinder from point A to point B is given as
s = Rθ
(3.240)
Differentiating Eq. (3.240), we obtain
ṡ = R θ̇
(3.241)
Next, the position of the particle is given in terms of the basis {ex , ey , ez } as
r = Rex − sey = Rex − Rθey
(3.242)
94
Chapter 3. Kinetics of Particles
s=
Rθ
m
θ
B
A
R
O
Figure 3-7
Geometry of Rope and Cylinder for Question 3–9.
The velocity of the particle in reference frame F is then given as
F
v=
F
dr Bdr F B
=
+ ω ×r
dt
dt
(3.243)
where
B
dr
dt
= −R θ̇ey
F B
ω ×r =
Ω + θ̇ ez × Rex − Rθey
= Rθ Ω + θ̇ ex + R Ω + θ̇ ey
(3.244)
(3.245)
Adding the expressions in Eq. (3.244) and Eq. (3.245), we obtain the velocity of
the particle in reference frame F as
F
v = −R θ̇ey + Rθ Ω + θ̇ ex + R Ω + θ̇ ey
(3.246)
Simplifying Eq. (3.246), we obtain
F
v = Rθ Ω + θ̇ ex + RΩey
(3.247)
Then, the acceleration in reference frame F is given as
F
v=
F
d F B d F F B F
v =
v + ω × v
dt
dt
(3.248)
where
B
h
i
d F v
=
R θ̇ Ω + θ̇ + Rθ θ̈ ex
dt
i
h
F B
ω × Fv =
Ω + θ̇ ez × Rθ Ω + θ̇ ex + RΩey
(3.249)
95
2
= −RΩ Ω + θ̇ ex + Rθ Ω + θ̇ ey
(3.250)
Adding Eq. (3.249) and Eq. (3.250), we obtain the acceleration of the particle in
reference frame F
F
h
i
2
a = R θ̇ Ω + θ̇ + Rθ θ̈ ex − RΩ Ω + θ̇ ex + Rθ Ω + θ̇ ey
(3.251)
Simplifying Eq. (3.251
F
h
i
2
a = R θ̇ 2 + Rθ θ̈ − RΩ2 ex + Rθ Ω + θ̇ ey
(3.252)
Kinetics and Differential Equation of Motion
We need to apply Newton’s 2nd law to the particle. Using the free body diagram
as shown in Fig. 3-8, it can be seen that the only force acting on the particle is
due to the tension in the rope. Since the tension must act along the direction of
the rope, we have that
T = T ey
(3.253)
Therefore, the resultant force acting on the particle is given as
m
T
Figure 3-8
Free Body Diagram for Question 3.5
F = T = T ey
(3.254)
Setting F = mF a using F a from Eq. (3.252), we obtain
i
2
h
T ey = m R θ̇ 2 + Rθ θ̈ − RΩ2 ex + mRθ Ω + θ̇ ey
We then obtain the following two scalar equations:
h
i
m R θ̇ 2 + Rθ θ̈ − RΩ2
= 0
2
mRθ Ω + θ̇
= T
(3.255)
(3.256)
(3.257)
From Eq (3.256) we have
R θ̇ 2 + Rθ θ̈ − RΩ2 = 0
(3.258)
Simplifying this last expression, we obtain the differential equation of motion
as
θ̇ 2 + θ θ̈ − Ω2 = 0
(3.259)
96
Chapter 3. Kinetics of Particles
Tension in Rope As a Function of Time
Eq. (3.259) can be solved for θ. This is done as follows. First, we note that
θ̇ 2 + θ θ̈ =
d θ θ̇
dt
(3.260)
Substituting this last result into Eq. (3.259), we obtain
d θ θ̇ − Ω2 = 0
dt
(3.261)
Integrating Eq. (3.261) once with respect to time, we obtain
θ θ̇ = Ω2 t + c1
(3.262)
where c1 is an arbitrary constant of integration. Then, applying the initial condition θ(t = 0) = 0, we have that
c1 = 0
(3.263)
θ θ̇ = Ω2 t
(3.264)
Therefore, we have
Then, separating variables in Eq. (3.264), we obtain
θdθ = Ω2 tdt
(3.265)
Integrating both sides of Eq. (3.265) gives
θ2
Ω2 t 2
=
+ c2
2
2
(3.266)
where c2 is an arbitrary constant of integration. Then, again applying the initial
condition θ(t = 0) = 0, we obtain
c2 = 0
(3.267)
Ω2 t 2
θ2
=
2
2
(3.268)
θ 2 = Ω2 t 2
(3.269)
Consequently,
which gives
Since θ has to be positive, we can take the principal square root of Eq. (3.269)
to obtain
θ = Ωt
(3.270)
Differentiating with respect to time, we have
θ̇ = Ω
(3.271)
97
Then, substituting θ from Eq. (3.270) and θ̇ from Eq. (3.271) into Eq. 3.257 gives
T = mRΩt (Ω + Ω)2 = 4mRΩ3 t
The tension in the rope is then given as
h
i
T = 4mRΩ3 t ey
(3.272)
(3.273)
98
Chapter 3. Kinetics of Particles
Question 3–10
A particle of mass m moves under the influence of gravity in the vertical plane
along a track as shown in Fig. P3-10. The equation for the track is given in
Cartesian coordinates as
y = − ln cos x
where −π /2 < x < π /2. Using the horizontal component of position, x, as the
variable to describe the motion determine the differential equation of motion
for the particle using (a) Newton’s 2nd law and (b) one of the forms of the workenergy theorem for a particle.
Ey
g
m
y = − ln cos x
O
Ex
Figure P 3-10
Solution to Question 3–10
Kinematics
For this problem, it is convenient to use a reference frame F that is fixed to the
track. Then, we choose the following coordinate system fixed in reference frame
F:
Origin at O
Ex
=
Along Ox
Ey
=
Along Oy
Ez
=
Ex × Ey
The position of the particle is then given as
r = xEx − ln cos xEy
(3.274)
Now, since the basis {Ex , Ey , Ez } does not rotate, the velocity in reference frame
F is given as
F
v = ẋEx + ẋ tan xEy
(3.275)
Using the velocity from Eq. (3.275), the speed of the particle in reference frame
F is given as
q
F
F
v = k vk = ẋ 1 + tan2 x = ẋ sec x
(3.276)
99
Arclength Parameter as a Function of x
Now we recall the arclength equation as
q
d F F
s = v = ẋ 1 + tan2 x = ẋ sec x
dt
(3.277)
Separating variables in Eq. (3.277), we obtain
F
ds = sec xdx
(3.278)
Integrating both sides of Eq. (3.278) gives
Zx
F
F
sec xdx
s − s0 =
(3.279)
x0
Using the integral given for sec x, we obtain
F
F
s − s0 = ln [sec x
+ tan x]x
x0
sec x + tan x
= ln
sec x0 + tan x0
(3.280)
Noting that F s(0) = F s0 = 0, the arclength is given as
F
s = ln [sec x + tan x]x
x0
(3.281)
Simplifying Eq. (3.281), we obtain
F
s = ln
sec x + tan x
sec x0 + tan x0
(3.282)
Intrinsic Basis
Next, we need to compute the intrinsic basis. First, we have the tangent vector
as
Fv
ẋ(Ex + tan xEy )
tan x
1
Ex +
Ey
(3.283)
=
et = F =
sec x
sec x
ẋ sec x
v
Now we note that sec x = 1/ cos x. Therefore,
tan x
= sin x
sec x
(3.284)
et = cos xEx + sin xEy
(3.285)
Eq. (3.283) then simplifies to
Next, the principle unit normal is given as
F
det
= κ F ven
dt
(3.286)
100
Chapter 3. Kinetics of Particles
Differentiating et in Eq. (3.285), we obtain
F
det
= −ẋ sin xEx + ẋ cos xEy
dt
(3.287)
Consequently,
F de t
= ẋ = κ F v
dt which implies that
F
−ẋ sin xEx + ẋ cos xEy
det /dt
=
en = = − sin xEx + cos xEy
F
ẋ
det /dt (3.288)
(3.289)
Then, using F v from Eq. (3.276), we obtain the curvature as
κ=
1
ẋ
=
= cos x
ẋ sec x
sec x
(3.290)
Finally, the principle unit bi-normal is given as
eb = et × en = (cos xEx + sin xEy ) × (− sin xEx + cos xEy ) = Ez
(3.291)
Differential Equation of Motion in Terms of x
The differential equation of motion is obtained using Newton’s 2nd Law for a
particle. First we obtain F using the free body diagram shown below: Using the
N
mg
free body diagram, we can see that
N
= Nen
mg = −mgEy
Therefore, the resultant force acting on the particle is
F = N + mg = Nen − mgEy
(3.292)
Next, the acceleration is given in the intrinsic basis as
F
a=
d F v et + κ F v en
dt
(3.293)
101
Now, using F v from Eq. (3.276), we obtain d(F v)/dt as
h
i
d F v = ẍ sec x + ẋ 2 sec x tan x = sec x ẍ + ẋ 2 tan x
dt
Then, using κ from Eq. (3.290) we obtain
κ F v = cos x(ẋ sec x)2 = ẋ 2 sec x
The acceleration of the particle in reference frame F is then given as
h
i
F
a = sec x ẍ + ẋ 2 tan x et + ẋ 2 sec xen
(3.294)
(3.295)
(3.296)
Setting F from Eq. (3.292) equal to mF a using F a from Eq. (3.296), we obtain
h
i
Nen − mgEy = m sec x ẍ + ẋ 2 tan x et + mẋ 2 sec xen
(3.297)
Now we can take the scalar products on both sides of Eq. (3.297) in the et and
en directions. Taking the scalar product on both sides of Eq. (3.297) in the
et -direction, we obtain
i
h
(3.298)
−mgEy · en = m sec x ẍ + ẋ 2 tan x
Taking the scalar product on both sides in the en -direction, we obtain
N − mgEy · en = mẋ 2 sec x
(3.299)
= Ey · (cos xEx + sin xEy ) = sin x
= Ey · (− sin xEx + cos xEy ) = cos x
(3.300)
Now we note that
Ey · et
Ey · en
Substituting Ey · et and Ey · en into Eq. (3.298) and Eq. (3.299), respectively, we
obtain the following two scalar equations:
m sec x ẍ + ẋ 2 tan x = −mg sin x
(3.301)
mẋ 2 sec x
= N − mg cos x
Seeing that the first equation in Eq. (3.301) has no reaction forces, the differential equation of motion of the particle is given as
h
i
m sec x ẍ + ẋ 2 tan x = −mg sin x
(3.302)
Eq. (3.302) can be rearranged to give
ẍ sec x + ẋ 2 sec x tan x + g sin x = 0
(3.303)
102
Chapter 3. Kinetics of Particles
Question 3–11
A particle of mass m moves in the horizontal plane as shown in Fig. P3-11. The
particle is attached to a linear spring with spring constant K and unstretched
length ℓ while the spring is attached at its other end to the fixed point O. Assuming no gravity, (a) determine a system of two differential equations of motion
for the particle in terms of the variables r and θ, (b) show that the total energy
of the system is conserved, and (c) show that the angular momentum relative to
point O is conserved.
O
r
K
m
θ
Figure P 3-11
Solution to Question 3–11
Acceleration of Particle
First, let F be a reference frame fixed to the ground. Next, let A be a reference
frame that is fixed to the direction Om. Corresponding to reference frame A, we
choose the following coordinate system to describe the motion of the particle:
er
Ez
eθ
Origin at O (Corner)
=
Along Om
=
Out of Page
=
Ez × er
The position of the particle is then given as
r = r er
(3.304)
Now the angular velocity of reference frame A in reference frame F is given as
F
ωA = θ̇Ez
(3.305)
103
The velocity in reference frame F is computed from the rate of change transport
theorem as
F
dr Adr F A
F
=
+ ω ×r
(3.306)
v=
dt
dt
where
Adr
dt
= ṙ er
F ωA
(3.307)
× r = θ̇Ez × r er = r θ̇eθ
Adding the two expressions in Eq. (3.307), we obtain F v as
F
v = ṙ er + r θ̇eθ
Applying the rate of change transport theorem to
particle in reference frame F is given as
F
a=
(3.308)
F v,
the acceleration of the
d F Ad F F A F
v =
v + ω × v
dt
dt
F
(3.309)
where
Ad
dt
Fv
F ωA
= r̈ er + (ṙ θ̇ + r θ̈)eθ
× F v = θ̇Ez × (ṙ er + r θ̇eθ ) = −r θ̇ 2 er + ṙ θ̇eθ
(3.310)
Adding the two expressions in Eq. (3.310), we obtain F a as
F
a = (r̈ − r θ̇ 2 )er + (r θ̈ + 2ṙ θ̇)eθ
(3.311)
System of Two Differential Equations
To obtain a system of two differential equations, we need to apply Newton’s
2nd Law to the particle. We already have F a from Eq. (3.311). Next, in order
to obtain an expression for the resultant force, F, we need to examine the free
body diagram as shown in Fig. 3-9 where Fs is the force due to the spring. Now
Fs
Figure 3-9
Free Body Diagram for Question 2.10.
we note that the general form for the force of a linear spring is
Fs = −K(ℓ − ℓ0 )us
(3.312)
104
Chapter 3. Kinetics of Particles
Now since the attachment point of the spring for this problem is rA = 0, we
have that
ℓ = kr − rA k = krk = r
(3.313)
Furthermore, the direction us is given as
us =
r er
r − rA
=
= er
kr − rA k
r
(3.314)
Finally, the unstretched length of the spring is given as
ℓ0 = L
(3.315)
Therefore, we obtain the spring force as
Fs = −K (r − L) er
(3.316)
Next, since the only force acting on the particle is that of the spring, we can set
Fs from Eq. (3.316) equal to mF a from Eq. (3.311) to give
−K [r − L] er = m(r̈ − r θ̇ 2 )er + m(r θ̈ + 2ṙ θ̇)eθ
(3.317)
Equating components, we obtain the following two scalar equations:
m(r̈ − r θ̇ 2 )
= −K [r − L]
m(r θ̈ + 2ṙ θ̇) =
0
(3.318)
Since there are no reaction forces in either of the equations in Eq. (3.318), these
two equations are the differential equations of motion for the particle.
Conservation of Energy
From the work-energy theorem for a particle, we have that
d F E = Fnc · F v
dt
(3.319)
For this problem, the only force acting on the particle is that of the linear spring.
Since the spring force is conservative, we have that Fnc = 0. Therefore,
d F E =0
dt
(3.320)
which implies that
F
E = constant
which implies that energy is conserved.
(3.321)