* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Significant Figures
Survey
Document related concepts
Transcript
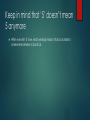
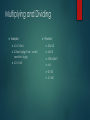
Significant Figures (HOW TO KNOW WHICH DIGITS OF A NUMBER ARE IMPORTANT) How Accurately Can You Measure with This? Could you find measurements like this? 1 inch 2.5 inches 3.1 inches 4.6348 inches Accuracy We want our numbers to convey the level of accuracy we had when measuring Math operations can lead to problems with this: 1.0/3.0 = 0.33333333333333333333333 (The answer looks a lot more precise than the numbers we started with) So, we keep track of the number of significant digits we start with, and use it to round our answer. 1.0/3.0 = 0.33 Rules for Significant Digits Count the number of digits: 45.1 = 3 sig figs 612 = 3 sig figs 9.12345 = 6 sig figs Zeroes are tricky: .0000005 NOT significant 6300 NOT Significant 6300. Significant 705 Significant (Try putting the number in scientific notation, if the zeroes go away, they’re not significant) Practice with Zeroes How many significant figures do each of these numbers have? 5437.2 890 650.0 85 80 .0098 6.004 0.008 602 More Practice: 5,067 4,080 9.01 .01 .00302 10.004 6.120 Math With Significant Figures Adding / Subtracting Multiplying / Dividing Look at all the numbers you started with. Look at the numbers you started with. Find the one with the least number of digits after the decimal place. Find the one with the least number of significant digits. Round your answer to that number of decimal places. Round your answer to that number of significant digits Adding/Subtracting Example: 42.0 + .13 = 42.13 42.0 has one digit after the decimal, .13 has two, so I’ll round the answer to 1 digit after the decimal. Answer: 42.1 That means this is true: 5 + .4 = 5 Why? Keep in mind that ‘5’ doesn’t mean 5 anymore When we write ‘5’ now, what we really mean is that our number is somewhere between 4.5 and 5.4. Adding and Subtracting Practice 4.12 + .1 = 520 + .02 = 12 + 5.1 = 36.8 – 4 = 5.34 - .2 = Multiplying and Dividing Example: Practice: 5.2 x 7 = 36.4 .03 x 5.21 5.2 has 2 sig figs, 7 has 1, so we’ll round it to 1 sig fig 6.2 x 10 5.780 x 2.0617 6 x .1 92 / .03 12 / 4.01 5.2 x 7 = 40