Download Electric Fields and Potentials

NORTHERN ILLINOIS UNIVERSITY
PHYSICS DEPARTMENT
Physics 211 – E&M and Quantum Physics
Fall 2016
Lab #2: Electric Fields and Equipotentials
Lab Writeup Due: Mon/Wed/Fri, Sept. 26/28/29, 2016
Background
“Field forces” describe how an object with certain properties interacts with other objects.
You’ve learned that a “net” force results in an acceleration (Newton’s 2nd law).
You have already worked with the gravitational force fields, especially with objects near the
earth’s surface. You can imagine that every point in space near the earth has an associated
gravitational field vector g, which is the gravitational acceleration that a test body placed at
that point and released, would experience. If m is the mass of the body and F the
gravitational force ("weight") acting on it, g is given by
g  F / m (Newton/kg)
Note that the units of the gravitational force field are Newtons per unit mass, which are also
the units for acceleration.
Gravitational fields surrounds all objects with mass but can only be detected by placing
another object with mass at some distance away and measuring the gravitation field force (or
calculating it using Newton’s law of gravity and then dividing by the mass of the second
object).
Similarly, the space surrounding an electrically charged object (an object with a net electrical
charge) is affected by the object, and we define an electric field being produced by the
charged object.
The objective of this experiment is that you gain some experience with electric fields by
finding the equipotential lines between different electrode shapes, and infer the location
of electric field lines using the properties of both equipotentials and electric fields.
1. Overview
Just like the gravitational field, we must use a “test” charge to measure the electric field. The
electric field vector E is determined by placing a small object carrying a net test charge q 0
(by convention assumed positive) at the point in space that is to be examined and measuring
the electrical force Fe that acts on this test charge. The electrical field vector E at the point
LEAP © 2012 Note: This material was adapted from the “LEAP” project developed by Tennessee
Tech University
is defined as:
E
Fe / q 0 (Newtons/Coulomb)
Where we have divided the Fe by the test charge to find the E .
Note that the units of the electrical force field are Newtons per Coulomb, or force per unit
charge, which parallels the definition of the gravitational force field.
These concepts are summarized in the table below:
Force
Force field vector
Gravity
GM1m2
Fg =
r2
F
g g
m
Electrical
Qq
Fe = ke 12 2
r
F
E e
q
Potential Energy—Another electrostatic comparison to gravity is the concept of
potential energy. Gravitational potential energy is generally based on the distance (between
an object and a gravitational reference point (where gravitational potential energy is zero),
e.g. the height of a ball above the floor. A topographical map shows contour lines that are at
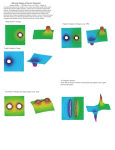
the same gravitational potential level (typically height compared to sea level).
An example below shows an impact crater. All the points on each “squiggly” line circling the
crater are at the same gravitational potential/height. Note that gravitational potential energy
is a property of an object with mass at some height above sea level:
Figure 1—Topographical (contour) map showing gravitational equipotential lines.
Similarly, all the points along each electrical equipotential line have the same electric
potential energy U E , as shown in the figure below:
2
Figure 2—Single electrical positive charge with electric field vectors and equipotential lines (blue dashed).
The difference in the electrical potential energy of any point B from that of any point A in
an electric field is equal to the work W , required to transport a unit positive charge, q 0 from
A to B .
Again, think about the similarities to the gravitational potential energy of a ball when you lift
it against gravity.
Work can be expressed using a quantity V and q 0 , i.e., W
q 0V , where V is simply the
energy per unit charge, or V W / q 0 . V is called the electric potential and is measured in
Joules/Coulombs = volts. The electric potential is a scalar.
Recall that work is proportional to force displacement: W FEd . Work results in a
change in electrical potential energy, which we can relate to electrical force:
W
UE
FEd
and then to the electric field (using FE
FEd
W
V
Ed
qE )
q V
qEd
then
So, the magnitude of the change in electric potential equals the the electric field distance,
the relation above shows that the electric field points in the direction of DECREASING
electric potential.
Now, let’s go back to this charge configuration below: the V between each of the circular
blue equipotential line is the same.
The distances between each successive equipotential lines increases with distance from the
charge because the magnitude of the E field is decreasing by 1 / r 2 , so if V is a constant,
the distance must increase so the product of Ed is constant.
3
An equipotential surface, or contour of constant potential, is simply all points that have the
same electric potential. Thus, the work required to convey a unit positive charge from any
point in one such surface to any point in another is equal to the difference in the potential
energies of the two surfaces, or equal numerically to the difference in potential of the two
surfaces.
Think of a set of stair steps and moving an object up the stairs. Each step is at a different
gravitational potential energy relative to the floor, but moving the ball horizontally along one
step doesn’t change this gravitational potential energy making each step an equipotential
surface. It is obvious that the gravitational force vector g points vertically down,
perpendicular to the equipotential steps. Similarly, the electric force vector E , points
perpendicular to the electric equipotential lines.
2. Procedure
A. Simulation
Find the “P211 Lab Simulations” folder on the lab computer desktop. Run the simulation
software in the folder titled “Electric Fields_equipotentials” on your lab computer. Double
click the “Start.html” icon to start the program (you may get a “Blocked Content” message in
a horizontal bar within Internet Explorer—just click “Allow blocked content”.
Explore different charge configurations like double charge, dipole charge, etc. Use the Help
file to determine the definitions of the terms in the third option (Show—E….) to understand
the visual displays (green arrows, white lines, etc.). Use the slider controls to get different
views.
4
1. Are the distances between the equipotential lines produced by a charge the same? If not,
describe the pattern you observe:
_____________________________________________________________________
_____________________________________________________________________
2. What do you notice about the relationship between the direction of the electric field lines
and the equipotential lines?
______________________________________________________________________
Apparatus includes
- Corkboard, sheets of conductive graph paper, pushpins
- DC multimeter & probes, power supply & wires, alligator clips
B. Setup conductive sheets
1. One lab partner should operate the DMM, another should record the position of the
equipotential points (as you find them). Make sure you record the location of the two
electrodes so you can reproduce them accurately on your graphs.
(a) Orient the conductive sheet with the Pasco lettering along the top. Note the (x , y )
coordinates are labeled and match the Data Sheets below.
(b) You will have to use “½ points” e.g, (2, 3.5) to record some of your equipotential
coordinates in order to improve accuracy because the conductive sheet “+” marks are
1.0 cm apart – note that the entire black sheet is conductive, not just the “+” marks.
2. A pair of electrodes have been defined by a pattern painted with conducting silver ink on
black high resistance paper. Record (copy or trace) the electrode patterns onto a piece of
graph paper. Make copies later for each lab partner.
3. Place one of the conductive sheets on the corkboard and affix via pushpins on each corner.
Connect each painted electrode to the power supply using a positive (+, red) or negative
(−,black) wire and a pushpin. Do not completely break the conducting path of the painted
electrode with a pushpin hole.
5
Connect the black (negative, common or “com”) terminal of the DMM to the negative
terminal on the power supply.
You will use the (red) probe connected to the other voltage terminal of the DMM to measure
voltage difference.
4. Have your lab TA check your set-up.
The DMM should be set to read DC Volts (function V). Set the power supply to 10 Volts
DC.
5. With the free (red) probe of the DMM, touch the positive electrode and record the
potential difference measured by the DMM ___________. Press firmly to make good
electrical contact; however, do not puncture or otherwise damage the paper (or the painted
electrode).
Touch the DMM probe to various points on the positive electrode shape—each point on the
electrode should be an equipotential—i.e., should read the same voltage; if the potential
seems to vary check that you have firm connections to the electrode and contact your lab TA
if you cannot correct the problem.
6. Touch the free probe of the DMM to the negative electrode and record the (nearly zero)
reading. (Again: this electrode should also be an equipotential).
7. Explore the area between the electrodes with the free probe. Recall that your DMM probe
is grounded at the negative electrode (reads zero voltage there), so the potential “differences”
you are reading on the DMM are the absolute voltage minus a zero voltage. Record your
voltage readings at roughly equal distances between the two electrodes and your
observations, which will be used to answer Question #1 below.
C. Find Equipotentials
8. Now select a point between the 2 electrode shapes, but closer to the negative electrode
where you get a reading of about1.0 volts and record the position of this point on the
included graph paper. Now, move the free probe (no more than ~ 1 cm) until you find
another point that reads about 1.0 volts. This second point is an equipotential with the first
point you found. Record the position, and draw a smooth line between the two points. (Note:
You need to make adjustments if the graph paper you are using has lines that are not spaced
at 1.0 cm).
Continue finding points that read 1.0  0.1 volts all along the front and sides of the
negative electrode.
6
9. Repeat step C.8 for voltage readings of 2.0-9.0 volts in 1 volt increments, giving you a
total of 9 equipotential lines between the two electrodes.
10. Repeat steps B. 3-7 and C. 8-9 for the other electrode conductive sheets provided by your
TA.
D. Draw E field lines
11. Working as a group with the graphed equipotential lines, determine how the E-field lines
should be drawn between the two electrodes, and draw in about 6 of them making sure you
follow the rules for E-field lines and the relationships with equipotential lines.
zero) reading. (Again: this electrode should also be an equipotential).
7. Explore the area between the electrodes with the free probe. Recall that your DMM probe
is grounded at the negative electrode (reads zero voltage there), so the potential “differences”
you are reading on the DMM are the absolute voltage minus a zero voltage. Record your
voltage readings at roughly equal distances between the two electrodes and your
observations, which will be used to answer Question #1 below.
C. Find Equipotentials
8. Now select a point between the 2 electrode shapes, but closer to the negative electrode
where you get a reading of about1.0 volts and record the position of this point on the
included graph paper. Now, move the free probe (no more then ~ 1 cm) until you find
another point that reads about 1.0 volts. This second point is an equipotential with the first
point you found. Record the position, and draw a smooth line between the two points. (Note:
You need to make adjustments if the graph paper you are using has lines that are not spaced
at 1.0 cm).
Continue finding points that read 1.0 +/- 0.1 volts all along the front and sides of the
negative electrode.
9. Repeat step C. 8. for voltage readings of 2.0 – 9.0 volts in 1 volt increments, giving you a
total of 9 equipotential lines between the two electrodes.
10. Repeat steps B. 3 – 7 and C. 8 – 9 for the other electrode conductive sheets provided by
your TA.
7
D. Draw E-field lines
11. Working as a group with the graphed equipotential lines, determine how the E-field lines
should be drawn between the two electrodes, and draw in about 6 of them making sure you
follow the rules for E-field lines and the relationships with equipotential lines.

Your data section should contain a description of the electrodes (including coordinate
locations for your graphs) for each sheet you measured; tables of your raw data coordinates and voltage readings

Your results should contain a graph of each electrode setup with equipotential (blue
color) and electric field lines (red color & determined from E field rules). Include the
charge on each electrode as well.
DATA TABLES
Electrode Shape #1: _____________________________
Eqpot #
1
2
3
4
5
6
7
8
9
Voltage (v)
Electrode Shape #2: _____________________________
Eqpot #
1
2
3
4
5
6
7
8
9
Voltage (v)
8
Electrode Shape #3: _____________________________
Eqpot #
1
2
3
4
5
6
7
8
9
Voltage (v)
TA Signature: __________________________________________
DATA GRAPH PAPER IS ON THE LAST 3 PAGES
3. Questions
1. Comment on what you observed when you measured the voltage potentials between
the positive and negative electrodes—where were the measurements the largest,
smallest and how did they change as you moved the probe from the positive to the
negative electrode? What did this tell you about the relative strength of the electric
field at these various points between the two electrodes?
2. Describe any symmetry you see in the equipotential lines. How is any symmetry
influenced by the shape of the electrodes? Describe the distances between each of
your equipotential lines—do they change at any points between the electrodes?
3. Describe the E-field lines between the two electrodes. At what angle do they
intersect with the electrodes, the equipotential lines?
4. Where would the E-field have the largest and smallest magnitudes—why ?
5. Describe two sources of error for this experiment. Write two suggestions for
improving this lab.
9
10
11
12