Download Conservation of Energy

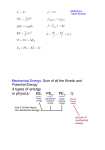
PHY 2053 Announcements
Sample exams and solutions
manuals for PHY2053 are
available at Target Copy
Two Kinds of Forces
Conservative and Non-Conservative
• A force is conservative if work done on object
moving between two points is independent of the
path the object takes between the points
– The work depends only upon the initial and final
positions of the object
– Any conservative force can have a potential energy
function associated with it
Examples of conservative forces include:
Gravity
(ideal) Spring force
Electromagnetic forces
• A force is nonconservative if the work it
does on an object depends on the path taken
by the object between its final and starting
points.
• Examples of nonconservative forces
– kinetic friction and air drag
•The blue path is shorter than the
red path
•The work required is less on the
blue path than on the red path
•Friction depends on the path and
so is a non-conservative force
Work-Kinetic Energy Theorem
• When work is done by a net force on an object and
the only change in the object is its speed, the work
done is equal to the change in the object’s kinetic
energy
Wnet = KEf − KEi = ∆KE
•
– Speed will increase if work is positive
– Speed will decrease if work is negative
Work and Potential Energy
Conservative force
potential energy function
Evaluating the difference of the function at any two
points in an object’s path gives the negative of the
work done by the force between those two points
Example will be gravity
Work and Gravitational Potential Energy
• PE = mgy
Wg ,on −book = mg ( yi − y f ) = mgyi − mgy f = PEi − PE f
Units of Potential Energy, Work, and
Kinetic Energy are same
joules
Work-Energy Theorem
Wnc = (KEf − KEi )
+(PEf − PEi ) =? 0
(if conservative)
Conservation of Energy
KEi + PEi = KE f + PE f
Reference Levels for Gravitational
Potential Energy
• A location where the gravitational potential energy
is zero must be chosen for each problem
– The choice is arbitrary since the change in the potential
energy is the important quantity
– Choose a convenient location for the zero reference
height
• Often the Earth’s surface
• May be some other point suggested by the problem
– Once the position is chosen, it must remain fixed for the
entire problem
Reference Levels, cont
• At location A, the desk
may be the convenient
reference level
• At location B, the floor
could be used
• At location C, the ground
would be the most logical
reference level
• The choice is arbitrary,
though
Problem Solving with Conservation of Energy
• Define the system- Verify only conservative forces do work
• Select the location of zero gravitational potential energy
Do not change this location while solving problem
• Identify two points the object of interest moves between
At one point information is given
At other point you want to find out something
• Apply the conservation of energy equation to the system
HITT RF Remote Login Procedure:
(If you have a really old IR remote you do not need to login.)
The radio channel number for this room is “07” (zero, seven).
It is STRONGLY recommended to login your remote for every class just
to be sure it is on the correct radio channel and working before class.
1.
2.
3.
4.
PRESS AND HOLD THE DOWN ARROW KEY until the
GREEN light on the remote turns RED.
PRESS THE “0” KEY and you will see the RED light flash
GREEN.
PRESS THE “7” KEY and you will see the RED light flash
GREEN.
PRESS AND RELEASE THE DOWN ARROW KEY again
and you will see the red light search for the receiver, if it
BLINKS GREEN MULTIPLE TIMES you are logged in.
In-class quiz 2/8
Your physics professor asks you to stand against the wall and
release a bowling ball hanging on a rope. As you let it go,
you want to jump out of the way, but your belief in what
physics law helps you repress this urge?
A.
B.
C.
D.
E.
Newton’s 1st Law
Law of Gravity
E=mc2
Conservation of Energy
Physics is Bogus
In-class quiz 2/8 (a)
A diver drops (does not jump) from a board 5 m above
the water. If he weights 700 N, what is his speed just
as he hits the water?
A. 700
m/s
B. 35 m/s
C. 14 m/s
D. 10 m/s
E. 0 m/s
v f = 2 gyi
In-class quiz 2/8 (b)
A diver drops (does not jump) from a board 10 m
above the water. If he weights 700 N, what is his
speed just as he hits the water?
A. 700
m/s
B. 35 m/s
C. 14 m/s
D. 10 m/s
E. 0 m/s
v f = 2 gyi
In-class quiz 2/8 (a)
Three different mass projectiles are launched from the
top of a building each at different angles of elevation.
Each particle has the same initial kinetic energy. Which
particle has the greatest speed just as it impacts with the
ground?
1. The one launched at the highest angle of
elevation.
2. The one with the highest mass.
3. The one with the lowest mass.
4. They all will have the same speed on impact.
5. Not enough information.
In-class quiz 2/8 (b)
Two blocks are released from the top of a
building. One falls straight down while the
other slides down a smooth ramp. If all friction
is ignored, which one is moving faster when it
reaches the bottom?
1.
2.
3.
4.
The block that went straight down.
The block that went down the ramp.
They both will have the same speed.
Insufficient information to work the problem.
A skier, starting from rest, slides down a 20° frictionless
slope to a flat area 20 m vertically below him. (a) Find
the skiers speed at the bottom. (b) How far does he slide
on the flat if the coefficient of friction between her skis
and the snow on the flat is 0.25?
In-class quiz 2/8
A skier, starting from rest, slides down a 20° frictionless
slope to a flat area 20 m vertically below him. How far
does he slide on the flat if the coefficient of friction
between her skis and the snow on the flat is 0.25?
A.
B.
C.
D.
E.
2.00 m
6.26 m
20.0 m
40.3 m
80.0 m
Spring Force
Hooke’s Law gives the force
F=-kx
k is spring constant
• F is the restoring force
• F is in the opposite direction of x
• k depends on how the spring was
formed, material from which it
was made, thickness of the wire,
etc.
Spring Work
F varies with x: F = - k x
W=F*x only good if F constant.
Approximate with series of steps
Work is sum of areas of rectangles
= area under curve.
Linear spring is simple
A = ½ B h W = ½ xmax Fmax
= ½ k x2
= work done on spring
Potential Energy in a Spring
1 2
PE s = kx
2
Elastic Potential Energy
– related to the work required to
compress spring from its
equilibrium position to some
final, arbitrary, position x
Work = Potential Energy
Initial and Final Kinetic Energies=0
Work with Spring + Gravity
• Wnc = (KEf – KEi) + (PEgf – PEgi) + (PEsf – PEsi)
– PEg is the gravitational potential energy
– PEs is the elastic potential energy associated with a
spring
– PE will now be used to denote the total potential energy
of the system
Conservation of Energy: Spring + Gravity
• The PE of the spring is added to both sides of the
conservation of energy equation
• The same problem-solving strategies apply
(KE + PE g + PE s )i = (KE + PE g + PE s )f
Spring + Gravity-Conservative System
(KE + PE g + PE s )i = (KE + PE g + PE s )f
– PEg is the gravitational potential energy
PE g = mgy
– PEs is the spring potential energy
1 2
PE s = kx
2