Download 5. EMInductionNC

..
..
..
..
..
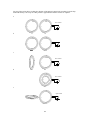
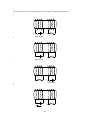
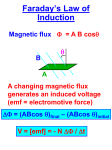
Electromagnetic Induction
Concepts and Principles
Creating Electrical Energy
When electric charges move, their electric fields vary. In the previous two chapters we
considered moving electric charges as the source of magnetic fields, but we could just as
easily have considered the variation in the electric field as the source of the magnetic field.
This leads to an interesting question: If varying electric fields can create magnetic fields, can
varying magnetic fields create electric fields? The answer is yes, and this process, termed
electromagnetic induction, is at the heart of almost all electrical power generation worldwide.
In addition to incredible technological importance, electromagnetic induction hints at a deep
inter-relationship and symmetry between electric and magnetic fields that will explored more
fully in later chapters.
Imagine a region of space with a magnetic field. Surrounding a portion of this region is a
hypothetical closed path. (Often, a real loop of wire will be the closed path of interest, but
induction occurs whether or not a real wire loop is present.)
B
First, let me define magnetic flux. The mathematical definition of magnetic flux is:
Φ = BA cosφ
where
B is the magnetic field within the area bounded by the closed path,
A is the area bounded by the closed path,
and φ is the angle between the magnetic field and the direction perpendicular to the
area. thus, if the field is perpendicular to the area, this angle is zero and the magnetic
flux is a maximum.
Conceptually, the magnetic flux is often visualized as the amount of field that “passes
through” the area enclosed by the path.
1
Second, let me define emf. (Actually, let me apologize. Emf used to stand for electromotive
force, even though it is not a force. In light of this misleading name, emf now, officially,
stands for emf. It’s not short for anything. I’m not making this up.) Emf is the name for the
electrical energy per unit charge created by changing magnetic flux. In general, any process
that generates electrical energy “creates” emf. In addition to changing magnetic flux,
chemical batteries and some solar cells create emf.
Mathematically, emf is defined as the product of the electric field that is created “around” the
closed path and the length of the path, although this definition is really all that useful in our
context. All you need to know is that emf is the energy created per unit charge. The units of
emf, joules per coulomb, are given the name volts (V). In crude language, an emf is a
“voltage”.
Let’s put this all together. The central relationship describing electromagnetic induction,
termed Faraday’s Law, claims that:
ε =−
∆Φ
∆t
where
ε is the emf induced (the voltage created) in the closed path,
Φ is the magnetic flux that passes through the closed path,
and the negative sign indicates that the emf’s direction in the closed path is to oppose
the change in magnetic flux. (If the closed path is a real loop of wire, the emf will
drive an induced current whose direction is such that the magnetic field produced by
this induced current is opposite to the change in magnetic field that produces the
induced current. Crystal clear?)
2
..
..
..
..
..
Electromagnetic Induction
Analysis Tools
Abrupt Change in Flux
A 100-turn, 1.0 cm radius coil of wire is 50 cm
from a very long straight wire carrying 2.0 A. If
the current flowing through the wire is turned
off, and drops to zero in about 0.1 s, what is the
average induced emf in the loop? What is the
direction of the induced current?
i
When the current is turned off, the magnetic flux through the small loop will decrease to zero.
By Faraday’s Law, this change in flux will create an emf in the loop. The first step toward
finding the emf involves finding the magnetic flux through the loop of interest. For this
example, the direction of the magnetic field is perpendicular to the loop’s area, so the angle in
the flux equation is 0°:
Φ = BA cos φ
Φ = BA
Moreover, since the loop is far from the wire, and the loop’s diameter is small, the magnetic
field from the wire is approximately constant over the area of the loop, and the initial flux is
given by:
Φ = BA
Φ initial = (
µ 0i
)( NπR 2 )
2πr
The N indicates the number of turns in the coil, each turn increasing the effective area of the
coil, r is the distance between the wire and the coil, and R is the radius of the coil.
Φ initial = (
(1.26 x10 −6 )(2)
)(100π (0.01) 2 )
2π (0.50)
Φ initial = 2.52 x10 −8 Tm 2
3
This flux is reduced to zero over 0.1s. Therefore:
ε =−
ε =−
∆Φ
∆t
(Φ f − Φ i )
∆t
(0 − 2.52 x10 −8 )
ε =−
0. 1
ε = 2.52 x10 −7 V
This is the average emf induced while the current decreases to zero. Although this is a small
value, it is easily measured by precision equipment.
Since initially the magnetic field through the loop was in the +z-direction, and was then
removed, the induced emf will drive an induced current counterclockwise around the loop in
an attempt to counter the reduction in flux. In other words, the induced current will try to
maintain a constant magnetic flux through the loop.
4
Continuous Change in Flux
A 1000-turn secondary coil of radius 2.0 cm is
concentric with a 400-turn primary coil of
radius 20 cm carrying AC current at 60 Hz with
peak current 2.0 A. What is the average emf in
the secondary coil as the AC current changes
from 2A clockwise to 2A counterclockwise?
i
current source
Again, the first step toward finding the emf involves finding the magnetic flux through the
secondary loop. For this example, the direction of the magnetic field is again perpendicular to
the loop’s area, so flux reduces:
Φ = BA
Moreover, since the magnetic field is approximately constant over the relatively small area of
the secondary loop, the flux is given by:
Φ = BA
N p µ 0i
2
Φ=(
)( N s πRs )
2R p
Plugging in values yields:
Φ=(
(400)(1.26 x10 −6 )(2)
)(1000π (0.02) 2 )
2(0.20)
Φ = 3.17 x10 −3 Tm 2
When the current flows clockwise, this flux is out of the page. When it flows
counterclockwise, the flux is into the page. Calling out of the page positive, and realizing that
the current changes direction in 120th of a second, results in:
ε =−
ε =−
∆Φ
∆t
(Φ f − Φ i )
∆t
((−3.17 x10 −3 ) − 3.17 x10 −3 )
ε =−
1
(
)
120
ε = 0.76V
Thus, as the primary current changes direction from clockwise to counterclockwise, the
secondary coil has an average induced “voltage” of 0.76V.
5
..
..
..
..
..
Electromagnetic Induction
Activities
6
For each of the actions below, indicate the direction of the induced current in the loop. The magnet and
loop center are in the same plane.
a.
S
N
v
b.
N
S
v
c.
S
N
v=0
d.
S
N
v
v
e.
S
N
v
7
For each of the actions below, indicate the direction of the induced current in the circular loop. The magnet
and loop center are in the same plane.
a.
S
N
v=0
b.
S
N
v
c.
S
v
N
d.
S
N
e.
N
8
S
For each of the actions below, indicate the direction of the induced current in the left loop. The loops are
parallel and their centers are coplanar.
a.
close switch
b.
open switch
c.
v
d.
open switch
e.
v
9
For each of the actions below, indicate the direction of the induced current in the left loop. The loops are
perpendicular and their centers are coplanar.
a.
close switch
b.
open switch
c.
close switch
d.
close switch
e.
v
10
For each of the actions below, indicate the direction of the induced current in the secondary loop (the loop
without the battery). The loops are either parallel or perpendicular and their centers are coplanar.
a.
close switch
b.
v
c.
close switch
d.
close switch
e.
open switch
11
For each of the actions below, indicate the direction of the induced current through the resistor.
a.
close switch
b.
open switch
c.
close switch
d.
v
12
The device below consists of a primary coil (containing an adjustable current source) and a secondary coil.
For the given primary current (ip) vs. time graph, construct the corresponding secondary current (is) vs. time
graph. Current to the right is considered positive.
i
current source
a.
ip
is
t
t
b.
ip
is
t
t
c.
ip
is
t
t
13
The device below consists of a primary coil (containing an adjustable current source) and a secondary coil.
For the given secondary current (is) vs. time graph, construct the corresponding primary current (ip) vs. time
graph. Current to the right is considered positive.
i
current source
a.
ip
is
t
t
b.
ip
is
t
t
c.
ip
is
t
t
14
The device below consists of a primary loop (containing an adjustable current source) and a secondary
loop. For the given primary current (ip) vs. time graph, construct the corresponding secondary magnetic
flux (φs) vs. time graph. Current to the right and flux out of the page are considered positive.
i
current source
a.
φs
ip
t
t
b.
φs
ip
t
t
c.
φs
ip
t
t
15
Six new prototypes for electrical generators are tested in the laboratory. Each generator consists of N
circular loops of wire with radius R rotated at frequency f in the same uniform magnetic field.
B
A
B
C
D
E
F
N
2000
1000
1000
4000
3000
500
R (cm)
10
10
20
5
10
20
f (Hz)
60
120
60
60
60
180
Rank these generators on the basis of the maximum emf produced.
Largest 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Smallest
_____ The ranking can not be determined based on the information provided.
Explain the reason for your ranking:
16
Six identical vertical metal bars start at the position shown and move at constant velocity through identical
magnetic fields. The bars make electrical contact with and move along frictionless metal rods attached to a
light bulb.
A
B
10 cm/s
10 cm/s
C
D
5 cm/s
20 cm/s
E
F
0 cm/s
10 cm/s
At the instant shown, rank these scenarios on the basis of the magnitude of the current in the light bulb.
Largest 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Smallest
_____ The ranking can not be determined based on the information provided.
Explain the reason for your ranking:
17
Six identical horizontal metal bars start at rest and fall vertically through identical magnitude magnetic
fields (except A). The bars make electrical contact with and move along frictionless metal rods attached to
a light bulb.
A
B
C
B
D
E
B
B
F
B
B
Rank these scenarios on the time it takes the horizontal bar to reach the bottom of the rods.
Largest 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Smallest
_____ The ranking can not be determined based on the information provided.
Explain the reason for your ranking:
18
Six identical horizontal metal bars start at rest and fall vertically through identical magnitude magnetic
fields (except A). The bars make electrical contact with and move along frictionless metal rods attached to
a battery.
A
B
C
B
D
E
F
B
B
B
B
Rank these scenarios on the time it takes the horizontal bar to reach the bottom of the rods.
Largest 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Smallest
_____ The ranking can not be determined based on the information provided.
Explain the reason for your ranking:
19
The 100 turn, 10 cm square loop at right is located in a 10 mT magnetic
field. The magnitude of the magnetic field is increased over a period of
0.50 s. The bulb's resistance is 30 Ω.
a. On the diagram above, indicate the direction of the induced current in the loop.
b. To what value should the field be increased in order to supply the 10 mA necessary to light the bulb?
Mathematical Analysis
20
B
The 5.0 cm square loop at right consists of 100 turns of wire and is located
in a 0.10 T magnetic field. The polarity of the magnetic field is reversed.
The bulb's resistance is 30 Ω.
a. On the diagram above, indicate the direction of the induced current in the loop.
b. Over what time interval must the reversal take place in order to supply the 10 mA necessary to light the
bulb?
Mathematical Analysis
21
B
A 200-turn loop of radius 1.0 cm is 50 cm from a very long straight wire
carrying 250 mA. The current is reduced linearly to zero in a time of 3.0 s.
i
a. On the diagram above, indicate the direction of the induced current in the loop.
b. What is the induced emf in the loop?
Mathematical Analysis
22
A 2000-turn secondary coil of radius 2.0 cm is concentric with a 200-turn
primary coil of radius 30 cm carrying current 300 mA. The primary
current is reduced to zero.
i
current source
a. On the diagram above, indicate the direction of the induced current in the loop.
b. Over what time interval must the primary current be reduced to zero to induce 6.0 V in the secondary
coil?
Mathematical Analysis
23
A coil of radius 2.0 cm is concentric with a 400-turn/cm solenoid carrying
current 1800 mA. The current is linearly reduced to zero over a time
interval of 0.05 s.
i
current source
a. On the diagram above, indicate the direction of the induced current in the loop.
b. How many turns are needed in the secondary coil to develop an emf of 12 V?
Mathematical Analysis
24
A 200-turn loop of radius 1.0 cm is 50 cm from a very long straight wire
carrying AC current at 60 Hz with peak current 250 mA. What is the
average induced emf in the loop as the current changes direction?
i
Mathematical Analysis
25
An n-turn secondary coil of radius r is concentric with a N-turn primary
coil of radius R. If the current source supplies AC current with maximum
current imax, what is the average induced emf in the secondary coil as the
current changes direction?
i
current source
Mathematical Analysis
26
A 1000-turn coil of radius 2.0 cm is concentric with a 400-turn/cm
solenoid carrying AC current at 60 Hz with peak current 2.0 A. What is
the average induced emf in the coil as the current changes direction?
i
current source
Mathematical Analysis
27
An N-turn coil of radius of R rotates at frequency f in a magnetic field B.
Determine the average induced emf each time the coil flips over.
Mathematical Analysis
28
B
A car alternator consists of a 250-turn coil of radius 5.0 cm. The coil
rotates at 1000 rpm in a 0.10 T magnetic field. Determine the average
induced emf each time the coil flips over.
Mathematical Analysis
29
B