* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Direction finding wikipedia , lookup
Nanofluidic circuitry wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Electronic engineering wikipedia , lookup
Oscilloscope history wikipedia , lookup
Topology (electrical circuits) wikipedia , lookup
Wien bridge oscillator wikipedia , lookup
Integrated circuit wikipedia , lookup
Phase-locked loop wikipedia , lookup
Flexible electronics wikipedia , lookup
Galvanometer wikipedia , lookup
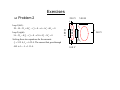
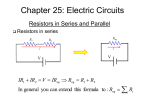
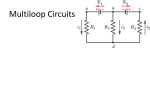
Chapter 25: Electric Circuits Resistors in Series and Parallel Resistors in series V V IR1 + IR2 = V = IReq ⇒ Req = R1 + R2 In general you can extend this formula to : Req = ∑i Ri Resistors in Series and Parallel Resistors in parallel V V 1 1 1 V V V = + ⇒ = + I = I1 + I 2 ⇒ Req R1 R2 Req R1 R2 I1 R2 V = I1 R1 = I 2 R2 ⇒ = I 2 R1 1 1 = ∑i In general you can extend this formula to : Req Ri Resistors in Series and Parallel Example 1: Resistors in Series and Parallel Example: (cont’d) I2 R2 I4 R4 I3 I R3 ∆V I = ∆V / Req = 12 V/2 Ω = 6 A I 3 = ∆V / R3 = 12 V/3 Ω = 4 A I 2 = I 4 = ∆V /( R2 + R3 ) = 12 V/(2 + 4 Ω) = 2 A Resistors in Series and Parallel Example: (cont’d) Kirchhoff’s Rules Introduction • Many practical resistor networks cannot be reduced to simple series-parallel combinations (see an example below). • Terminology: -A junction in a circuit is a point where three or more conductors meet. -A loop is any closed conducting path. junction Loop 2 i i i2 i1 i Loop 1 i2 i junction Kirchhoff’s Rules Kirchhoff’s junction rule • The algebraic sum of the currents into any junction is zero: ∑ I = 0 at any junction Kirchhoff’s Rules Kirchhoff’s loop rule • The algebraic sum of the potential differences in any loop, including those associated with emfs and those of resistive elements, must equal zero. ∑V = 0 for any loop Kirchhoff’s Rules Rules for Kirchhoff’s loop rule ∑ I = 0 at any junction ∑V = 0 for any loop Kirchhoff’s Rules Rules for Kirchhoff’s loop rule (cont’d) Kirchhoff’s Rules Solving problems using Kirchhoff’s rules Kirchhoff’s Rules Example 1 Kirchhoff’s Rules Example 1 (cont’d) Kirchhoff’s Rules Example 1 (cont’d) Kirchhoff’s Rules Find all the currents including directions. Example 2 Loop 2 i i i2 i1 i Loop 1 i2 i Loop 1 0 = +8V + 4V − 4V − 3i − 2i1 0 = 8 − 3i1 − 3i 2 − 2i1 0 = 8 − 5i1 − 3i 2 multiply by 2 i = i1+ i2 Loop 2 − 6i 2 + 4 + 2i1 = 0 − 6i 2 + 16 − 10i1 = 0 0 − 12 + 12i1 = 0 i1 = 1A − 6i2 + 4 + 2(1A) = 0 i 2 = 1A i = 2A Electrical Measuring Instruments Galvanometer To be discussed in a later class. Electrical Measuring Instruments Ammeter Electrical Measuring Instruments Ammeter (cont’d) Electrical Measuring Instruments Voltmeter R-C Circuits Charging a capacitor R-C Circuits Charging a capacitor (cont’d) R-C Circuits Charging a capacitor (cont’d) R-C Circuits Charging a capacitor (cont’d) R-C Circuits Charging a capacitor (cont’d) R-C Circuits Discharging a capacitor R-C Circuits Discharging a capacitor (cont’d) R-C Circuits Discharging a capacitor (cont’d) Exercises Problem 1 The resistance of a galvanometer coil is 25.0 Ω, and the current required for full-scale deflection is 500 µA. a) Show in a diagram how to convert the galvanometer to an ammeter reading 20.0 mA full scale, and compute the shunt resistance. b) Show how to convert the galvanometer to a voltmeter reading 500 mV full scale, and compute the series resistance. Solution a) For a 20-mA ammeter, the two resistance are in parallel: Vc=Vs->IcRc=IsRs->(500 x 10-6 A)(25.0 Ω) = (20 x 10-3 A – 500 x 10-6 A)Rs-> Rs=0.641 Ω. b) For a 500-mV voltmeter, the resistances are in series: Vab=I(Rc+Rs)->Rs=Vab/I – Rc -> Rs=500 x 10-3 V / 500 x 10-6 A – 25.0 Ω = 975 Ω. Rc=25.0 Ω 500 µA 20 mA Rs a) ammeter Rc=25.0 Ω Rs a Vab=500 mV b b) voltmeter 500 µA Exercises 36 − 5I 2 − 4( I 2 − I1 ) = 0 → 36 + 4 I1 − 9 I 2 = 0 Solving these two equations for the currents : I1 = 5.21 A, I 2 = 6.32 A. The current that goes through 4 Ω is I 2 − I1 = 1.11 A. 5.00 Ω I2 4.00 Ω loop 2 (right) : + I1 2.00 Ω loop 1 (left) : 20 − 14 − 2 I1 + 4( I 2 − I1 ) = 0 → 6 − 6 I1 + 4 I 2 = 0 20.0 V + v v + I1-I2 14.0 V v Problem 2 v 36.0 V Exercises 6.00 Ω V=18.0 V 6.00 µF b a S 3.00 Ω Problem 3 a) What is the potential of point a with respect to point b when the switch S is open? b) Which point, a or b, is at higher potential? Now the switch S is closed. b) What is the final potential of point b? c) How much charge flows through switch S when it is closed? Solution a) With an open switch: Q = CeqV = (2.00 × 10 −6 F)(18.0 V) = 3.60 × 10-5 C. Also, there is a current in the left branch: I = (18.0 V)/(6.00 Ω + 3.00 Ω) = 2.00 A. So V = V − V = Q / C − IR ab 6 µF 6Ω 6 µF 6 µF 3.00 µF = (3.6 × 10 −5 C)/(6.0 × 10-6 F) - (2.0 A)(6.0 Ω) = -6.00 V. b) Point b is at the higher potential. c) If the switch is closed: Vb = Va = (2.00 A)(3.00 Ω) = 6.00 V. d) New charges are: Q3 = CV = (3.00 ×10 −6 F)(6.0 V) = 1.80 ×10-5 C. Q6 = CV = (6.00 × 10 −6 F)(-12.0 V) = -7.20 × 10-5 C. → ∆Q3 = +3.60 × 10 −5 C - (1.80 × 10-5 C) = +1.80 × 10-5 C. ∆Q6 = −3.60 × 10 −5 C - (-7.20 ×10 -5 C) = +3.60 ×10 -5 C. The total charge flowing through the switch is 5.40 x 10-5 C.