* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download x + 1 - Postech
Intuitionistic type theory wikipedia , lookup
Lambda calculus wikipedia , lookup
Anonymous function wikipedia , lookup
Combinatory logic wikipedia , lookup
Falcon (programming language) wikipedia , lookup
Lambda lifting wikipedia , lookup
Lambda calculus definition wikipedia , lookup
Closure (computer programming) wikipedia , lookup
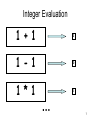
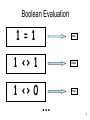
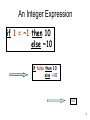
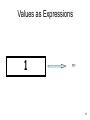
CSE-321 Programming Languages Introduction to Functional Programming 박성우 POSTECH March 8, 2006 Programming Paradigms • Structural programming – C, Pascal, … • Object-oriented programming – C++, Java, … • Logic programming – Prolog, … • Functional programming – SML, Haskell, Objective Caml, Lisp, Scheme, … 2 Outline • • • • • • • • • • Expressions and values Variables Functions Types Recursion Datatypes Pattern matching Higher-order functions Exceptions Modules 3 C • A program consists of commands. – command = “do something” • Nothing wrong: if (x == 1) then x = x + 1; else x = x - 1; • Nothing wrong either: if (x == 1) then x = x + 1; 4 SML • A program consists of expressions. – expression = “obtain a value” • Nothing wrong: if (x = 1) then x + 1 else x - 1 • But this does not make sense: if (x = 1) then x + 1 – what is the value if x <> 1? 5 Evaluation Expression Value • An expression “evaluates” to a value. • We “evaluate” an expression to obtain a value. 6 Integer Evaluation 1 + 1 2 1 - 1 0 1 * 1 1 … 7 Boolean Evaluation 1 = 1 true 1 <> 1 false 1 <> 0 true … 8 An Integer Expression if 1 = ~1 then 10 else ~10 if false then 10 else ~10 ~10 9 Values as Expressions 1 ??? 10 Everything is an Expression! if 1 = ~1 then 10 else ~10 • • • • • 1 ~1 1 = ~1 10 ~10 • if 1 = ~1 then 10 else ~10 11 Actually Not Everything if 1 = ~1 then 10 else ~10 • Ill-formed expressions – if 1 = ~1 then 10 (x) – if 1 = ~1 then 10 else ~10 (x) 12 Outline • • • • • • • • • • Expressions and values V Variables Functions Types Recursion Datatypes Pattern matching Higher-order functions Exceptions Modules 13 Variable Declaration - val x = 1 + 1; val x = 2 : int • A variable x is “bound” to value 2. • From now on, any occurrence of x is replaced by 2. - val y = x + x; val y = 4 : int 14 Local Declaration let val x = 1 val y = x + x val z = y + y in z + z end 8 15 Nested Local Declaration let let val x = 1 in val y = <expression> in x + x y + y end end let val y = let val x = 1 in x + x end in y + y end 16 Why “Local”? let val y = let val x = 1 in x + x end in x + y end okay??? 17 Variables are NOT variable. • The contents of a variable never change. • Surprise? – That’s because you are thinking about variables in imperative programming. variables in SML <> variables in C • Once you get used to functional programming, immutability of variables in functional programming will be taken for granted! 18 Then Why Variables? • Any advantage in using variables at all? let val x = 1 val y = x + x val z = y + y in z + z end VS. ((1 + 1) + (1 + 1)) + ((1 + 1) + (1 + 1)) What if it takes 10 hours to evaluate 1? 19 Outline • • • • • • • • • • Expressions and values V Variables V Functions Types Recursion Datatypes Pattern matching Higher-order functions Exceptions Modules 20 When is the first time you learned the concept of function? 21 즐거운 낱말 공부 시간 • 함수(函數): 두 변수 x, y간에 어떤 관계가 있어 x의 변화에 따라 y가 일정한 법칙으로 변화할 때 y를 x의 함수라 함. (function) (동아 마스타 국어사전) 22 즐거운 한자 공부 시간 •函 1. 함(함). 2. 편지(함) 3. 갑옷(함) 4. 넣을, 들일(함) 예: (書函) 서함: 책을 넣는 상자 23 Function = 函數 = Box Number! 24 Using a Box Number 25 Using a Box Number - Generalized … … 26 Function in SML = Box Number (fn x => x + 1) n = 27 Function Application … (fn x => x + 1) n • We “apply” (fn x => x + 1) to n. • x is called a formal argument/parameter. • n is called an actual argument/parameter. 28 Evaluating a Function Application … (fn x => x + 1) n n+ 1 … 29 Functions in SML • Nameless function – fn x => x + 1; • Storing a nameless function to a variable – val incr = fn x => x + 1; • Function declaration – fun incr x = x + 1; 30 Function Applications incr 1 (fn x => x + 1) 1 1 + 1 2 31 So far, So good, So easy. 32 First-class Objects • First-class objects = primitive objects – can be stored in a variable. – can be passed as an argument to a function. – can be returned as a return value of a function. • Examples: – integers – booleans – characters – floating-point numbers –… 33 First-class Objects in C • First-class objects – integers – characters – floating-point numbers – pointers – structures –… • Functions? – Function pointers are first-class objects. – But functions are not. • Why? You cannot create new functions on the fly! 34 Functions = First-class Objects in SML • Functions: – can be passed as an argument to a function. – can be returned as a return value of a function. 35 Box Number as Output … … such that … … 36 Box Number as Output x … … +x 37 Box Number as Output x y y+x 38 Box Number as Output x y fn y => y+x y+x 39 Box Number as Output x y fn y => y+x y+x fn y => y+x 40 Box Number as Output x y fn x => (fn y => y+x) fn y => y+x y+x fn y => y+x 41 In SML • Recall the following declarations are equivalent: – val incr = fn x => x + 1; – fun incr x = x + 1; • Then: – val add = fn x => (fn y => y + x); – fun add x = fn y => y + x; – fun add x y = y + x; • add takes only one argument, not two! • In fact, every function in SML takes only a single argument. 42 Adding Two Integers add 1 2 (fn x => (fn y => y + x)) 1 2 (fn y => y + 1) 2 2 + 1 3 43 Box Number as Input ( true, false) 44 Box Number as Input f fn f => (f true, f false) ( f true, f false) 45 Outline • • • • • • • • • • Expressions and values V Variables V Functions V Types Recursion Datatypes Pattern matching Higher-order functions Exceptions Modules 46 Types • A type specifies what kind of value a given expression evaluates to. – 1 + 1 : int – true andalso false : bool – #”A” : char – ”hello” : string – (1, true) : int * bool – (1, ~1, true) : int * int * bool – 1.0 : real – () : unit 47 Type Preservation Expression : T Value : T • An evaluation preserves the type of a given expression. • Type preservation will be discussed in detail later in this course. – It’s a lot more important than you might think! 48 Example let val x = 1 val y = x + x val z = y + y in z + z end : int 8 : int 49 Function Types • T -> T’ – type of functions: • taking arguments of type T • returning values of type T’ • Example: – val incr = fn x => x + 1; val incr = fn : int -> int – fun incr x = x + 1; val incr = fn : int -> int • Explicit type annotation – val incr = fn (x:int) => x + 1; val incr = fn (x:int) : int => x + 1; – fun incr (x:int) = x + 1; fun incr (x:int) : int = x + 1; 50 Type of add x fn x => (fn y => y+x) fn y => y+x 51 Type of add int fn x => (fn y => y+x) fn y => y+x 52 Type of add int fn x => (fn y => y+x) int -> int 53 Type of add int int -> (int -> int) int -> int 54 What is the Type? f fn f => (f true, f false) ( f true, f false) 55 f : bool -> int ? f : (bool -> int) -> fn f => (f true, f false) int * int ( f true, f false) 56 But why is it f : bool -> int ? 57 Why not f : bool -> char ? f : (bool -> char) -> fn f => (f true, f false) char * char ( f true, f false) 58 Then why not f : f : f : f : f : … bool bool bool bool bool -> -> -> -> -> string ? int * string ? unit ? (int -> int) ? <crazy type> ? 59 So we need Polymorphism. 60 Polymorph in Warcraft 2 • Cost: 2000 Gold Mana 200 Range: 10 Time to Upgrade: 200 Time Units. • • • • • • Perhaps the most fearsome of the Mage spells, Polymorph alters the physical form of its target. This metamorphosis changes man to beast, forever warping both mind and body. This sorcery wholly transforms the victim into a creature of the wolds, thus losing their reasoning - making commands for direction or battle impossible. This turns any living creature into the critter for that map type such as Pig for Wasteland, Seal for Snow, Sheep for Forest, Boar for Swamp. Although the unit hasn't been killed it has been in effect killed as it cannot be turned back into the previous unit or commanded in anyway. Polymorph is good for instantly taking out units, especially costly and dangerous units. The primary use for Polymorph is for hit and run attacks against enemy Mages, Death Knights, and Gryphons. Polymorph is really helpful on defense, especially on water maps. When the enemy lands you can quickly Polymorph the most dangerous enemy units right after they unload from the Transport. Make a Mage with at least 200 Mana Invisible, sneak up to an enemy Mage or Dragon and Polymorph it. If it is sea, do the pop out of the Transport Polymorph then run. Often you can cast Polymorph before the enemy even notices it, there is no warning to enemy players that their units have been Polymorphs. Against inattentive players you might be able to Polymorph quite a few units using hit and run attacks before they catch on. 61 Polymorphism in Warcraft 3 will be discussed in the next lecture. 62