* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download A v
Brownian motion wikipedia , lookup
Photoelectric effect wikipedia , lookup
Shear wave splitting wikipedia , lookup
Photon polarization wikipedia , lookup
Old quantum theory wikipedia , lookup
Centripetal force wikipedia , lookup
Seismometer wikipedia , lookup
Classical central-force problem wikipedia , lookup
Equations of motion wikipedia , lookup
Wave packet wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Hunting oscillation wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Matter wave wikipedia , lookup
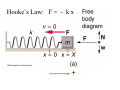
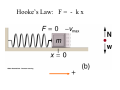
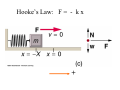
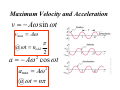
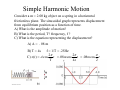
Chapter 13 • • • • • Hooke’s Law: F = - kx Periodic & Simple Harmonic Motion Springs & Pendula Waves Next Week! Superposition Review Physics 2A: Springs, Pendula & Circular Motion Elastic Systems F = −kx Small Vibrations Natural Frequency of Objects & Resonance All objects have a natural frequency of vibration or oscillation. Bells, tuning forks, bridges, swings and atoms all have a natural frequency that is related to their size, shape and composition. A system being driven at its natural frequency will resonate and produce maximum amplitude and energy. Coupled Oscillators Molecules, atoms and particles are modeled as coupled oscillators. Waves Transmit Energy through coupled oscillators. Forces are transmitted between the oscillators like springs Coupled oscillators make the medium. The Oscillation of Nothing Hooke’s Law Ut tensio, sic vis - as the extension, so is the force Hooke’s Law describes the elastic response to an applied force. Elasticity is the property of an object or material which causes it to be restored to its original shape after distortion. An elastic system displaced from equilibrium oscillates in a simple way about its equilibrium position with Simple Harmonic Motion. Robert Hooke (1635-1703) •Leading figure in Scientific Revolution •Contemporary and arch enemy of Newton •Hooke’s Law of elasticity •Worked in Physics, Biology, Meteorology, Paleontology •Devised compound microscope •Coined the term “cell” Hooke’s Law It takes twice as much force to stretch a spring twice as far. The linear dependence of displacement upon stretching force: Fapplied = kx Hooke’s Law Stress is directly proportional to strain. Fapplied ( stress ) = kx( strain) Hooke’s Law FRestoring = − kx •The applied force displaces the system a distance x. •The reaction force of the spring is called the “Restoring Force” and it is in the opposite direction to the displacement. An Ideal Spring Fspring = − kx An ideal spring obeys Hooke’s Law and exhibits Simple Harmonic Motion. Spring Constant k: Stiffness •The larger k, the stiffer the spring •Shorter springs are stiffer springs •k strength is inversely proportional to the number of coils Spring Question Each spring is identical with the same spring constant, k. Each box is displaced by the same amount and released. Which box, if either, experiences the greater net force? Hooke’s Law: F = - k x + Hooke’s Law: F = - k x + Hooke’s Law: F = - k x + Hooke’s Law: F = - k x + Hooke’s Law: F = - k x + Periodic Motion Position vs Time: Sinusoidal Motion SHM and Circular Motion x ( t ) = A cos θ ( t ) v(t ) = − Aω sin ω t a (t ) = − Aω 2 cos ω t 2π R v2 vt = Rω = , at = Rα , ac = = ω2R R Τ http://www.edumedia-sciences.com/en/a270-uniform-circular-motion Terms: Amplitude : [ A] = m Period : T = time / cycle, [T ] = sec 1 Frequency : f = (# cycles / sec), [ f ] = Hz Τ 2π Angular Frequency : ω = 2π f = , [ω ] = rad / s Τ Displacement of Mass Simple Harmonic Motion x ( t ) = A cos θ ( t ) 2π θ (t ) = ω t = t Τ Displacement of Mass Simple Harmonic Motion x ( t ) = A cos ω t v(t ) = − Aω sin ω t 2 a (t ) = − Aω cos ω t Displacement of Mass Notice: a = −ω x 2 2π ω= Τ Newton’s 2nd Law? x ( t ) = A cos ω t F = ma v(t ) = − Aω sin ω t 2 = m(−ω x) a (t ) = − Aω cos ω t 2 a = −ω 2 x = −kx k = mω k ω= m 2 angular frequency 2π ω= Τ Simple Harmonic Motion k ω= m Does the period depend on the displacement, x? T= 2π ω m T = 2π k The period depends only on how stiff the spring is and how much inertia there is. Finding The Spring Constant A 2.00 kg block is at rest at the end of a horizontal spring on a frictionless surface. The block is pulled out 20.0 cm and released. The block is measured to have a frequency of 4.00 hertz. a) What is the spring constant? 1 ω 1 f = = = Τ 2π 2π k m k = 4π 2 f 2 m 2 m k = 4π 2 (4 / s) 2 (2kg ) 2 = 1263 N / m m Harmonic Motion Described Frestoring = − kx m k T = 2π , ω= k m x(t ) = A cos ω t v(t ) = − Aω sin ω t 2 a (t ) = − Aω cos ω t Maximum Velocity and Acceleration v = − Aω sin ω t vmax = Aω @ω t = nodd π 2 a = − Aω cos ω t 2 amax = Aω @ ω t = nπ 2 Finding Maximum Velocity A 2.00 kg block is at rest at the end of a horizontal spring on a frictionless surface. The block is pulled out 20.0 cm and released. The block is measured to have a frequency of 4.00 hertz. a) What is the spring constant? b) What is the maximum velocity? k = 1263 N / m v(t ) = − Aω sin ω t vmax vmax = Aω 1263N / m = (.2m) 2kg k =A m = 5.0m / s Simple Harmonic Motion Consider a m = 2.00 kg object on a spring in a horizontal frictionless plane. The sinusoidal graph represents displacement from equilibrium position as a function of time. A) What is the amplitude of motion? B) What is the period, T? frequency, f ? C) What is the equation representing the displacement? A) A = . 08 m B) T = 4s f = 1/T = .25Hz 2π 2π π t = .08m cos t = .08m cos t C) x(t ) = A cos 2 4s Τ Simple Harmonic Motion Consider a m = 2.00 kg object on a spring in a horizontal plane. The sinusoidal graph represents displacement from equilibrium position as a function of time. x(t ) = .08m cos π t 2 D) What is the speed of the object at t = 1s? v = − Aω sin ω t vmax 2π 2π vmax = − Aω = − A = −.08m Τ 4s = −.13m / s E) What is the acceleration of the object at t = 1s? zero! Simple Harmonic Motion Consider a m = 2.00 kg object on a spring in a horizontal plane. The sinusoidal graph represents displacement from equilibrium position as a function of time. x(t ) = .08m cos π t 2 F) What is the spring constant? m T = 2π k 4π 2 m k= Τ2 k = 4.94 N / m 4π 2 (2kg ) = (4 s ) 2 SHM Question The position of a simple harmonic oscillator is given by ⎛π ⎞ x (t ) = (0.5 m) cos ⎜ t ⎟ ⎝3 ⎠ where t is in seconds. a) What is the period of this oscillator ? b) What is the maximum velocity of this oscillator? a) b) x(t ) = A cos ω t π 2π =ω = 3 Τ v(t ) = − Aω sin ω t vmax 2π = 0.5m 6s vmax = Aω = 0.52m / s Τ = 6s 2π =A Τ Energy in a Spring Mechanical Energy is Conserved! PEspring 1 2 = kA 2 KEspring 1 2 = mv 2 Energy in a Spring: Quiz Question What speed will a 25g ball be shot out of a toy gun if the spring (spring constant = 50.0N/m) compressed 0.15m? Ignore friction. Use Energy! PEspring = KEball 1 2 1 2 kx = mv 2 2 k v= x m Note: this is also =ωA = vmax 50.0 N / m v= (.15m) = 6.7 m / s .025kg Spring Question A 1.0-kg object is suspended from a spring with k = 16 N/m. The mass is pulled 0.25 m downward from its equilibrium position and allowed to oscillate. What is the maximum kinetic energy of the object? PEg = 0 Maximum kinetic energy happens at the equilibrium position. KEmax v(t ) = − Aω sin ω t 1 2 = mvmax 2 vmax = Aω 2 KEmax k =A m 1 ⎛ k ⎞ 1 2 1 2 = mvmax = m ⎜⎜ A ⎟⎟ = A k = 0.5J = PEm ax m⎠ 2 ⎝ 2 2 Simple Pendulum For small angles, simple pendulums exhibit Simple Harmonic Motion: Simple Pendulum For small angles, simple pendulums exhibit Simple Harmonic Motion: Restoring Force: F = −mg sin θ ≈ −mgθ θ = s/L F ≈ −mgs / L = −ks k = mg / L Amplitude : x = s For angles less than 15 degrees: ω = k m = mg / L m = g L ω= g L L T = 2π g Moon Clock At what rate will a pendulum clock run on the moon where gM = 1.6m/s2, in hours? Τ Earth L = 2π gE Τ Moon L = 2π gM Divide: ΤMoon = Τ Earth L 2π gM L 2π gE Τ Moon = Τ Earth gE = 2.45h gM • • • • result from periodic disturbance same period (frequency) as source Longitudinal or Transverse Waves Characterized by 1 f = Τ – amplitude (how far do the “bits” move from their equilibrium positions? Amplitude of MEDIUM) – period or frequency (how long does it take for each “bit” to go through one cycle?) – wavelength (over what distance does the cycle repeat in a freeze frame?) f – wave speed (how fast is the energy transferred?) v = λ Types of Waves Sound String Sound is a Longitudinal Wave Pulse Tuning Fork Guitar String Spherical Waves Wavelength and Frequency are Inversely related: f = The shorter the wavelength, the higher the frequency. The longer the wavelength, the lower the frequency. 3Hz 5Hz v λ Wave speed: Depends on Properties of the Medium: Temperature, Density, Elasticity, Tension, Relative Motion v=λf Speed of wave depends on properties of the MEDIUM v=λf Speed of particle in the Medium depends on SOURCE: SHM v(t ) = − Aω sin ω t Waves on Strings v=λf v= F μ (1D string) μ = m / L (linear mass density) Problem: v=λf The displacement of a vibrating string vs position along the string is shown. The wave speed is 10cm/s. A) What is the amplitude of the wave? B) What is the wavelength of the wave? C) What is the frequency of the wave? 4cm 6cm 1.67 Hz 10cm / s f = v/λ = = 1.67 Hz 6cm Problem: v=λf The displacement of a vibrating string vs position along the string is shown. The wave speed is 10cm/s. D) If the linear density of the string is .01kg/m, what is the tension of the string? Problem: F v= m/ L The displacement of a vibrating string vs position along the string is shown. The wave speed is 10cm/s. D) If the linear density of the string is .01kg/m, what is the tension of the string? F = v (m / L) 2 −5 F = (.1m) (.01kg / m) = 10 N 2 Problem: F v= m/ L The displacement of a vibrating string vs position along the string is shown. The wave speed is 10cm/s. e) If the the tension doubles, how does the wave speed change? Frequency? Wavelength? v2 = F2 2F = = 2v m/ L m/ L Wave speed increases by a factor of 2 Wave PULSE: • • • • traveling disturbance transfers energy and momentum no bulk motion of the medium comes in two flavors • LONGitudinal • TRANSverse Reflected PULSE: If the end is bound, the pulse undergoes an inversion upon reflection: “a 180 degree phase shift” If it is unbound, it is not shifted upon reflection. Free End Bound End Reflection of a Wave Pulse Reflection of a Traveling Wave Superposition Waves interfere temporarily. Pulsed Interference Standing Waves: Boundary Conditions Transverse Standing Wave Produced by the superposition of two identical waves moving in opposite directions. Standing Waves on a String Harmonics Standing Waves on a String λ1 = 2L λ2 = L 2L λ3 = 3 Standing Waves on a String 2L λn = n f n = v / λn v fn = n 2L Standing Waves on a String Harmonics The possible frequency and energy states of a wave on a string are quantized. v v f1 = = λ 2l v fn = n 2l f n = nf1 Strings & Atoms are Quantized The possible frequency and energy states of an electron in an atomic orbit or of a wave on a string are quantized. v f =n 2l En = nhf , n= 0,1,2,3,... h = 6.626 x10 −34 Js Multiple Harmonics can be present at the same time. Which harmonics (modes) are present on the string? The Fundamental and third harmonic. Standing Waves Standing waves form in certain MODES based on the length of the string or tube or the shape of drum or wire. Not all frequencies are permitted!