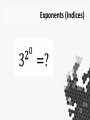* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Enhancing Your Subject Knowledge
History of trigonometry wikipedia , lookup
Approximations of π wikipedia , lookup
Wiles's proof of Fermat's Last Theorem wikipedia , lookup
Fundamental theorem of calculus wikipedia , lookup
Mathematical proof wikipedia , lookup
Fermat's Last Theorem wikipedia , lookup
Positional notation wikipedia , lookup
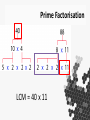
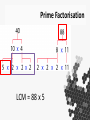
Enhancing Your Subject Knowledge #mathsconf8 Types of Subject Knowledge The Imperatives A* / 9 Teaching Experience Spotting Misconceptions Explanatory Making Sense Anecdotal Narrative Links Application The Imperatives • You should as a GCSE maths teacher be able to confidently solve the GCSE questions put in front of you. • e.g. “Find the nth term of this sequence: 3, 6, 11, 18, 27” Teaching Experience • “Find the nth term of this sequence: 3, 6, 11, 18, 27” • Likely errors: – Not halving the second difference – Only using the first two terms and creating an arithmetic nth term – Forgetting to find the second part of the nth term Basic Explanations But why does it work? • • • • Are we able to make maths make sense? Do we want it to make sense to students? Does it all make sense to us? You may be surprised at how little we interrogate the methods we use A whistle-stop tour… • • • • Some of this you may know Some may be new Some you may have simply forgotten Maybe you won’t see anything enlightening at all! Counting • • • • We have a base-10 number system The decimal system Decimal means ‘tenth’ Why do we have a base-10 number system? Counting • Does everyone count in base-10? • No • Papua New Guinea for example, has many different languages, and many different number systems! • Oksapmin is my favourite. • It has a base-27 number system Counting • 27 for 27 body parts • The words for each number are identical to the body parts OKSAPMIN Addition / Subtraction Algorithms • Our addition and subtraction algorithms are built around the decimal system, although they can be used for other bases with a little adjustment. “Carrying and Borrowing” • ‘Carrying’ is the exchange of a group of one unit to a unit of a higher power • e.g. ten units -> one ten Carrying • The process of carrying therefore is simply to ensure that the answer is in decimal format • How can we promote deeper understanding of the column method? -913 Different Bases • Try using the column method for these: (base 4) (base 5) Vocabulary Commutative Property • • • • 3+5+7=7+3+5=5+3+7=… 2 x 3 x 4 = 3 x 4 x 2 = 4 x 2 x 3 = ... Subtraction? Division? So what’s going on here? • 10 – 3 – 2 – 1 • 10 – 2 – 3 – 1 • 10 – 1 – 2 – 3 • 200 ÷ 2 ÷ 5 ÷ 10 • 200 ÷ 10 ÷ 2 ÷ 5 • 200 ÷ 2 ÷ 10 ÷ 5 Commutative? • Subtrahends are commutative • Divisors are commutative • Can help with mental maths: • 280 – 27 – 50 • 144 ÷ 36 ÷ 2 Why do these work? Is this more straight forward? Prime Factors, Factors and Multiples • List the factors of negative 20 Prime Factorisation Venn Diagram Prime Factorisation • • • • • • • • • Factors of 40? 1 2 4 (2 x 2) 5 8 (2 x 2 x 2) 10 (2 x 5) 20 (2 x 2 x 5) 40 (2 x 2 x 2 x 5) Prime Factorisation LCM = 40 x 11 Prime Factorisation LCM = 88 x 5 Finding Integer Roots Student Question Ideas 160 as a product of its prime factors is 25 x 5 Use this information to show that 160 has 12 factors ------------------2800 as a product of its prime factors is 2 4 x 52 x 7 How many square numbers are factors of 2800? Exponents (Indices) • When we stack exponents, we work right-toleft, so the answer is 3. • If we performed it left-to-right, we are essentially replicating (ab)c rather than creating something new. • Why does 3-1 = 1/3 ? • Why does 3 ½ = √3 ? • Why does 30 = 1? Embed these examples into your questioning • • • • • a 1 ÷ a1 = a 0 a0 ÷ a1 = a-1 1 ÷ a = a-1 a-1 ÷ a1 = a-2 1/a ÷ a = 1/a2 … and so on • a2 x a2 = a4 • a1/2 x a1/2 = a1 Geometry • Can you name these shapes? Ellipse • • • • An oval has no mathematical definition An oval is (literally) egg shaped Ovals often only have one line of symmetry Ellipses always have two. Square • • • • • • I of course mean parallelogram … I mean rectangle … I mean rhombus … I mean kite ... I mean trapezium All of the things. Rhombus • Diamonds are jewellery. • If we’re going to call them diamonds, we may as well call trapeziums ‘little tables’, and kites … kites. Stadium • Probably called a stadium because stadiums are shaped like it. • Strange how we don’t learn the name of this shape but it crops up in GCSE questions all the time! • Also called an obround and a discorectangle! Quadrilateral • This shape has 4 sides. • It is called a ‘crossed quadrilateral’ • A side is a straight line connection between two points. How many sides does a circle have? “the set of points equidistant from a fixed point” The Pythagorean Theorem • Try and prove it to yourself right now. • There are hundreds of different proofs for the Pythagorean Theorem. • We often rely on the ‘Bride’s Chair’ proof, but neglect to actually prove it! • The Bride’s Chair proof is actually one of the most complicated proofs of the Pythagorean Theorem. Slightly more straightforward proofs • By dissection PythagoreanProof Which of these is “The Pythagorean Proof”? Aryabhatta Trigonometry Tan(gent) Which of these cannot be a function? A function matches each x value with only one y value. Quadratic Sequences… • • • • 5, 13, 25, 41, … What is the nth term? Second difference is 4 2n2 + 3? Find the first 4 terms of this sequence: an2 + bn + c an2 + bn + c