Download What do the numbers 238, 235 written against the name of the

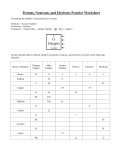
What do the numbers 238, 235 written against the name of the element uranium in the
preceding section mean? What elements are radioactive and what is meant by a
radioisotope? [This topic has much relevance as course material for students and hence is
covered in some depth to reiterate fundamental concepts. The coverage is in two parts.]
RADIOACTIVITY PART ONE: Basic Terminologies
By definition, each element has a unique atomic number (Z) representing the number of
protons in its nucleus. In a neutral atom the number of protons is equal to the number of
electrons, so that the atomic number also indicates the number of electrons.
Except for the atom of the most common form of hydrogen, which has one proton and one
electron, all atomic nuclei contain both the positively charged protons and the uncharged
neutrons. Protons and neutrons are called nucleons. The total number of these nucleons is
called the mass number (A). The number of neutrons in a nucleus of an atom of an element
can vary; this yields isotopes. Thus for uranium, we have the two common isotopes with
different mass numbers, 235 and 238, which can be written after the element’s name thus:
uranium-235 and uranium-238. The first isotope is used in nuclear reactors and atomic
bombs, whereas the second isotope lacks these properties.
The accepted way to denote the atomic number and mass number of an atom of element X
is as follows:
X.
Thus, for the element uranium, we can write
U to represent its
fissile isotope which makes up about 0.72% of natural uranium. There are three naturally
occurring isotopes of carbon on Earth: 99% of the carbon is carbon-12, 1% is carbon-13, and
carbon-14 occurs in trace amounts, i.e., making up as much as 1 part per
trillion (0.0000000001%) of the carbon in the atmosphere. The source of this isotope is the
interaction of neutrons in the incoming cosmic rays in the upper atmosphere with
atmospheric nitrogen which yields carbon-14 and a proton. These constantly replenished
carbon-14 atoms are soon oxidised by the atmospheric oxygen to become incorporated into
the molecules of atmospheric carbon dioxide. Since plants use atmospheric carbon dioxide
for their growth in photosynthesis, this radioactive carbon is incorporated into plants (and
the animals that eat them). This metabolic process only stops once a plant is cut down.
Since the half-life of carbon-14 is 5,730 ± 40 years, the decay will last for many millennia,
and by measuring the ratio of 14C to the ordinary 12C in old samples of wood, we are able to
estimate dates of origin. This is called carbon dating. By this method the age of carbonbearing materials up to about 58,000 to 62,000 years has been determined.
What is the force that holds the protons and neutrons together in the nucleus, overcoming
the electrostatic repulsion among the protons? It is the nuclear binding energy. The nuclear
binding energy is created from what is called mass defect. Let us see how this arises, taking
the case of the 16O atom, which consists of 8p and 8n in its nucleus, and 8 extra-nuclear
electrons. The mass of each of these separate particles is well-known and are, in amu
(atomic mass unit = 1/12th of the mass of the 12C isotope of carbon):
Mass of neutron = 1.00867 amu; mass of proton = 1.00728 amu; mass of electron =
0.00055 amu.
The sum of the masses of all the protons, neutrons and electrons in O 16 gives 16.13200 amu.
The mass of a 16O atom, however, is 15.99491 amu, relative to 12.00000 amu for 12C. This
leaves a discrepancy of 0.13709 amu which is released as energy as the nucleons bind
together. What this energy is can be computed using Einstein’s formula, E= Δmc2, where Δm
is the mass defect. The way to go about this calculation is often lost on students.
We begin by taking the mass of Avogadro’s number of 12C atoms as exactly 12 g.
Then, 1 amu = 1/12 x 12/Avogadro’s No. = 1/6.022x1023 = 1.660 x10-24 g. Using Einstein’s
formula, E=mc2, this gives 1.492 x10-10 J, and since 1eV = 1.602 x 10-19 J, we have 1 amu =
931 MeV.
For most nuclei, the average binding energy per nucleon is about 8 MeV. Consequently, this
amount of energy needs to be supplied to price a proton or neutron out of a nucleus.
Is there any connection between the nuclear binding energy and the strong nuclear force?
The strong force, due to gluon exchange between quarks, is of course what occurs within
protons and neutrons. The nuclear binding energy has been viewed by some as being
derived from this force due to “leakage” from gluon exchange resulting in an exchange of
pion (π-meson) particles between neutrons and protons.
If the repulsive forces between the protons outweigh attraction, the nucleus is unstable and
disintegrates, emitting particles and/or radiation. The principal factor for determining
whether a nucleus is stable is the neutron to proton ratio. For stable atoms of low Z, the
n/p value is close to 1. As Z increases, the n/p ratio increases to counteract the strong
repulsion among the protons. Generally, nuclei with even numbers of both protons and
neutrons are more stable than those with odd numbers of these particles. All isotopes of the
elements starting with polonium (Po, Z=84) are radioactive. All isotopes of technetium (Tc,
Z=43) and promethium (Pm, Z=61) are also radioactive. The advent of particle accelerators
has made possible the synthesis of elements with Z greater than 92. These are called
transuranium elements, the isotopes of which are all radioactive.
The detection of radiation from a radioactive nuclide can be realised based on four domains:
(1) ionization of a gas in an ionization chamber, a Geiger Muller tube or a cloud chamber; (2)
exposure of a photographic emulsion; (3) fluorescence of a phosphor as in a scintillation
counter; and (4) mobile charge-carriers in a semiconducting solid state detector.
Naturally occurring radioactivity results in the emission of three types of ionising radiation:
(1)
α- particles are positively charged (+2e) helium nuclei, He, which originate
from nuclei containing excess protons. All nuclei heavier than Pb (Z=82) exhibit
alpha activity.
X →
Y + He
(1)
Alpha-particles can be deflected by a magnetic or electric field. They have welldefined energies; typical speed is one-tenth speed of light. They are good
ionizers and lose their kinetic energy quickly.
(2)
β- particles are electrons ejected from nuclei having excess neutrons. They are
negatively charged (-1e) and possess a greater range and penetrating power
than α-particles, but have little ionizing ability. The radiation can be stopped by
a few mm of aluminium. β-particles emitted from a single radioactive isotope
show a wide energy spread, from almost zero to 0.9c. Since (as confirmed by αdecay) the energy liberation in a particular nuclear decay should be some
particular definite amount, it seemed that β-decay was violating the principle of
conservation of energy. However, it is now well established that along with βemission, there is an attendant emission of a sub-atomic particle called the
neutrino, a massless, neutral particle with half-integer spin that travels with the
speed of light and has its counterpart in the antiparticle. Since spin is in effect a
measure of angular momentum, it is clear that the ejection of a neutrino serves
to conserve both energy and momentum in the decay process.
(3)
Gamma (γ) radiation is not a mode of radioactive decay (such as α and β decay).
Rather, it is a mechanism by which a nucleus when transformed into a daughter
nucleus upon decay finds itself in an excited state and gets rid of its excess
energy through emission of electromagnetic radiation. (This is more frequent
than the alternate pathway, called internal conversion, where the excess
nuclear energy is passed on to one of the orbital electrons which then gets
ejected along with characteristic photons). Sometimes, though the excited
nuclear state of the daughter nucleus has a half-life that is more than 100 to
1000 times longer than the average 10-12 seconds, and this excited state is
referred to as a metastable nuclear excited state or nuclear isomer. The γ-ray
decay of this nuclear isomer is called isomeric transition. γ-rays have no rest
mass, carry no charge and travel with the speed of light. Unlike α- and βparticles, γ-rays are not affected by either electric or magnetic fields. γ-rays of
high energy can penetrate several cm of lead. They are more penetrating than
X-rays whose origins are external to the atom and associated with the
movement of electrons between energy levels.
This process of emission of particles and energy from an unstable nucleus of an atom to
form a stable product is called radioactive decay, and in the parlance of quantum
mechanics the term quantum tunnelling is used to describe how this phenomenon occurs.
A central dogma in quantum mechanics is wave-particle duality. One interpretation of this
duality involves the Heisenberg’s Uncertainty Principle (Δx.Δp > h/2π), which defines a limit
on how precisely the position and the momentum of a particle can be known at the same
time. There is a minimum for the product of the uncertainties of these two measurements.
There is likewise a minimum for the product of the uncertainties of the energy and time,
which is expressed by the relation ΔE.Δt > h/2π. The wave-particle duality was
mathematically first described by Schrodinger. His probability wave equation allows us to
discuss how a quantum particle encounters an energy barrier which is not infinitely thick
but whose height (U) is larger than the energy of the particle. Some of the amplitude of the
quantum particle is reflected, while some passes through the barrier (non-classical
behaviour), and emerges to continue travelling towards the right on the other side (Fig.1).
This possibility of particle detection on the other side of the barrier is known as quantum
tunnelling. Inside the barrier (region II), the Schrödinger wave equation will not have
oscillatory solutions, but exponential solutions. The interesting quantity to calculate is the
amount of transmitted wave amplitude relative to the incident amplitude. This is known as
the transmission coefficient which is the transmission or tunnelling probability.
Fig.1: A quantum particle tunnelling through a barrier
In the same way, the Heisenberg’s Uncertainty Principle explains why the alpha-particle
manages to escape from the nucleus. When the particle is originally very localised in space,
the level of uncertainty in its position is so small that it follows that the uncertainty of its
velocity becomes very large, possibly much greater than one would have expected, and
sufficient even to escape the pull of the nucleus. One might wonder why the unstable
nucleus does not simply emit the excess proton instead of the alpha-particle. Although rare,
this does happen with certain nuclei, but in the realm of probabilities, an alpha-particle
which has much larger mass and, therefore, greater kinetic energy, would need to ‘borrow’
less energy from its environment than would a proton with a similar large velocity
uncertainty to get over the energy barrier, and repay it within a certain time that does not
violate the Uncertainty Principle.
Reaction (1) leading to the release of alpha-particle is only possible if that particle suffers
tunnelling effect through the potential barrier created by the Coulomb repulsion between
the alpha particle and the rest of the positively charged nucleus. The alpha particle is not in
a bound state, otherwise, this decay could not occur. Moreover, alpha energy is positive and
its escape is only inhibited by the barrier presence. The tunnelling probability depends very
strongly on the height and width of the barrier and its shape (square or rectangular). Early
physicists pioneered by George Gamov were able to compute half-lives from tunnelling
probability calculations and find a theoretical relationship that explains not only the large
range of half-lives noted for alpha-decays but also the empirically discovered Geiger-Nuttal
Law. This law is commonly written in the form log10 t1/2 ≈ a - bZ/√Q, where t is in seconds, Z
is the atomic number of the daughter nucleus and Q, the energy of the emitted alphaparticle, is in MeV.
By way of example, the energy of the alpha particles emitted from 232Th is about 4 MeV
and its half-life is very long as 1.4 x 104 yrs. On the other hand, for 218Th the alpha particle
energy is about 10 MeV which is about 2.5 times larger than the case of 232Th and the halflife of 218Th is very short as 0.11 µ sec. The half-life is the time required for one-half of the
nuclei to undergo transitions.
One ordinarily measures a radioactive material by its disintegration rate rather than by the
number of atoms present. The curie (Ci) is defined as 3.7 x 10 10 disintegrations per second.
This definition implies widely differing number of atoms for one curie with different
radioisotopes. The SI unit is bequerel (Bq), which is defined as the amount of radioisotope
which gives one disintegration per second. Thus 1 Bq = 27 x 10-12 Ci.
For a given mass m (in grams) of an isotope with atomic mass ma (in g/mol), the amount of
radioactivity in Bq units can be calculated by first determining the total number of atoms
present that will undergo decay and next multiplying this by the decay constant (λ), which is
the probability per unit time (in sec) for one atom to decay. As will be discussed in PART
TWO, the decay constant is related to the half-life (t1/2 in sec) of the radioactive nucleus by
the equation, λ = ln 2/ t1/2.Thus, radioactivity (in Bq) = (m/ ma).NA. λ = (m/ ma).NA. (ln 2/ t1/2),
where NA is Avogadro’s constant.
vg kumar das (22 June 2012)
[email protected]