* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 6 - Rutgers Physics
Relativistic quantum mechanics wikipedia , lookup
Renormalization wikipedia , lookup
Chemical bond wikipedia , lookup
Molecular Hamiltonian wikipedia , lookup
Bremsstrahlung wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Matter wave wikipedia , lookup
James Franck wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Auger electron spectroscopy wikipedia , lookup
Elementary particle wikipedia , lookup
X-ray photoelectron spectroscopy wikipedia , lookup
Wave–particle duality wikipedia , lookup
X-ray fluorescence wikipedia , lookup
Geiger–Marsden experiment wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
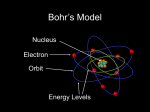
Tight binding wikipedia , lookup
Atomic orbital wikipedia , lookup
Electron configuration wikipedia , lookup
Honors Physics III Lecture 6: Bohr Model of the Atom http://www.physics.rutgers.edu/ugrad/273a Weida Wu Announcements First Midterm Oct. 5th 10-minute talk after Oct. 12’s class Review on Monday Oct. 3rd. Details to come soon on the course website Navy Nuclear Propulsion Officer programs Given by Naval Officer Recruiter Graduate Student Physics Tutors 2 Graduate Student Physics Tutors The physics graduate students in the list below have indicated an interest in tutoring students in undergraduate physics courses. If you would be interested in having a tutor for one of these courses, please feel free to contact them. The tutoring is for a fee that you will need to negotiate with the tutor. There is in addition free peer tutoring offered at the Rutgers Learning Centers https://rlc.rutgers.edu/studentinfo/group-and-individual-academicsupport/peer-tutoring http://physics.rutgers.edu/descr/tutorpage2016.pdf 3 Convenient units The electron’s rest energy E0=mc2 is =(9.11×10-31 kg)(3.0×108 m/s)2 ≈ 8.2×10-14 J It’s frequently more convenient to measure energy in units of electron volts: The amount of energy gained by a single electron when moved across an electric potential difference of one volt. Using 1 eV=1.6×10-19 J, so E0=0.511 MeV can write electron mass m=E0/c2 = 0.511 MeV/c2 This implies a new, useful unit of mass (MeV/c2) and momentum (MeV/c) Of course, we can also use eV/c, keV/c, GeV/c, etc... 4 Line Spectra Unlike continuous spectra from blackbodies, chemical elements produced discrete spectra. 19th century experiments would excite elements (by applying high voltage) and study their optical spectra. (Recall demo from Monday) Emitted light is passed through a diffraction grating with thousands of lines per ruling and diffracted according to its wavelength λ by the equation: where d is the distance of line separation and n is an integer called the order number. 5 Balmer Series In 1885, Johann Balmer found an empirical formula for wavelength of the visible hydrogen line spectra in nm: nm (where k = 3,4,5…) In fact, the Balmer series was only the first of several series to be discovered (first because it was the only series in the visible part of the light spectrum). 6 Rydberg Formula Johannes Rydberg and Walther Ritz found a more general empirical equation for calculating the wavelengths: RH=1.097×107 m-1 n and k are integers (where k>n) For each value of n, the set of wavelengths constitutes a “series” 7 In fact, what was being observed were transitions between different energy levels. The Lyman series was the transition to the lowest level (i.e. the ground state). 8 Atomic theory of matter First proposed by Greek philosophers Supporting evidence from physics and chemistry Evidence of substructure of atoms Atoms are building blocks of matter Discovery of electrons (J.J. Thomson, 1897) What is the structure of atoms? 9 Models of Atoms Atoms contain negatively charged electrons 2) Overall, atoms are electrically neutral 3) Electrons account for only a tiny fraction of an atom’s mass Thomson Model (1898): Uniform positive charge with embedded electrons 1) 10 Please try this at home: http://phet.colorado.edu/en/simulation/rutherford-scattering 11 Models of Atoms Geiger-Marsden Experiments (1911): Ernest Rutherford, with Hans Geiger and Ernest Marsden (a graduate student) scattered alpha particles from a radioactive source off of a thin gold foil. Measure scattering angles θ. Much larger deflections observed. Too many values of θ, even 180o! This was impossible in Thomson model. http://hyperphysics.phy-astr.gsu.edu/Hbase/hframe.html (Alpha-particle = 2 protons + 2 neutrons) 12 Rutherford Model “It was quite the most incredible event that has ever happened to me in my life. It was almost as incredible as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you. On consideration, I realized that this scattering backwards must be the result of a single collision, and when I made calculations I saw that it was impossible to get anything of that magnitude unless you took a system in which the greater part of the mass of the atom was concentrated in a minute nucleus. It was then that I had the idea of an atom with a minute massive center carrying a charge.” Lord Rutherford, 1936 13 Models of Atoms Rutherford Model (1915): Positive charge is contained in a tiny by massive nucleus. Electrons orbit the nucleus. Experiments agreed with Rutherford model. 14 Composition of Atoms If matter is primarily composed of atoms, what are atoms composed of? Michael Faraday (1833): Discovered the law of electrolysis J.J. Thomson (1897): Identification of cathode rays as electrons and measurement of ratio (e/m) of these particles Electron is a constituent of all matter! Humankind’s first glimpse into subatomic world! Robert Millikan (1909): Precise measurement of electric charge Mass ∝ (q)(atomic weight)/(valence #) Showed that particles ~1000 times less massive than the hydrogen atom exist Rutherford, with Geiger & Marsden (1910): Established the nuclear model of the atom Atom = compact positively charged nucleus surrounded by an orbiting electron cloud 15 The Hydrogen Atom Pre-Quantum era questions about the Hydrogen Atom Why does the Rydberg formula work? Why is the absorption spectrum the same as the emission spectrum? Why is the ionization energy of Hydrogen 13.6 eV? Why is the atom stable in the first place? 16 Classical Atomic Model Recall what would happen if we apply classical electromagnetism to an electron orbiting a proton. Coulomb’s Law binds electron to proton, but the electron is accelerating. An accelerating electron emits electromagnetic radiation (this is an unavoidable consequence of Maxwell’s equations). Eventually (10-9 seconds) the electron loses enough energy through radiation and collides with the nucleus (proton). 17 The Bohr Atom The idea of the nuclear atom (Rutherford’s planetary model) raised many questions at the next deeper level. How do the the electrons move around the nucleus and how does their motion account for the observed spectral lines? In 1913, Niels Bohr published a revolutionary three-part paper. 18 Bohr Model of Hydrogen Atom Assumptions: 1. Electron can only be in circular orbits that have orbital angular momenta: 2. 3. (n is the principal quantum number) Atom does not radiate while in such states Atom radiates when electron jumps from one allowed orbit to another. Emitted photon carries off difference in energy between the orbits. 19 Bohr Theory of Hydrogen Atom Circular Oribit - In Bohr model, Coulomb force still provides centripetal acceleration: But now, orbital angular momentum is quantized: Put lower equation into above equation … 20 So the n allowed radii are: Bohr radius Bohr radius gives the minimum radius of the hydrogen atom, i.e. the smallest radius of the atom, because it describes the radius of the ground state, or the most tightly bound state of the atom. We now have radii in terms of fundamental constants! And radii are quantized! e.g. r1=a0=0.053 nm, r2=4a0=0.211 nm, r3=9a0=0.475 nm 21 Electron Speed in Hydrogen Atom So, now let’s try to solve for the speed. Since: and Then speed is quantized, too. where α is the called the “fine-structure constant”. Notice that it is dimensionless. The fine-structure constant will show up in various places and has an important role in fundamental physics. 22 Energy in Hydrogen Atom Let’s solve for the energy. Since the velocity was not (quite) relativistic, we can perform a classical calculation. We can plug our previous expressions for the velocity and radius into this equation, as well. We now get a quantized energy. The ground state of the H atom is for n=1 23 So what does this mean? We now have electron energy in each orbit in terms of fundamental constants! The negative energy means that we must add energy to hydrogen to ionize it. Energy is not only quantized, but it has a ground state (n=1) below which the photon (emitted by the electron) cannot fall. So we have shown that the Hydrogen atom is stable and it’s ground state is the measured ionization energy. There are also excited states (n>1). 24 Hydrogen Line Spectrum: Bohr Model Let’s compare to the Rydberg equation. The energy of a photon when a Hydrogen atom deexcites from one state to the next is: Solving for the inverse wavelength, we get But RH=0.01096776 nm-1 That’s really close, but can we do even better? 25 Reduced-mass Correction In fact the electron and the nucleus Nucleus are revolve around a common mass CM (the nucleus is not infinitely massive, although, compared to the electron, it’s close). Electron Replace mass in the equation with the reduced mass: where M is the mass of the nucleus. For Hydrogen, µ=0.99456m Once you do that, you get precisely the Rydberg constant (M=Mproton). 26 Absorption of Light If photon wavelength satisfies Rydberg formula, an electron in orbit will absorb the photon and jump to a higher orbit Therefore, absorption spectrum = emission spectrum 27 To Summarize From three assumptions, we have recovered the full atomic spectrum of hydrogen! 28 The discovery of deuterium (Urey, 1932) Natural hydrogen is 1 part in 6000 deuterium (nucleus has one proton and one neutron, i.e. a deuteron). So the reduced mass of deuterium is a little bit different than regular hydrogen. The well known Balmer line (n=3 to n=2 transition) has wavelength 656.5 nm. But for deuterium, it is 656.3 nm! In natural hydrogen, the regular emissions lines are accompanied by very faint lines from deuterium! 29 The Hydrogen Atom Pre-Quantum era questions about the Hydrogen Atom Why does the Rydberg formula work? Why is the absorption the same as the emission spectrum? Why is the ionization energy of Hydrogen 13.6 eV? Why is the atom stable in the first place? Addressed by the Bohr model. But the Bohr model is just that: a model. Why should the angular momentum be quantized in the first place? The answer will come with quantum mechanics. 30 Bohr’s Atomic model explained … Explained the limited number of lines seen in the absorptions spectrum of Hydrogen compared to emission spectrum Emission of x-rays from atoms Chemical properties of atoms in terms of electron-shell model 31 Deficiencies of Bohr Theory Many of the energy levels in hydrogen are actually doublets, i.e. two levels closely spaced in energy (wavelength). Bohr theory cannot account for this. Quantization of angular momentum is just assumed, not explained or derived. Cannot explain spectra of complex atoms (with more electrons). Notions of fixed radii and speeds are inconsistent with uncertainty principle (more on this next week). Bohr theory is non-relativistic. Not too bad since v/c=1/137, but it means theory can’t be exactly right. 32 Atomic excitation by electrons Franck-Hertz experiment Quantized absorption of electron kinetic energy. 33 Please try this at home: http://phet.colorado.edu/en/simulation/hydrogen-atom 34 Question 1 In the Bohr model, we have: A electron in an Hydrogen atom drops from the n=6 state to the n=2 state. What is true about the relationship between E6 and E2? A. E6=E2/9 B. E6=E2/4 C. E6=E2 D. E6=4E2 E. E6=9E2 35 Question 1 In the Bohr model, we have: A electron in an Hydrogen atom drops from the n=6 state to the n=2 state. What is true about the relationship between E6 and E2? A. E6=E2/9 B. E6=E2/4 C. E6=E2 D. E6=4E2 E. E6=9E2 36 Example A hydrogen atom goes from the n=4 state to the ground state. Find the atom’s recoil speed. By momentum conservation, patom=12.75 eV/c Atom’s mass ≈ proton mass = 938 MeV/c2 So non-relativistic formula is acceptable…. 37 Atom’s kinetic energy for v=4m/s works out to K=1/2 mv2 = 8.7 x 10-8 eV So it was ok to ignore it in developing the Bohr model! 38 Question 2 A. B. C. D. Mimicking the experiment of Rutherford, Geiger and Marsden, you fire alpha particles of about 5 MeV into an unknown target and measure the scattering angle. Which of the following is likely to affect the scattering angle of the alpha particles coming off of the target? The temperature of the target. The number of electrons orbiting the nuclei of the target. The Coulomb force between the alpha particle and the electrons in the target. The Coulomb force between the alpha particle and the nuclei of the target. 39 Question 2 A. B. C. D. Mimicking the experiment of Rutherford, Geiger and Marsden, you fire alpha particles of about 5 MeV into an unknown target and measure the scattering angle. Which of the following is likely to affect the scattering angle of the alpha particles coming off of the target? The temperature of the target. The number of electrons orbiting the nuclei of the target. The Coulomb force between the alpha particle and the electrons in the target. The Coulomb force between the alpha particle and the nuclei of the target. The Coulomb force dominates in scattering experiments at lower energies, and within the Coulomb force only the massive, positive nucleus of the target interacting with the alpha particle determines the scattering angle. 40 A. B. C. D. Question 3 In attempting to describe the atom, Bohr made a set of general assumptions. Which of the following statements is NOT a result or closely aligned with those general assumptions (the assumptions might not be quantum mechanically correct)? The radius of a hydrogen atom can be calculated from a certain combination of fundamental constants. Electrons in the hydrogen atom transfer between quantized energy states and can exist nowhere else in the atom but in these energy states. The velocity of the electron around the nucleus is the same in all orbits, although the shape of the orbit changes with higher values of n, the principal quantum number Stationary states are states where the electron accelerates around the nucleus but does not emit electromagnetic radiation. 41 A. B. C. D. Question 3 In attempting to describe the atom, Bohr made a set of general assumptions. Which of the following statements is NOT a result or closely aligned with those general assumptions (the assumptions might not be quantum mechanically correct)? The radius of a hydrogen atom can be calculated from a certain combination of fundamental constants. Electrons in the hydrogen atom transfer between quantized energy states and can exist nowhere else in the atom but in these energy states. The velocity of the electron around the nucleus is the same in all orbits, although the shape of the orbit changes with higher values of n, the principal quantum number Stationary states are states where the electron accelerates around the nucleus but does not emit electromagnetic radiation. The velocity of the electron is not constant according to Bohr, but instead changes with changing principal quantum number. 42