Download Summarizing Ecological Data

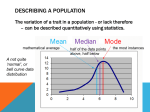
General Ecology (BIO 160)
Summarizing Ecological Data
Dr. Jim Baxter
Sacramento State
SUMMARIZING ECOLOGICAL DATA
Ecology has become an increasingly quantitative science. In part, this is because of the high degree of environmental variation that exists in ecological systems. As a science, ecology also seeks to make predictions about nature. Therefore, the study of ecology requires an understanding of basic quantitative methods. A foundation of this modern quantitative ecology is statistics. Statistics is an unbiased and quantitative way of making comparisons among different datasets or among different experimental treatments. Populations, Samples and Statistics Whenever we conduct an experiment, we wish to know whether or not our treatments had an effect or whether samples differ in some parameter of interest. When we collect data for such an experiment, we are actually collecting only a subset of the total possible data we could collect. The total possible data we could collect is called a population. The subset of data we actually collect is called a sample. Because our sample is only a subset of the entire statistical population of data, any descriptive values we might compute from such a sample are estimates of the true value for the entire population. Estimates based on samples are called statistics. In science, and especially in ecology, we are most often dealing with samples and hence must rely on statistics. Some examples of statistics are: mean, standard deviation, standard error, etc. The two most fundamental types of statistics used to describe a sample are: 1) measures of central tendency; and 2) measures of dispersion. Measures of Central Tendency Measures of central tendency are calculated values that simply describe the mathematical “center” of a sample or population. Mean The mean ( x ) is the most commonly used statistic and is often called the average. n
x + x 2 + x 3 + x 4 + ... x n
x= 1
n
or x=
∑x
i =1
n
i
where xn is an individual measurement, x i is the i th individual measurement, and n is the sample size (i.e., the number of measurements). An interesting property of the mean is that the sum of the deviations of all values from the mean is zero: n
∑ (x
i
− x ) = 0 i =1
This property will become important when we talk about measures of dispersion. Median and mode The median is the value that lies exactly in the middle of a distribution of observations when they are ranked in order from lowest to highest. In other words, 50% of the observations are higher and 50% of the observations are lower than the median value. The mode is the most frequently occurring value in a sample. 1
General Ecology (BIO 160)
Summarizing Ecological Data
Dr. Jim Baxter
Sacramento State
Measures of Dispersion These measures describe the spread of values around the measure of central tendency (usually the mean) for the sample or population. Range The range is the simplest measure of dispersion. It is the highest and lowest value of a set of observations. Yet, the range it is not the most useful measure of dispersion. For example: x x x x xxxxxx x xx x x x y y y y y y y y y y y y y y y y mean The above two sets of data have the same number of values, the same mean, and the same range. However, it is easy to see that the dispersion of data around the mean value is very different for each of these datasets. The ‘x’ dataset is clearly grouped more closely around a central mean value, while the ‘y’ dataset is spread more evenly. Variance The variance (s2) gets around the problem presented in the above example by taking account of the spread of the individual data points around the mean. Because the sum of the deviations around the mean equals zero – as indicated above – the variance uses the squared deviations around the mean. The equation for sample variance is: n
s2 = ∑ (x
− x)2
i
i =1
n −1
Because this equation is difficult to use, the variance is more easily calculated using the following formula: n
n
s2 = ∑x
∑ (x )
2
i
2
−
i
i =1
n
i =1
n −1
Standard deviation Because the variance is difficult to interpret, we typically use the standard deviation (s) as the measure of variation around a mean. A more conceptual definition of this statistic is given below. The standard deviation is simply the square root of the sample variance: n
n
s = ∑x
2
i
∑ (x )
2
i
−
i =1
i =1
n −1
n
Coefficient of variation The coefficient of variation (CV) is a relative measure of variation. The advantage of using the CV is that it can be compared across different samples that are derived from data that have very different magnitudes. Because the variance and standard deviation have values that are scales to the magnitude 2
General Ecology (BIO 160)
Summarizing Ecological Data
Dr. Jim Baxter
Sacramento State
of the data, these statistics cannot be used to directly compare the variation between samples that have data of different magnitudes (it’s like comparing apples and oranges!). For example, you may want to compare the variability of elephant’s ears to mouse’s ears. Because elephant ears are so much larger (~100 times larger) than mouse ears, the standard deviation of elephant ears will be ~100 times larger than that of mouse ears – even if they have the same relative degree of variation. The coefficient of variation solves this problem by expressing variation relative to the size of the sample mean. The CV is often expressed as a percent and is defined as: CV =
s
x
%CV =
or s
× 100 x
Frequency
The Normal Distribution Now that we understand measures of central tendency and dispersion, we must take the next step toward understanding statistical distributions. If we were to plot a frequency distribution of heights for all people in California, we would find that the distribution would fall out in a more or less symmetrical bell-­‐shaped curve, with most peoples’ heights being somewhere near the middle of the distribution and the heights of fewer people being at the higher or lower ends (tails) of the distribution. Many (but not all) ecological variables exhibit such a bell-­‐shaped curve. The theoretical distribution that describes this type of bell-­‐shaped curve is called a normal distribution. The normal distribution forms the underlying basis of many statistical tests and enables us to make statistical inferences about our data. A normal distribution is shown below: Normal distribution
1 SD
1.96 SD
x
Value
The normal distribution is defined by having a single central tendency, in which the mean, median and mode are equal. This distribution is also symmetrical, in that the right and left sides are mirror images of each other. In addition, the distribution has a characteristic amount of spread around the mean, which is defined by the standard deviation (s or SD). The larger the standard deviation, the wider the spread around the mean. The normal distribution also has the unique property that relates the standard deviation to probability values represented by areas under the curve. For example, for all normal distributions, 68.26% of the measurements lie within ±1 SD of the mean, 95% of the measurements lie within ±1.96 SD, and 99% of measurements lie within ± 2.58 SD. Thus, the normal distribution tells us something very important about the probability of measurements falling within certain areas of the distribution. This information will become useful when we statistically compare different means and determine the likelihood of significance for statistical tests. The Standard Error The standard error ( s x ), also written short-­‐hand as “SE”, is a statistic that tells us something about how precise our mean is as an estimate of the true population mean. A small SE tells us that our mean is 3
General Ecology (BIO 160)
Summarizing Ecological Data
Dr. Jim Baxter
Sacramento State
close to the true population mean, whereas a large SE tells us that our mean is likely to be far from the population mean. Remember that if we take a sample of a population and calculate the sample mean, this mean is only an estimate of the true population mean. The more samples we take – in other words the greater our sample size (n) – the more confident we will be that our mean is close to the true mean. Conceptually, the SE is a standard deviation of means. For example, if we were to go out and sample the same population again in exactly the same way, we would calculate a second mean that would likely be different from the first. If we took an infinite number of sample means in this way, we would find that they would tend to cluster around the true population mean (of course, this is a theoretical distribution; but this can be done on a computer). A frequency distribution of these sample means would itself produce a normal distribution, with its own mean and standard deviation. In this case, the expected mean of this distribution would be the true population mean. We can also calculate a standard deviation for this distribution. The standard deviation of this distribution of theoretical sample means is the standard error. The standard error s x is calculated as follows: s x = s
s2
= n
n
As stated above, s x is a standard deviation of means and therefore is also related to probability values. Given a normal curve, 68% of sample means would fall within ±1 SE of the mean, 95% would lie within ±1.96 SE, etc. Because the SE is a measure of how reliable an estimate our mean is, it is necessary to include this statistic together with any reported mean. A mean and its standard error should be expressed as: x ± SE. In interpreting the standard error, it is important to understand that the magnitude of s x is influenced by the sample size n and the standard deviation in the following ways: 1) The larger the sample size (n), the smaller the SE; and 2) The larger the standard deviation, the larger the SE. Confidence Intervals Any mean calculated from a sample is not likely to be exactly equal to the population mean. How different your calculated mean is versus the true population mean will depend on the size and variability of the sample. Confidence intervals (CI) are used to estimate the most likely range of values for the mean and include an upper and lower limit. They provide a quantitative measure of confidence in our estimate of the true population mean. Typically, we use 95% CI around the mean. What this means is that we can be 95% sure that the confidence interval includes the true population mean. To calculate 95% CI, we use the standard error and a value called the t-­‐value. Recall that the SE is a measure of how reliable our mean is and that it is dependent on the size and variability of the sample. That the SE reflects probability values just like the SD is also important and comes into play here. Because we typically collect fairly small numbers of samples (< 30), we cannot assume a normal curve and therefore cannot use 1.96 SE as the value that will give us 95% confidence. For this we rely on the t-­‐
value. The t-­‐value is determined from a probability distribution called the t-­‐distribution. The t-­‐
distribution is similar to the normal distribution but it is standardized to a mean of zero and its shape is affected by the sample size (degrees of freedom). At large sample sizes (>30), the t-­‐distribution approaches the normal distribution. For small sample sizes, it is wider and flatter than the normal distribution and has different probabilities associated with it. As used here, the t-­‐value is a multiplier 4
General Ecology (BIO 160)
Summarizing Ecological Data
Dr. Jim Baxter
Sacramento State
that scales the SE to the 95% level. To calculate the 95% confidence intervals for a mean, we use the following equation: s x . t-­‐value where s x is the standard error and t-­‐value is the value of t taken from a t-­‐table (available on the course website). To find the correct t-­‐value in the t-­‐table, you need to know the significance or alpha level (α) and the degrees of freedom (df). For this course, we will use α = 0.05 (more on this later). The degrees of freedom is calculated from the sample size (n) in our sample (see example below). The following is a sample calculation for 95% CI: Given the following information: n = 4, α = 0.05, x = 6, and s = 2.5 then, s x = s
n
= 2.5/2 = 1.25 and t(α, df) = t(0.05, 3) = 3.182 The value of t(0.05, 3) is determined by looking it up in the t-­‐table. At df = 3 and α = 0.05, t = 3.182 Therefore, the 95% confidence interval in this example is: 6 ± 1.25(3.182) 6 ± 3.98 To find the range, 6 + 3.98 = 9.98 6 – 3.98 = 2.02 Hence, we can be 95% sure that the true mean lies somewhere between 2.02 – 9.98 Suppose that instead of n = 4, we have n = 16: s x = s
n
= 2.5/4 = 0.625 Therefore: t(0.05, 15) = 2.132 6 ± 0.625(2.132) 6 ± 1.33 Hence, we can be 95% sure that the true mean lies somewhere between 4.67 – 7.33. Notice that the confidence interval narrows considerably as sample size increases. 5