Download Read Energy Conservation Handout

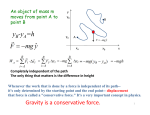
Considerations in Conservation of Energy Problems
Before discussing methods for conservation of energy problems, here are some fundamental concepts about work and
energy.
1.
Forces come in two general types as far as energy is concerned: conservative and non-conservative. The
textbook gives two definitions of conservative force. Review these as needed. For our purposes, the
conservative forces that we'll deal with the most this term are gravity and spring forces. In regard to spring
forces, it's important to realize that the Hooke's Law force (F = -kx) is the conservative one. It's possible for a
spring to obey a different force law that isn't conservative. The most common non-conservative force that
we'll deal with is friction.
2.
Potential energy is just a different way to deal with work. Potential energy is defined in terms of a change
and the work done by a conservative force. (Non-conservative forces don't have potential energy associated
with them.) If a conservative force does work, Wcons, on an object, the object's potential energy changes.
The work is the negative of the change in the potential energy: Wcons = Note that potential energy
doesn't have meaning except in terms of how it changes.
3.
Potential energy is always associated with a system. Therefore, when solving conservation of energy
problems, always specify the system. Consider, for example, an apple falling to the Earth. The gravitational
potential energy is a property of the apple-Earth system. (If you sometimes see mention of the gravitational
potential energy of a single object, keep in mind that this is simply a shorthand way of speaking about the
larger system.)
4.
Mechanical energy is a term that means the sum of the kinetic and potential energies of a system. All forms
of potential energy are included. For example, if an object is dropped onto a spring, the system includes the
object, the spring, and the Earth. There are 3 forms of mechanical energy to consider: kinetic energy of the
object, gravitational potential energy of the object-Earth system, and elastic potential energy of the spring.
5.
Mechanical energy is conserved when no non-conservative forces are present in the system. Energy can
change forms, but the total mechanical energy doesn't change with time. In the last example, the system
initially has only gravitational potential energy (Ug). As the object falls, some of the Ug is converted to KE.
As the object strikes and begins compressing the spring, both Ug and KE are being converted to elastic
potential energy (Ue). When the spring is compressed as far as possible, and the object is momentarily at
rest, all of the original gravitational potential energy has been converted to elastic potential energy.
6.
Conservation of mechanical energy for a system means that the mechanical energy of a system is the same
for all instants of time. In analyzing such systems, one selects two convenient instants, which are identified
as the initial and final states of the system. If, for example, one wanted to find how far the object of item 4
above compressed the spring, the initial state would be that of the object being released, and the final state
would be that of the spring being completely compressed.
Selecting a System for a Conservation Problem
Carrying out a conservation of energy analysis requires that you've specified the system. This is the most frequently
overlooked step in solving a conservation of energy problem. If you achieve a correct solution without specifying the
system, then you've really only stumbled onto the solution. This may work for simple problems, but you'll trip yourself
up on more complicated ones. Since you'll be doing the latter as well as the former, you may as well form good habits
now. So that means you need to specify the system. Let's see how.
Generally one selects for the system the objects that interact through conservative forces and cause potential
energy changes in the system. Mechanical energy (kinetic + potential) remains constant (is conserved) for
systems for which the only forces are conservative. Examples of conservative forces that we frequently
encounter are gravity and spring forces.
Example 1. Consider a ball that falls from rest in the absence of
air friction. Suppose your goal is to find the velocity of the ball
after it has fallen a certain distance. What are the interacting
objects? The answer is the ball and the Earth. They interact
through gravity, which is a conservative force. The Earth pulls on
the ball, and the ball pulls back on the Earth. So the system here
includes the ball and the Earth. Mechanical energy will remain
constant for this system, since the only force is a conservative
one.
system: ball, Earth (interacting through gravity)
Example 2. Suppose that the ball in the situation above is falling
in air. This means there will be a force of air friction. However, we
don't include the air in the system, because air friction is not a
conservative force. So the system is the same as that chosen for
Example 1. You may wonder how we know that air friction is a
non-conservative force. The test to apply is whether the total
work done over a closed path is 0. This means that there must be
as much negative work done as positive work so that the total
work is 0. This can never be the case for air friction. That's
because the force of air friction always opposes the motion of the
object; therefore, the work done by air friction is always negative.
Of course, the presence of air friction means that the ball
achieves a lower velocity than it would in falling the same
distance in a vacuum. This means that mechanical energy isn't
conserved. We'll see how to deal with this later when we solve
energy problems that include non-conservative forces.
system: ball, Earth (interacting through gravity)
Example 3. Here's another situation: A box slides down a
frictionless, inclined plane. Again, our goal is to find the speed of
the box after it has slid a particular distance. Interestingly, we
need only include the box and the Earth in the system. They
interact through the conservative force of gravity. Mechanical
energy is conserved for this system. You may wonder why the
plane isn't included, since it exerts a normal force on the box. The
answer is that the normal force can't change the energy of the
box. Work must be done on a system to change its energy. The
normal force can't do work, because it's always perpendicular to
the displacement of the object. (Note that if there is friction with
the plane, one still excludes the plane from the system, because-as we saw in Example 2--the friction force is non-conservative. In
that case, mechanical energy is not conserved.)
system: box, Earth (interacting through gravity)
A Problem for You. Consider a bob swinging in a pendulum
motion at the end of a string and in the absence of friction. The
goal is to find the speed of the bob after it has swung through a
particular arc. What would you pick for the system and why?
Would you include the string which exerts tension force on the
bob? Would mechanical energy be conserved?
Example 4. One more situation: A block oscillates horizontally
across a frictionless surface under the action of a spring.
Knowing the block's maximum displacement from the equilibrium
position, the goal is to find the speed of the block as it passes
through the equilibrium position. What would you pick for the
system? The spring force is conservative, so the block and the
spring would be included in the system. We don't need to pick the
Earth this time, because gravity doesn't change the energy of the
block. We don't need to pick the plane, because the normal force
can't change the energy of the block either.
system: block, spring (interacting through the spring force)