Download Lecture 21: Elastic Collisions and Conservative Forces

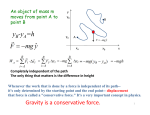
Lecture 21: Elastic Collisions and
Conservative Forces
• Another elastic collision example:
• We drop a tennis ball and a basketball from a height h.
The tennis ball is slightly above the basketball. What will
be the initial upward velocity of the tennis ball, assuming
all collisions are elastic?
• We begin by considering the motion of the basketball. Just
before hitting the ground, it has a velocity of v = − 2 gh
(we can obtain this result using the work-energy theorem)
• The collision between the ball and the earth is elastic, so:
mB vB ,i = mB vB , f + mE vE , f
vE , f =
mB ( vB ,i − vB , f
)
mE
1
1
1
2
2
mB vB ,i = mB vB , f + mE vE2 , f
2
2
2
mB ( vB ,i − vB , f
1
1
1
2
2
mB vB ,i = mB vB , f + mE
mE
2
2
2
v
2
B ,i
−v
2
B, f
mB
=
vB ,i − vB , f
(
mE
)
2
)
2
(v
(v
B ,i
B ,i
vB ,i
− vB , f
)( v
+ vB , f
mB
) = m ( vB,i − vB, f
E
B ,i
mB
+ vB , f ) =
vB ,i − vB , f
(
mE
)
2
)
mB
mB
1−
= −vB , f 1 +
mE
mE
vB , f = − vB ,i
mB
1−
mE
mB
1+
mE
• Since the earth is so much more massive than the ball, we
can approximate this as:
vB , f = − vB ,i = 2 gh
• Now for the tennis ball colliding with the basketball. Let’s
analyze this is the frame where the basketball is at rest. In
that case, we already know the answer:
vT , f = − vT ,i
mT
1−
mB
1+
0.057kg
0.55kg
= −0.81vT ,i
0.057kg
1+
0.55kg
1−
= − vT ,i
mT
mB
• In the frame where the basketball is at rest the initial
velocity of the tennis ball is
vT ,i = vTE ,i + vEB ,i = − 2 gh − 2 gh = −2 2 gh
• So the final velocity is:
vT , f = 1.62 2 gh
• Translating this to the frame of reference of the Earth, we
find:
vTE , f = vTB , f + vBE , f = 1.62 2 gh + 2 gh = 2.62 2 gh
• The tennis ball can reach a height almost 7 times greater
than that from which it was dropped!
Conservative Forces
• Consider the work done by gravity as an object is lifted a
height h and then lowered back to its original position
• On the upward trip, the work is mgh, while on the
downward trip it is –mgh
– Thus the total work done by gravity during the round trip is
zero
• Any force for which this is true (the work done by the
force during a round-trip is zero) is called a conservative
force
•
•
Another example: Force due to a spring
Imagine an object attached to a spring, which is then stretched
to a length x = d
1. The object will experience a force pulling it back toward x = 0.
The work done by the spring is
1 2
2
kd
2. The object shoots past x = 0, compressing the spring to x = -d.
The work done by the spring is
1 2
− kd
2
3. The object is now accelerated back toward x = 0. The work done
1 2
by the spring is
2
kd
4. The object once again shoots past x = 0, coming to rest when the
spring is stretched to x = d. The work done by the spring is 1
•
− kd 2
2
We see that the “round-trip” work is zero, so the spring force is
conservative
• Finally, consider friction
• An object slides down a ramp, experiencing friction as it
goes
– Since friction acts in the direction opposite the motion, it
does negative work
• Now the object is pushed back up the ramp by some other
force, but still experiences friction
– Once again, the work done by friction is negative (kinetic
friction always acts in the direction opposite the motion)
• The total work done by friction in the round-trip is not zero
• Friction is not a conservative force
Conservative Forces: Definition 2
• Consider an object moving from point 1 to point 2. Some
possible paths for the object are shown:
b
2
a
1
• In general, the complex motion that causes the object to
follow any one of these paths might be the result of several
forces acting on it
• But let’s consider one force, that happens to be
conservative
• The work done by the conservative force in following path
a from 1 to 2, then path b from 2 back to 1 must be zero:
2
Wtot =
F ( r ) ⋅ dr +
1,a
2
1,a
1
F ( r ) ⋅ dr = 0
2,b
1
2
2,b
1,b
F ( r ) ⋅ dr = − F ( r ) ⋅ dr =
F ( r ) ⋅ dr
• Therefore, the work done by our conservative force as the
object moves from 1 to 2 is independent of the path taken
• This property also can be used to define a conservative
force
Potential Energy
• We have already studied the work-energy theorem, which
relates the total work done on an object to the change in
kinetic energy:
Wtot = ∆KE
• For a conservative force, the work done by that force as an
object travels from point 1 to point 2 is defined. We define
a new kind of energy, potential energy, as:
WF = −∆U = U1 − U 2
– Note that here we are talking about the work done by a
single force
One-dimensional Case
• In general,
rf
∆U = U ( rf ) − U ( ri ) = −W = − F ⋅ dr
ri
– Note that only a difference in potential energy is meaningful,
since we can always redefine what we call r = 0
• If the force only acts in one dimension, and only depends
on one dimension, (call it x), this simplifies to:
xf
U ( x f ) − U ( xi ) = − Fx ( x ) dx
xi