Download Polynomials Factoring (A-5)

Polynomials & Factoring (A-5)
Polynomial: the most common type of algebraic expression.
Monomial: an algebraic expression consisting of a single term.
Binomial: an algebraic expression that has two terms.
Trinomial:. an algebraic expression that has three terms.
Common factor: a whole number that is a factor of each number in a set of numbers.
Factor: a number or expression that is multiplied by another to yield a product.
Remember that factoring is just "un-doing" multiplication.
Take the number 6, for example. We can write it as factors like this: (2)(3).
It works the same way with polynomials, but we have to consider our variables and GCF.
Greatest common factor (GCE):the greatest number that is a factor of two or more numbers
Identify the GCF(greatest common factor) in each expression.
1.4x+2y
2. 8x2 +9x
x
Quadratic equation: a polynomial equation of the second degree, generally expressed as ax2
c·= 0, where a, band c are real numbers and a is not equal to zero.
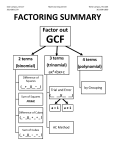
Types of Factoring to consider:
Take out GCF(check this first every time you factor)
Difference of squares
Sum & difference of cubes
Perfect square trinomial
Trinomial with leading coefficient of 1
Trinomial with leading coefficient NOT 1
Grouping
ALWAYS FIRST: look for a GCFin all terms. If there is one, factor out the GCFin front The
parentheses should contain the "left over" numbers after taking out the GCF.
Example: 15xy2 - 10 x3y + 25 xy3
Factored completely as 5xy( 3y - 2X2+ 5y2)
+ bx +
IF THERE ARE 2 TERMS: it could be .....
Difference of perfect squares:
Your answer is the product of two binomials. Take the square root of each term. One binomial
will have a positive sign between the terms and the other binomial will have a negative
between the terms.
Example: 4X2- 2Sy4 factors to (2x + Sy2)(2x - Sy2)
Sum or Difference of a perfect cube:
Your answer is a binomial times a trinomial. Binomial part is the cube root of each original
term with the same sign. For the Trinomial part only look at the new binomial (not the original
problem and use SOFAS). Square the first term, Opposite sign, multiply the first term by the
second term, Always positive, Square the second term.
Example: 8x3 - y3 factors to (2x - y)(4X2+ 2xy + y2)
IF THERE ARE 3 TERMS: it could be .....
Perfect square trinomial:
If the first and last term are perfect squares and the middle term is twice the product of the"
square root of the first and last.
Example: X2+ 6x + 9 factors to (x+3)(x+3) which can be written as (x + 3)2
Trinomial with leading coefficient of 1:
You must find two numbers that multiply to equal the last term and add to equal the middle
term, Your answer is the product of two binomials.
Example: "x2 - 4x - 12 find numbers that multiply to -12 and add to -4. The numbers are-6
and + 2, so the final factors are (x + 2)(x - 6)
Trinomial with leading coefficient not equal to 1:
Your answer will be the product of two binomials. There are a few different methods that
teachers often use. "The Magic Box","T-chart", guess and check. I will do the divide, reduce
and swing method here.
Example: 3x2 + lOx + 8
Swing the 3 to multiply to the 8 in order to obtain x2 + lOx + 24
Two numbers that multiply to be 24 and add to be 10 are 6 and 4, so we get the factors
(x+6)(x+4)
Now you must divide each constant by the 3 that was multiplied to the constant in the
6
4
3
3
first step to get (x + - )(x + -)
If possible, reduce all fractions to get
ex + 2) ex + ~)
3
Now, swing all denominators (that are not one) in front of the variable within the factor
to get (3x + 4) (x + 2).
IF THERE ARE 4 TERMS:
Grouping.
Group two terms together and another two terms together leaving an addition sign in between
the two binomials. Take out a GCF from each binomial. Your goal is that inside the parentheses
are identical. If this happens then you rewrite your answer as the product of two binomials.
Example: 12ac + 21ad + 8bc +14bd
Step 1.
(12ac + 21ad) + (8bc + 14bd)
Step 2.
3a(4c + 7d) + 2b(4c + 7d)
Step 3.
(3a + 2b)(4c + 7d)
Here are some more examples:
16m2n + 12mn2
GCF
\...
X
GCF
~
(X -2-)
~ff. of squares
Diff. of squares
(X +5) (X - 5)
()<'Z t l)
()<"2-_ l) -7 ~
[(X"-tIJ{xtl)(J(-I)
GCF! diff. of squares
v,
x3 + 125
)
> 3 (a -C1b?\? (tA 1- 3 b)[iA-3bJ\
Sum of cubes (!. + 5) ( x-z. - 5X +~5)
Z
~
Diff. of cubes
(0.. -
Sumofcubes
('/.
'3- (
'1.-
LIZ
l-,~\
b) (} +- tl0 + () )
+3jCX
'l-
-8X -I- q )
~
I
x2
+ 8x + 16
2b3
+ 32b2 + 128b
(y.. -t- Lf)(x -+- 4 )
Perfect Square Trinomial
GCF & trinomial
~
b( b2. 1- 1(.0 l? +
I? h [b + ~Xb
4w2
12wr + 9r2
-
-r~
(0 If)
)J ~
.?b [I?MlY
Perfect square trinomial
(?W - Br)(?vI - ~r)
(z X + Y) (L/ xz..- '2 xy +- y 2. )
Sum of perfect cubes
20x2
-
60x - 35
GCF & Trinomial
5"
(IL
'Z
'"T)<-J2X-I
t; 1)( t I )('2)( -I )
200 + 17r - r2
Trinomial
(~ +
6x2 + lOx - 4
rf?5 -
GCF & Trinomial
r)
\
,2 (~X~1- 5X -P)
\"1- (3)(
4x2
21-
+
8x - 4xy - 8y
xy - 7y + 3x
fR0n:x"p!
GCF & Grouping
Grouping
~)CPI-'f.y-7y
- I)(x -t 1.)\
L/)('" ti1tl/xy -ll0
..
4x(x +~) -4Y Cx-t-z.)
(?c f 2j (4 '1-lJy) -> tEn)(lC- Y)
(
ill.
->
3(x+-')-Y (X·FI) -? K>C-I-I)[3:"Y))