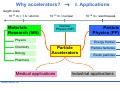
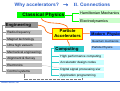
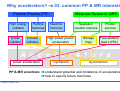
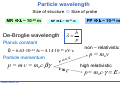
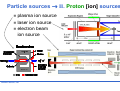
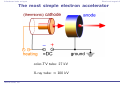
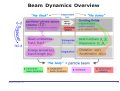
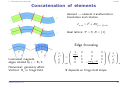
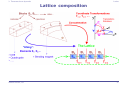
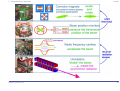
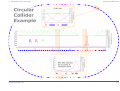
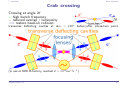
* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Particle Accelerators - Institute of Particle and Nuclear Physics
Aharonov–Bohm effect wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
Nuclear physics wikipedia , lookup
Thomas Young (scientist) wikipedia , lookup
Time in physics wikipedia , lookup
Standard Model wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Elementary particle wikipedia , lookup
History of subatomic physics wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Experimental Methods of Particle Physics Particle Accelerators Andreas Streun, PSI [email protected] http://people.web.psi.ch/streun/empp Andreas Streun, PSI 1 Particle Accelerators 1. 2. 3. 4. 5. 6. 7. 8. Andreas Streun, PSI Introduction Accelerator basics and types Transverse beam dynamics Longitudinal beam dynamics Emittance Synchrotron radiation Luminosity Muons and neutrinos 2 1. Introduction Books & webs Why accelerators? Particles Particles of interest Particle wavelength and momentum Particles to accelerate Particle production A beam of particles Beam quality Accelerator peformance Particle Physics experiments Center-of-mass energy Luminosity Andreas Streun, PSI 3 Books & Webs K. Wille, Physik der Teilchenbeschleuniger und Synchrotronstrahlungsquellen, Teubner Studienbücher, Stuttgart 1992. K. Wille, The physics of particle accelerators, Oxford university press, 2005. S. Y. Lee, Accelerator Physics, World Scientific, Singapore 1999 H. Wiedemann, Particle Accelerator Physics I+II, Springer, Berlin Heidelberg New York 2007. Proceedings of The CERN Accelerator School http://cas.werb.cern.ch/cas/ A. W. Chao and M.Tigner, Handbook of Accelerator Physics and Engineering, World Scientific, Singapore 1998. Proceedings of the Accelerator Conferences http://www.jacow.org/ Andreas Streun, PSI 4 Why accelerators? → I. Applications length scale 10-10 m = 1 Å / atomic 10-15 m / nuclear Nuclear Physics (NP) Materials Research (MR) Physics Chemistry Biology 10-18 m / electroweak Particle Physics (PP) Energy frontier Particle Accelerators Particle factories Exotic particles Pharmacy Medical applications Andreas Streun, PSI Industrial applications 5 Why accelerators? → II. Connections Classical Physics Hamiltonian Mechanics Electrodynamics Engineering Radio-frequency Magnet technology Ultra high vacuum Mechanical engineering Alignment & Survey Electronics Control systems Particle Accelerators Modern Physics Quantum mechanics Computing Particle Physics High performance computing Accelerator design codes Digital signal processing s/w Application programming Andreas Streun, PSI 6 Why accelerators? → III. common PP & MR interests Particle Physics (PP) High energy colliders Linear colliders Particle factories Circular colliders Materials Research (MR) Neutrino factories High power proton accelerators Spallation neutron sources Storage rings Photon sources Free electron lasers (FEL) A c c e l e r a t o r s Linear accelerators PP & MR scientists: Andreas Streun, PSI Cyclotrons Synchrotrons understand potential and limitations of accelerators help to specify future machines 7 Particles of interest (PP) Particle Physics: interested in all particles! presently: particular interest in new and unknown particles: W± (80.4 GeV), Z (91.2 GeV), Ho (>115 GeV), ...? produced in e+e− or pp or pp collision highest energies: e.g. LEP, LHC meson pairs (e.g. KSKL, BoBo) at high rate meson factories: e.g. KEK-B, DAΦ ΦNE. muons (µ± ) and neutrinos (νe ,νµ) long baseline experiments: e.g. CNGS, JPARC muon accelerator and neutrino factory projects Andreas Streun, PSI 8 Particles of interest (MR) Materials Research: neutral particles high penetration depth in materials Neutrons (n) penetrate high Z materials depth not a steep function of Z have a magnetic moment and a spin explore structure and dynamics of materials rather low flux (= particles per time and area) Photons (γγ) available at (very!) high flux penetrate well low Z materials have polarization complementary to neutrons (“surface vs. bulk”) Andreas Streun, PSI 9 Particle wavelength Size of probe Size of structure λ ~ 10-10 m MR λ ~ 10-15 m NP De-Broglie wavelength Planck constant h= 6.63·10-34 Js = 4.14·10-15 Particle momentum p = m·v = moc·βγ Andreas Streun, PSI PP λ ~ 10-18 m h λ= p eV·s c < v< v≈c non – relativistic p = mov high relativistic p= moc·γ = Ε /c 10 Recall: momentum & energy Momentum p = m·v = moc·βγ non-relativistic high relativistic Total energy norm. velocity β = v / c Lorentz factor γ = E / moc2 p = mov p = moc·γ = Ε/c Eo = moc2 rest energy E = mc 2 = mo c 2γ = ( mo c 2 ) 2 + ( pc ) 2 = E kin + mo c 2 Kinetic energy Ekin= moc2 (γ−1) = q·U = charge × voltage. Ekin in units of eV is equivalent to the accelerating voltage for a particle with charge q = 1e (p, e+, Na+, µ+...) non-relativistic Ekin = ½ mov2 useful relations: 1 1 high relativistic Ekin = pc β = 1− γ = βγ = γ Andreas Streun, PSI 2 1− β 2 γ 2 −1 11 Examples: momentum and wavelength MR: 1Å neutron (moc2 = 940.8 MeV, mo =1.68·10-27 kg) p = 12.4 keV/c v = 3960 m/s << c Ekin = 0.08 eV <Ekin> = kT temperature equivalent T = 930 K MR: 1Å photon (no rest mass) v = c, Eγ = pc = 12.4 keV NP: 10-15 m electron (moc2 = 511 keV) p = 1.24 GeV/c v = 0.999’999’915 c = c – 90 km/h ! Ekin = pc = 1.24 GeV PP: 10-18 m proton (moc2 = 938.3 MeV) p = 1.24 TeV/c v = 0.999’999’7 c Ekin = pc = 1.24 TeV (→ LHC 7 TeV) Andreas Streun, PSI 12 Particles to accelerate Requirements for acceleration: charge q ≠ 0 and lifetime τ ≥ ≈1 µs standard: electron e− and proton p antiparticles: positron e+ and antiproton p ions: muons: µ+ , µ− (τ = 2.2 µs – hurry up! ) pion π± (τ = 26 ns), neutron n, neutrino ν, photon γ ... Andreas Streun, PSI 13 Particle Production how to get the particles of interest from the particles that can be accelerated Principle Beam on target electrons e− protons p spallation target Andreas Streun, PSI Products how many ? Performance Flux pairs e+e−, pp mesons π → µ → ν neutrons n chapter 8 Colliding beams anything... leptonic e+e− mesons KK, BB... hadronic pp Higgs Ho ? Luminosity Synchrotron radiation electrons e− Brightness chapter 7 photons γ chapter 6 14 A beam of particles Particle beam (n , µ , γ , e−, p ...) = ensemble of N particles in 6-dimensional phase space ( x, y, z; px, py, pz ) 1st order Beam centroid mean values < ri > beam momenta px, py, pz moving along “z” → pz ≈ p >> px, py beam location z (t) beam positions x, y beam angles x’ ≈ px/p, y’ Andreas Streun, PSI 2nd order Beam distribution rms values σi2 = < ri2 > and correlations < ri rj > momentum spread σ∆p/p “bunch length” σ∆z beam sizes σx , σy beam divergences σx’ , σy’ ... correlations ... 15 Beam quality → I. phase space density Criterion for beam quality (n , µ , γ , e−, p ...) : density in 6-d phase space performance of experiment → flux, luminosity, brightness, threshold phenomena → coherence, non-linearity... Theorem of Liouville: (holds under several conditions.... chapter 5 ) ”The 6-d phase space density is an invariant.” or “The 6-d phase space occupied by a beam behaves like an incompressible liquid.” Andreas Streun, PSI 16 Beam quality → II. Emittance Decoupling of 6-d phase space density into 3 × 2 dimensions (this is often ≈ possible): longitudinal × ∆p/p, ∆z momentum spread pulse (bunch*) length * beams are usually “bunched”, not continuous chapter 2 Andreas Streun, PSI horizontal × vertical x, px (or x’) y, py (or y’) transverse emittances εx, εy 2-d phase space area: εx2 = < x2>< x’ 2> − < xx’>2 invariant along beam transport line chapter 5 17 Beam quality → III. Accelerator performance Momentum p ( high relativistic: energy E = pc ) 6-d phase space density Momentum spread σ∆p/p Bunch length σ ∆z Experiment Emittances εx , εy performance: Beam current I = q·dN/dt Luminosity (PP) Higher orders... Brightness (MR) ( non-Gaussian, halo, tails etc. ) Polarization (spin orientation) Time structure: [continuous or] “bunched” → repetition rate Stability: position, angle, momentum, timing... jitter as function of frequency Andreas Streun, PSI 18 PP-experiment → I. Center-of-mass energy p~2 = 0 E1 = E Ecm √ Ecm ≈ 2E m2c2 p = (E1 + E2)2 − (~ p1c + p~2c)2 ~= β Beam on target ~2 c p ~1 c+p E1 +E2 γ= E1 +E2 Ecm p~2 = −~ p1 E1 = E 2 = E Ecm = 2E Colliding beams • Antiparticles: e+, p̄ • possibility of pure leptonic production e+ →← e− • Mesons for experiments: π, K . . . • highest energies (e.g. LHC Ecm = 14 TeV) • Muons and neutrinos: µ [ → νµ] • high luminosity particle factories: Φ, B . . . • Spallation neutrons: n ~ from E1 6= E2 (→ B-factories) • variable boost β Andreas Streun, PSI 19 PP-experiment → II. Luminosity Layout of experiment ~] • Required energy Ecm [ and boost β • Required precision p −→ −→ Events N ≈ 1 p2 E1, E2 p = ∆NN √ ∆N ≈ N • Efficiency of experiment ǫ (Observation inside detector, branching ratio etc.) • Scheduled time of measurement T [s] =⇒ Particle production rate R [s−1] = N ǫT • Production cross section σ [cm2, or barn = 10−24 cm2] =⇒ R = σL Andreas Streun, PSI Luminosity L [cm−2s−1] 20 Luminosity = sum of all possible encounters per time and area N1 N2 × ∗ L= T A (A∗ common interaction area) L = particle current of beam 1 × particle density of beam 2 Requirements for PP-machines • high beam currents: N1, N2, T • focus at collision: A∗ • (highest ↔ given) beam energies: E1, E2 −→ ~ Ecm [,β] =⇒ challenges for accelerators. Andreas Streun, PSI 21 “Livingston plot” Progress of center of mass energy Andreas Streun, PSI Luminosities of e+e−-colliders 22 2. Accelerator basics and types Particle sources Electric and magnetic fields Electrostatic accelerators Marx Cockcroft-Walton van der Graaff Radio-frequency acceleration Linear accelerators Linac Buncher Linear collider FEL Recirculation 1: fixed magnetic field and variable orbit Recirculated linac Microtron Cyclotron FFAG Recirculation 2: variable magnetic field and fixed orbit Betatron Synchrotron and storage ring Light sources Circular colliders The LHC Andreas Streun, PSI 23 Particle sources → I. Electron sources thermionic cathode laser cathode (photo effect) field emission gated field emitter (MIT) field emitter array with a damage Andreas Streun, PSI 24 Particle sources → II. Proton [ion] sources plasma ion source laser ion source electron beam ion source Andreas Streun, PSI 25 2.Accelerator basics and types Electric and magnetic fields How to accelerate ? Lorentz Force: d~s ~v = dt ~ + E), ~ F~ = q (~v × B path Kinetic energy gain ∆T = work on the particle: ∆T = W = Z F~ · d~s = q Z d~s ~ ×B dt | {z =0 Z ~ · d~s · d~s +q E | {z } } =U =⇒ Electric field to accelerate particles: Kinetic energy gain = charge × voltage: ∆T = qU Andreas Streun, PSI 26 2.Accelerator basics and types Electric and magnetic fields The most simple electron accelerator color-TV tube: 27 kV X-ray tube: ≈ 100 kV Andreas Streun, PSI 27 2.Accelerator basics and types Electric and magnetic fields What are magnetic fields good for? ~ = F~ = p~˙ = m~v˙ q ~v × B ~ = Bz e~z assume B −→ since ṁ = 0 (no energy gain). q v̇x = vy Bz m q v̇y = − vxBz m v̇z = 0 =⇒ [d/dt . . .] Oscillation of velocities vx(t) = vxo cos(ωt) + vyo sin(ωt) vy (t) = vyo cos(ωt) − vxo sin(ωt) vz (t) = vzo q Cyclotron frequency ω = m Bz =⇒ Helical trajectories (closed circles for vzo = 0) x(t) = xo + ρ cos(ωt − φ) y(t) = yo + ρ sin(ωt − φ) z(t) = zo + vzot Andreas Streun, PSI Radius of curvature ρ = tan φ = √ m 2 +v 2 vxo yo qBz vyo vxo 28 2.Accelerator basics and types Electric and magnetic fields Magnetic vs. electric deflection ~ ⊥ ~v B v→c ~ → F = q(vB + E) k E → F ≈ q(cB + E) [1 MeV e− : v = 0.86c] Technical limitations: electric fields: Emax ≈ 107 V/m (10 kV/mm) magnetic fields: Bmax ≈ 2 T (normalconducting)/10 T (superconducting) −→ cBmax ≈ 100 × Emax =⇒ Magnetic fields for deflection (bending and focussing) =⇒ Electric fields for acceleration. (In special cases, electric fields too are used for deflection). Andreas Streun, PSI 29 2.Accelerator basics and types Electrostatic Accelerators Cathode ray tubes (<1900) −→ DC (”direct current”) electron guns Example: 100 keV Teststand for LEG (”Low Emittance Gun”) Characterization of field emitter array type cathodes for SwissFEL project. Andreas Streun, PSI =⇒ Increase voltage ! =⇒ 30 2.Accelerator basics and types Electrostatic accelerators Cascaded high voltage generators Marx Generator (1920) Principle first arc trigger fires all arcs and connects capacitors in series. Un = nUo • high voltage • high current • short pulses • low duty cycle Umax ∼ 6 MV Andreas Streun, PSI Cockcroft Walton (1930) Principle diodes shift up voltage offset on capacitor chain. Un(t) = 2nUo +Uo sin(ωt) • quasi DC HV • with AC ripple Umax ∼ 4 MV 31 2.Accelerator basics and types Electrostatic accelerators PSI Cockcroft Walton 870 keV proton source Andreas Streun, PSI 32 2.Accelerator basics and types Electrostatic accelerators Van der Graaff Generator (1930) Principle corona discharge sprays charge on belt. charge is accumulated on high voltage dome. current through resistor chain stabilizes voltage. accelerator: resistor column = beam tube Umax ∼ 10 MV Andreas Streun, PSI 33 2.Accelerator basics and types Electrostatic accelerators Tandem van der Graaff Principle inversion of ion charge by stripper foil =⇒ double (H − → H +) or multiple (ions) energy. 6 MV ion tandem van der Graaff at ETHZ Andreas Streun, PSI 34 2.Accelerator basics and types Electrostatic accelerators Voltage limitations Maximum DC voltage U ∼ 10 MV technical limitations: discharge, insulation etc. =⇒ maximum particle [kinetic] energy T = qU < 10 MeV for protons and electrons (q = ±e). (multiply charged ions: |q/e| > 1 −→ some 10 MeV) PP requirements W ± and Z production: 100 GeV e+ ↔ e− Higgs and unknowns: > TeV protons! how to accelerate further ? Andreas Streun, PSI 35 2.Accelerator basics and types Radio-frequency (RF) acceleration AC/RF acceleration (Ising 1925, Wideröe 1928) RF (”Radio Frequency”) = high frequency AC (“Alternating Current”): MHz . . . GHz Drift tube length (v ≪ c): Ln = U = Uo sin(ωt + φ) −→ τ 2v = τ 2 q 2T mo = τ 2 q 2nqUo sin φ mo T = nqUo[sin φ] basically unlimited! Phase φ: maximum acceleration for φ = π2 , but . . . Andreas Streun, PSI 36 2.Accelerator basics and types RF-acceleration Phase focussing Kinetic energy gain for synchronous particle (t̂ = 0) T̂ → T̂ + qUo sin φ Consider particles arriving too early (t < 0) or too late (t > 0): T → T + qUo sin(φ + ωt) ≈ T + qUo sin φ + ωqUo cos φ · t; 0 < φ < π/2 → |t| ≪ τ acceleration and cos φ > 0: late particles get more energy early particles get less energy −→ −→ faster; catch up with synchronous particle slower; wait for synchronous particle =⇒ Stability – within some interval [tmin, tmax] = the bucket =⇒ Bunched beam: In RF accelerators, the beam is not continuous but distributed on separate bunches. v→c Temporal spacing τ = 2π/ω, longitudinal spacing vτ −→ λrf . Andreas Streun, PSI 37 2.Accelerator basics and types RF-acceleration Phase focussing: a simple tracking sub-relativistic linac: cell length adjusted to reference particle velocity v̂: q Ln = τ2 v̂n, v̂n = 2mT̂on , T̂n = nUo sin φ. Tracking recursion: Tn = p Tn−1 + Uo sin(φ + ωtn−1) vn = 2Tn/mo tn = tn−1 + Ln(v̂n − vn) Parameters: Uo = 0.1, τ = 1, mo = 1 Starting conditions: to = (−0.1 . . . +0.1)τ Phase φ → π/2: maximum energy but small bucket: large beam loss Lower phase, larger bucket: particles perform stable oscillations during acceleration. Andreas Streun, PSI 38 2.Accelerator basics and types RF-acceleration Linear accelerator (``Linac'') Electromagnetic wave travelling through disk loaded wave guide: ! phase velocity of wave = particle velocity cell radius R given by frequency (first zero of radial Bessel function) cell length ∆z determines phase velocity: phase advance per cell disk iris: aperture for wave and beam propagation Andreas Streun, PSI 39 2.Accelerator basics and types RF-acceleration Accelerating structures Drift tube linacs ⊲ for v ≪ c (protons, ions) ⊲ frequency ∼ 100 MHz ⊲ gradient 1 . . . 10 MV/m Travelling wave linac ⊲ ⊲ ⊲ ⊲ for v ≈ c (electrons) frequency ∼ 3 GHz pulsed (few µs, 10 . . . 100 Hz repetition) gradient 10 . . . 50 MV/m Standing wave structures / RF cavities ⊲ continuous operation possible: −→ circular machines ⊲ frequency ∼ 100 MHz . . . 3 GHz ⊲ gradients ∼ 1 MV/m Andreas Streun, PSI 40 2.Accelerator basics and types Linear accelerators Linacs Stanford 100 GeV electron/positron linac collider SLC Argonne National Lab 50 MeV proton linac of drift tube type Andreas Streun, PSI Superconducing linac structure from Accel company 41 2.Accelerator basics and types Linear accelerators Bunching Buncher: short linac or cavity at φ ≈ 0 Andreas Streun, PSI → ∆T = qU sin(ω∆t) ≈ ωqU ∆t 42 2.Accelerator basics and types Linear accelerators SLS 100 MeV electron linac Andreas Streun, PSI 43 2.Accelerator basics and types Linear accelerators Linear colliders why? • e+e− collisions complementary to pp or pp̄ (LHC) • energy limit for circular e+e− colliders reached (LEP) =⇒ ILC (“International Linear Collider”) Ecm = 500 GeV [ → 1 TeV] =⇒ GDE (“Global Design Effort”): merge NLC(USA), GLC(J), TESLA(EU) Costs are main design criterion! A linear collider’s maximum energy is not physically limited but just by costs (and earth’s surface curvature . . .) ← ILC with superconducting linacs, gradient ≈ 35 MV/m. Future: CLIC at CERN: Ecm → 3 TeV in L < 30 km based on new accelerator concept for > 100 MV/m gradient. Andreas Streun, PSI 44 2.Accelerator basics and types Linear accelerators Free electron laser prepare electron beam of very high phase space density : low transverse emittances, very short pulse, low energy spread =⇒ coherent emission of synchrotron light and self-amplification (−→ ch.6) 1 Å X-ray pulses: pulse length t < 100 fs, power > 10 GW In operation: LCLS (SLAC/USA), FLASH (DESY/DE). Planned: SwissFEL (PSI/CH) ! LCLS undulator line −→ =⇒ Linac development is common PP and MR interest. Andreas Streun, PSI 45 2.Accelerator basics and types Recirculation 1 Recirculated Linacs Economic re-use of linac Constraints: time of flight for recirculation track ! ∆ta→a = nτrf n∈N linac pulse > total travel time ∆Ta→a→b −→ or c.w. (“continuous wave”) operation. Andreas Streun, PSI 46 2.Accelerator basics and types Recirculation 1 S-DALINAC (Darmstadt, D) 130 MeV 2× recirculated s.c. linac for free electron laser and nuclear physics CEBAF (“Continuous Electron Beam Accelerator Facility”) 6 GeV 5× recirculated double s.c. linac for nuclear physics (Newport News, USA) Andreas Streun, PSI 47 2.Accelerator basics and types Recirculation 1 The Microtron / racetrack microtron Electrons only! (β → 1) Original microtron Time of flight for track k Lorentz force mv 2 R = evB tk = v≈c −→ Racetrack microtron 2πRk +2L c Rk = (Rk bending radius) mo γk c eB = Ek eBc −→ tk = Time difference from one turn to next: ∆t = tk+1 − tk = Microtron condition: Andreas Streun, PSI 2π eBc2 2πEk eBc2 + 2cL ! (E − E ) = nτrf | k+1{z k} =∆Elinac ∆E/e [MeV] × frf [GHz] = 14.3 n B [T] 48 2.Accelerator basics and types Recirculation 1 MAMI (”MAinz MIcrotron”) (Mainz, D) Cascade of 3 racetrack microtrons and 1 double sided microtron: 3.5 MeV −→ 14 MeV −→ 180 MeV −→ 850 MeV −→ 1.5 GeV MAMI-RTM3 (850 MeV): n = 1, frf = 2.5 GHz, B = 1.3 T, ∆E = 7.5 MeV Andreas Streun, PSI 49 2.Accelerator basics and types Recirculation 1 The Cyclotron (Lawrence/Livingston 1932) protons and ions only! (β ≪ 1) Original cyclotron Sector cyclotron (PSI) Lorentz force: mo v 2 R = evB −→ recirculation time t= 2πR v = 2πmo eB t no function of energy (for β ≪ 1) −→ isochronous machine cyclotron frequency Andreas Streun, PSI ωc = 2π t = e mo B ! Constraint: ωrf = nωc 50 2.Accelerator basics and types Recirculation 1 Cyclotrons ← Lawrence’s first 80 keV cyclotron from 1932 (≈ 15 cm diameter) → Livingston and Lawrence at the 70 cm cyclotron, Berkeley 590 MeV proton cyclotron cw operation at 2 mA proton current =⇒ > 1 MW proton beam power! world's most powerful accelerator! Driver for SINQ (Swiss Spallation Neutron Source) Andreas Streun, PSI 51 2.Accelerator basics and types Recirculation 2 The Betatron (Kerst 1940) ⇐= Recirculation =⇒ fixed B-field, variable radius variable B-field, fixed radius microtron and cyclotron betatron and synchrotron ~˙ ~ = −B (Maxwell) The Betatron: rotE ~ = B(r, t)~ez B-field varies in radius and time: B H RR ˙ ~ ~ t) · ~ez rdrdφ Stokes: E(t) · ~eφ ds = − B(r, 2 ~˙ 2πRE(t) = −hB(t)iπR → E = Eφ = − 12 RhḂi Lorentz force bends: Electric force accelerates: mv = p = eRB(r=R) ṗ = F = eE = 12 eRhḂi =⇒ Betatron equation: Ḃ = 21 hḂi or B(t) = 12 hB(r, t)i + Bo acceleration on a circle of constant R (given by Bo) [ gradient dBdr(r) |R provides vertical focussing ] Kerst at his betatron. Andreas Streun, PSI inductive acceleration without RF! 52 2.Accelerator basics and types Synchrotrons The Synchrotron mv 2 R = qvB −→ p = qRB (Veksler, McMillan 1945) −→ p(t) = qRB(t) Momentum follows magnet field variation due to RF phase focussing: • inject beam into ring at Bo with momentum po = qRBo • increase B-field −→ B + ∆B • bending radius shrinks by ∆R < 0 • path becomes shorter by 2π∆R • particles arrive earlier by ∆t = 2π βc ∆R <0 • RF cavity: U (∆t) = qUo sin(ω∆t + φ) > 0 for ∆t < 0 if φ ≈ π • acceleration by ∆p = βqU (∆t) =⇒ self-synchronisation of p(t) with B(t) ! Constraints: φ ≈ π and 2πR = nβλrf • extract beam at Bmax with momentum pmax = qRBmax Andreas Streun, PSI 53 2.Accelerator basics and types Synchrotrons The storage ring storage ring = synchrotron at constant energy (momentum) accumulate and store beam for long time (hours) −→ synchrotron photon source −→ ∆E = qUo sin φ − ∆Eloss = 0. only∗) for compensation of losses due to synchrotron radiation, wake fields etc. ∗) Electron storage ring: radiated power: (E [GeV])4 × I [mA] P [W] = 88.5 R [m] E I R = beam energy = beam current = radius of path in dipoles e.g. LEP (“Large Electron Positron collider”): Beam energy E = 100 GeV, beam current I ≈ 2 × 5 mA B = 0.11 T → R = 3 km; ≈ 70% magnet filling → circumference 27 km! Synchrotron radiation power ≈ 30 MW, requires > 60 MW electric. =⇒ upper energy limit for electron rings. No problem with protons −→ LHC Andreas Streun, PSI 54 2.Accelerator basics and types Synchrotrons Circular collider circular collider = one or two storage rings with opposite beams of particles • ↔ • and energies E, E single ring 2n interaction points 2 × n bunches • = ¯• E = E Andreas Streun, PSI double rings 1 or 2n IPs, > 2n bunches avoid parasitic collisions or close encounteres allows • 6= ¯ • E 6= E ”brezel” scheme 1 or few IPs orbit oscillations to avoid parasitic collisions. • = ¯• E = E 55 2.Accelerator basics and types Synchrotrons Synchrotrons • Pure synchrotrons: [accumulation], acceleration and extraction ⊲ booster synchrotrons to fill storage rings: SPS→LHC. ⊲ beam on target for experiments (pulsed): SPS→CNGS. • Damping rings: accumulation, damping and extraction ⊲ damping rings for linear colliders: SLC, ILC. • Storage rings: accumulation, [acceleration], damping and storage ⊲ antiproton accumulator: AD, AA at CERN. ⊲ light sources: store beam and use radiation: AURORA, SLS, ESRF. • Circular colliders: accumulation, [acceleration], storage and collision ⊲ classic single ring AdA or double ring VEP-1. ⊲ high energy frontier: LEP e+ ↔ e−, LHC p ↔ p. ⊲ particle factories: DAΦNE, KEK-B, LEP. + + ⊲ special: HERA e− ↔ p, RHIC Au ↔ Au , muon colliders µ+ ↔ µ−. Andreas Streun, PSI 56 2.Accelerator basics and types Synchrotrons Synchrotron light sources AURORA 0.65 GeV, π m SLS 2.4 GeV, 288 m SPRING-8 8 GeV, 1436 m first synchrotron light from the SLS, 15.12.2000 Andreas Streun, PSI 57 2.Accelerator basics and types Synchrotrons Circular colliders ← AdA Frascati, 1962 First e+e− collisions VEP-1 → Novosibirsk, 1964 First double ring collider e−e− Tevatron (FNAL, USA) 2× 1 TeV pp̄ ւ † SSC (Texas, USA) 2× 20 TeV pp̄ 87 km circumference 1988 approval 1989 construction start 1993 cancelled Andreas Streun, PSI 58 2.Accelerator basics and types Synchrotrons Particle factories Particle factory = collider for maximum luminosity at fixed energy. + − DAΦNE (Frascati, Italy). 2×510 MeV e e . KEK-B (Tsukuba, Japan), 8 GeV e− ↔ 3.5 GeV e+ . PEP-B (SLAC, USA), 9 GeV e− ↔ 3.1 GeV e+ . Andreas Streun, PSI 59 2.Accelerator basics and types Synchrotrons CERN accelerators Andreas Streun, PSI 60 2.Accelerator basics and types Synchrotrons previous slide: right/top: LEP/LHC aerial view right/bottom: LEIR (”Low Energy Ion Ring”) LEP “Z-factory” (1989-2000) copper cavities → SPS tunnel ց CNGS (”Cern Neutrinos to Gran Sasso”) ↓ Experiment at the SPS Andreas Streun, PSI 61 2.Accelerator basics and types Synchrotrons LHC the Large Hadron Collider synchrotron & storage ring 26′658.883 m circumference. 1232 superconducting dipole magnets: current 12 kA, temperature 1.9 K Operating cycle: 1. Injection & accumulation (∼minutes) 450 GeV protons from SPS 2. Acceleration (≈ 15 minutes) E = 450 → 7000 GeV B = 0.535 → 8.33 Tesla 3. Collider operation: p =⇒ ⋆ ⇐= p Data acquisition (∼ hours) 4. Deceleration =⇒ 1. First operation August 2008 =⇒ accident! Restart Nov.2009 at 3500 GeV. Luminosity Oct.2011 L = 3.4 × 1033 cm2 s−1 Andreas Streun, PSI 62 Beam Dynamics Overview Andreas Streun, PSI 63 3. Transverse Beam Dynamics ⊲ Foundations Coordinate system. The Hamiltonian. Approximations. Field expansion. Magnet rigidity. Transfer matrix. Examples. ⊲ Magnets Iron magnets: Dipole. Bending magnet. Quadrupole. Superconducting magnets: LHC-dipole. Focusing in both planes: Solenoid. Quadrupole doublet. ⊲ The Lattice Concatenation. Composition. Components. Space. ⊲ Betatron oscillations Twiss parameters. Normalized coordinates. Periodicity. Applications: FODO cell. Circular test collider. ⊲ Imperfections Resonances: the tune diagram. Orbit distortion. Chromaticity. Andreas Streun, PSI 64 3. Transverse beam dynamics Foundations How to proceed: [Usually] only magnetostatic fields are used for deflection: ¨ = q~x˙ × B(~ ~ x) Lorentz-force F~ = m~x with m = moγ = const., resp. p = |~ p| = const. in principle: ~ x) , ~xo , p~o B(~ =⇒ ~x(t) , p~(t) −→ done. Transverse beam dynamics • Formalism for discrete magnets: (~ x ; p~)in → (~x ; p~)out • Concatenation of magnets: M1 ◦ M2 ◦ . . . =⇒ the Lattice • Formalism for an ensemble of particles { (~ x ; p~)i } Andreas Streun, PSI i = 1...N 65 3. Transverse beam dynamics Foundations Theoretical foundations (outline) A. Define a curvilinear coordinate system: the curve is the reference orbit of the accelerator. B. Transform the Hamiltonian to the curvilinear system. C. Introduce approximations for simplification: e.g. particle stays always close to the curve. D. Use expansion of the magnetic field near curve. E. Arrive at a simplified Hamiltonian. multipoles can be treated separatedly. F. Derive transfer matrices for linear magnets: analogy to ray optics. Andreas Streun, PSI 66 3. Transverse beam dynamics Foundations A. Coordinate system Curve in space: position ~ro(s) curvature ~h(s) h = 1 ρ torsion τ (s) path length s from arbitrary point ˆ ~s = d~ro(s)/ds tangent unit vector ˆ = −~h(s)/h(s) curvature unit vector ~x ˆ ˆ ˆ ~y = ~s × ~x ˆ ; ~ˆs; ~yˆ} {~x orthogonal curvilinear system ˆ + y~yˆ Points close to the curve: ~r(x, s, y) = ~ro(s) + x~x Transformation of vector ~a from cartesian to curvilinear: ˆ] ˆ as = ~a · [(1 + hx)~ˆs + τ x~yˆ − τ y~x ax = ~a · ~x ay = ~a · ~yˆ [in most cases τ = 0 (planar curve) and h = const. or h = 0 (cylindric resp. cartesian geometry) ] Ref.: E.D.Courant & H.S.Snyder, Theory of the alternating gradient synchrotron, Ann. Phys. 3 (1958) 1 Andreas Streun, PSI 67 3. Transverse beam dynamics Foundations B. The Hamiltonian H =T +U sum of kinetic and potential energy [usually]. =⇒ equations of motion ẋ = ∂H ∂px ṗx = − ∂H ∂x in canonical variables ~x, p~ relativistic Hamiltonian of a particle in electromagnetic fields q ~ 2 H = qV + c (moc)2 + (~ p − q A) ~ the canonical momentum with p~ = m~v + q A ~ = −grad V − ∂ A~ , E ∂t ~ = rot A ~ −→ B ˙ v ) = q (E ~ + ~v × B) ~ (m~ Ref.: H.Goldstein, Classical mechanics −→ transformation of H into curvilinear {x; s; y}system Andreas Streun, PSI 68 3. Transverse beam dynamics Foundations C. Approximations Approximations valid for large high-energy machines, e.g. LHC, SLS • paraxial • adiabatic x, y “small” −→ ~ expansion of B-field near curve. T (t) slowly varying • small curvature • planar curve −→ ≈ constant. x ≪ ρ or xh ≪ 1. torsion τ = 0. • piecewise constant fields no fringes: Ax = Ay = 0 → px;y = mvx;y . • arcs & straights • ultrarelativistic piecewise constant or zero curvature h(s). β = 1, E = pc −→ s = ct. . . . continue with simple model, but stay aware of the approximations! Andreas Streun, PSI 69 3. Transverse beam dynamics Foundations D. Field expansion ~ = rotA ~ → By + iBx = B ∂ +i ∂ − ∂x ∂y As P 1 q iφn A = −ℜ s p n (ian + bn )re By (x, y) + iBx(x, y) = (Bρ) X reiφ = x + iy (ian + bn)(x + iy)n−1 n 2n-pole magnets: n = 1, 2, 3 . . . = dipole, quadrupole, sextupole. . . multipole moments: bn regular, an skew (rotated by 90◦/n) e.g. quadrupole (n = 2): By (x) = (Bρ) b2 x Bx(y) = (Bρ) b2 y Magnetic rigidity: Regular multipole: Poletip field: Bρ = bn = p q = βE/e ne c 1 ∂ 1 Bρ (n−1)! = β ne 3.3356 By (x,y ) ∂xn−1 (n−1) Bpt = (Bρ)bnR n−1 = y =0 Rn−1 ∂ (n−1)! R = pole inscribed radius Andreas Streun, PSI E[GeV] By (x,y ) ∂xn−1 (n−1) y =0 70 3. Transverse beam dynamics Foundations Magnetic rigidity (Bρ) ρ = bending radius v = velocity Lorentz force = centrifugal force: qvB = p q p = mv =⇒ (Bρ) = p = mocβγ, E = moc2γ B = magnetic field q = nee = charge mv 2 ρ (relativistically valid) −→ p= βE c =⇒ (Bρ) = βE ne ec E is given in eV units: 1 eV = 1.6 · 10−19 |As{z· V} Joule (Bρ) = β ne c · E[ J]/e = β ne c E [eV] = β ne · 109/c ·E [GeV] | {z } 3.3356 s/m s · V = Vs · m = T · m Units: [ (Bρ) ] = m m2 Andreas Streun, PSI 71 3. Transverse beam dynamics Foundations E. The simplified Hamiltonian p2x + p2y b21(s) 2 b2(s) 2 2 b3(s) 3 −b1(s)xδ+ x+ (x −y )+ (x −3xy 2)+. . . H(x, px, y, py ; s) = 2(1 + δ) 2 2 3 δ := p−po po . [H] = [p] = 1. sin x′ = px p = px (1+δ )po ≈ x′ (paraxial). Linear equations of motion with nonlinear sextupole term px dx ∂H = = x = ds ∂px 1 + δ ′ p′x = ∂H dpx =− = b1δ − (b21 + b2)x −b3(x2 − y 2) ds ∂x p′y Andreas Streun, PSI py y = 1+δ ′ ∂H dpy =− = b2y +2b3xy = ds ∂y 72 3. Transverse beam dynamics Transfermatrix F. Transfermatrix Example: Drift space, bi = 0 ∀ i p′x = 0 x′ = px 1+δ = px p −→ x′(s) = x′o, x(s) = xo + x′os Write as a matrix: x x′ = xo 1 s · 0 1 x′o Example: Quadrupole, b2 6= 0, assume b2 > 0 and δ = 0 x′ = px −→ x′′ = −b2x −→ harmonic oscillator: √ √ √ √ √ x′o ′ ′ √ x(s) = xo cos( b2s) + b sin( b2s) x (s) = −xo b2 sin( b2s) + xo cos( b2s) p′x = −b2x 2 Matrix notation: p′y = +b2y Andreas Streun, PSI ′ x x′ y = py = −→ cos φ √ − b2 sin φ y y′ = sin φ x · xo′ o cos φ √1 b2 √ cosh φ b2 sinh φ φ := p b2 s sinh φ y · yo′ o cosh φ √1 b2 73 3. Transverse beam dynamics Transfermatrix Quadrupole in thin lens approximation: √ Length s = L ”small”, but b2L = const. = x x′ y y′ = = 1 − f1 1 1 f 0 1 x = b1 1+δ δ − b21 1+δ x Dispersion: dx D(s) = dδ o = D′(s) = sin φo 1 b1 (1 f = focal length. x · xo′ o 0 yo · 1 yo′ Example: Dipole sector, b1 6= 0, δ 6= 0 ′′ 1 f, b1 = h δ −→ x(s) = xo cos φ + x′o sin φ + 1+ b1 (1 − cos φ) δ φ := √b1 s 1+δ − cos φo) φo = b1s p′y = 0 −→ y(s) = yo + yo′ s (like drift space) Andreas Streun, PSI 74 3. Transverse beam dynamics Transfermatrix Bending magnet transfer matrix General regular (ai = 0 ∀ i), linear (ai = bi = 0 for i ≥ 3) magnet: Dipole with gradient: b1 6= 0, b2 6= 0; δ 6= 0 √1 sx c 0 x x K √ ′ cx 0 − K sx x y = 0 0 cy ′ √ y 0 0 − −b2 sy δ out 0 0 0 √ with: cx[sx] = cos [sin]( K L), cos ix = cosh x sin ix = i sinh x b1 K 0 0 √1 −b2 sy cy 0 (1 − cx) √b1 sx K 0 0 1 √ cy [sy ] = cos [sin]( −b2 L), −→ x x′ y · ′ y δ in K = b21 + b2 can be focussing or defocussing Special cases: b2 = 0 → Dipole b1 = 0 → Quadrupole b1 = 0 and b2 = 0 → Drift 0 < −b2 < b21 → synchrotron magnet, focussing in x and y [ Alternative namings and conventions: Andreas Streun, PSI h= 1 ρ = b1 k = +b2 or k = −b2 ] 75 3. Transverse beam dynamics Magnets Magnet design: I. Iron magnets ~ = ~j rotH no conductors in beam area: j = 0 ~ = rot grad = 0 → define magnetostatic scalar potential Φ: H 1 µo gradΦ consider iron/air boundary: ~ = 0 → Biron = Bair → Hiron = 1 Hair divB µr H Rb Ra Rb 0 = H ds = a Hair ds + b Hiron ds ≈ a Hair ds = 0 −→ Φa = Φb =⇒ iron surfaces are magnetic equipotentials. ~ = div gradΦ = ∆Φ = 0 = divB ∂ 2Φ ∂x2 + ∂ 2Φ ∂y 2 for long magnet, i.e. ∂Φ ∂s =0 ~ B(x, 0) = By (x, 0)~ˆey due to symmetry. Design requirement: By (x, 0) = f (x) R R Ansatz: By (x, y) = f (x) + g(y) −→ Φ = By dy = f (x)y + g(y) dy ∆Φ = ∂ 2 f (x) y ∂x2 + ∂g (y ) ∂y =0 =⇒ Φ(x, y) = f (x)y − Andreas Streun, PSI −→ 2 1 ∂ f (x) 3 6 ∂x2 y g(y) = − R ∂ 2 f (x) y dy ∂x2 ~ −→ B(x, y) = = 2 1 ∂ f (x) 2 − 2 ∂x2 y ∂ Φ(x,y ) ˆ ex ∂x ~ + ∂ Φ(∂yx,y)~ˆey 76 3. Transverse beam dynamics Magnets Iron dominated dipole magnet By (x, 0) = Bo = f (x) −→ Φ = Boy, Bx = 0 equipotentials parallel to x-axis → flat poles. H Hds = RR A= jc da B 2jc =⇒ g Siron + µoµr µo Coil cross section A µr ≫1 −→ A ≈ Bg 2jcµo jc [A/m2] current density, g [m] gap, µo = 4π · 10−7 Vs/Am, µr permeability. Andreas Streun, PSI 77 3. Transverse beam dynamics Magnets Bending magnet Basic parameters: Field B on reference arc p B with (Bρ) = → curvature h = ρ1 = (Bρ ) q for a certain momentum, resp. energy pc = βE Length L along reference arc → bending angle φ = hL = Lρ 8◦ rectangular bending magnet of the SLS for electrons of max. 2.7 GeV. Further parameters: Edge angles ζ1, ζ2 ζ = 0, edge ⊥ beam: sector bend ζ = φ2 : rectangular bend (most common type, made from stacked laminates) ∂B ∂B y 1 Gradient ∂xy → quadrupole moment b2 = (Bρ ) ∂x → synchrotron magnet focusing in both x and y for field index n = − bb22 ∈]0, 1[ 1 Andreas Streun, PSI Gradient bending magnet of the SLS booster synchrotron for bending and horizontal focussing. 78 3. Transverse beam dynamics Magnets Quadrupole linear field: By (x, 0) = gx, with g = ∂By ∂x the field gradient. Magnetostatic potential Φ = gxy =⇒ equipotentials are hyperbolas By (x, y) = gx, Ideal hyperbolic poles Bx(x, y) = gy approximation by hyperbolic sections SLS storage ring quadrupole Quadrupole is focusing in one plane, defocusing in the other plane. Andreas Streun, PSI 79 3. Transverse beam dynamics Magnets Magnet Design: II. superconducting magnets Dipole Quadrupole B>2T −→ iron saturated. =⇒ Field from current distribution: I ∼ cos φ −→ dipole field I ∼ cos 2φ −→ quadrupole field etc. Ideal current shells =⇒ iron yoke only for return flux s.c. magnets vs. iron magnets: Approximation by discrete coils • Field strength: ≈10 T vs. ≈2 T • Field homogeneity: ∆B/B ≈ 10−3 vs. ≈ 10−4 • Cryogenics (LHC: T = 1.9 K) Figures taken from: S.Russenschuck, Design of accelerator magnets, CERN-2005-004 Andreas Streun, PSI 80 3. Transverse beam dynamics Andreas Streun, PSI Magnets 81 3. Transverse beam dynamics Magnets How to focus in both planes H Quadrupole: H ds = 0 Homogenous current density both planes: j(x, y) = j −→ By = H H ds = j 6= 0 at beam. µo j 2 x, Bx = − µ2oj y Lithium lens Liquid lithium (Z = 3) in beryllium (Z = 4) cylinder, used for focussing of antiprotons or positrons at pair production target. Focusing by the beam’s self-field coasting beam with homogeneous current, resp. charge density ~j = v̺~ˆes ~ = ̺, divD ~ = ~j, rotH ~ + ~v × B) ~ F~ = q(E Focusing by colliding beam of antiparticles −→ Fr = + q 2µβo2vγj2 r > 0 ̺ → −̺, ~v = −~v → ~j = ~j strong but nonlinear “lens”: Bx(y) vs. y → beam-beam focusing → luminosity limitation for circular colliders Andreas Streun, PSI 82 3. Transverse beam dynamics Magnets Solenoid ~ = Bo~ˆes k ~v main field: B → basically no focusing ~ ≈ Br~ˆer ⊥ ~v fringe field: B → azimuthal kick → ~v ≈ vo~ˆes + vφ~ˆeφ → Fr ∼ vφ × Bo~ˆes < 0 ~ = 0 and Use divB 0=− −→ R r R 2π 0 0 R s1 so R V ~ dV = divB Bs(so) r dr dφ + | {z } =0 R r R 2π 0 0 Br (s) ds = − B2or R ∂V ~ · d~a B (Gauss) Bs(s1) r dr dφ + | {z } =Bo in fringe field: R s 1 R 2π so 0 Br (s) r ds dφ Azimuthal kick on particle when passing the fringe field with po = mvo p~ = q Z t1 to Andreas Streun, PSI ~ dt = q ~vo × B Z s1 so ds Br dt ~ˆeφ dt qBo −→ vφ = − r 2m 83 3. Transverse beam dynamics vφ = rφ̇ = rφ′vo Magnets o −→ φ′ = − 2qB mvo −→ φ(s) = −κs with κ := qBo 2mvo = ωc 2v o Radial force = Lorentz force − centrifugal force: F~ = (qvφBo − mvφ2 /r) ~ˆer −→ Fr = − qBo 2m 2 r 2 qBo r −→ r(s) = ro cos κs + ro′ sin κs 2mvo =⇒ Solenoid provides beam rotation and linear focusing in both planes. Fr = mr̈ = mr′′vo2 −→ r′′ = − Transfermatrix for x = r cos φ, x′ = r′ cos φ, y = r sin φ, y ′ = r′ sin φ: x C ′ 0 x = −S y 0 y ′ out | 0 S C 0 0 C −S 0 {z Rotation with C = cos φ(s), S = sin φ(s). Andreas Streun, PSI 0 C S/κ 0 0 S −S · κ C 0 0 · · 0 0 0 C S/κ C 0 0 −S · κ C } | {z } Focusing x x′ y y ′ in 84 3. Transverse beam dynamics Magnets Quadrupole doublet alternating gradient (AG) focussing a quadrupole focusses in one plane and defocusses in the other plane. → add another quadrupole of opposite polarity [and same strength]: Mx,y = 1 ± f1 x, y x′, y ′ = Mx,y out x, y x′, y ′ in Mx,y = quad.(±) · drift(L) · quad.(∓) ! L L 1∓ f 0 1 0 1 L 1 · 0 1 · ∓ f1 1 = − fL2 1 ± L f =⇒ −L/f 2 provides focusing in both planes. 1 dx,y 0 1 Distances dx,y to foci: 2 L f ! xo, yo 0 · Mx,y · = −→ d = 1 ∓ x,y 0 ∗ f L Constraint L < f for double focus: dx > 0 and dy > 0 Andreas Streun, PSI 85 3. Transverse beam dynamics Lattice Concatenation of elements element → element transformation: translation and rotation ~xn,in = T~ + R~x(n−1),out Ideal lattice: T~ = ~0, R = {1} Edge focussing Laminated magnets: edges rotated by ζ = Φ/2. Horizontal: geometry effect Vertical: Bx in fringe field Andreas Streun, PSI x x′ y = y ′ out 1 tan ζ R 0 0 0 0 1 0 0 1 ζ−Ψ) 0 − tan(R 0 x ′ 0 x · 0 y y ′ in 1 Ψ depends on fringe field shape. 86 3. Transverse beam dynamics Lattice Lattice composition Andreas Streun, PSI 87 3. Transverse beam dynamics Lattice The Lattice Lattice = [closed] connection of accelerator components Component Drift space Dipole Quadrupole Sextupole Solenoid Corrector dipole Kicker magnet RF cavity Undulator Parameters Length L L field By . . . L, field gradient ∂By /∂x L, field curvature ∂ 2By /∂x2 L, field Bs R R int. fields By ds (CH), Bx ds (CV) R int. field pulse B(t) ds wavelength λrf , voltage Vrf period length, peak field, gap Purpose free space bending focussing chromaticity correction focussing [+rotation] beam steering injection & extraction acceleration synchrotron light + diagnostic elements: beam position monitors, current transformers etc. + vacuum elements: flanges, bellows, radiation absorbers etc. Andreas Streun, PSI 88 3. Transverse beam dynamics Lattice Synchrotron light source components Andreas Streun, PSI 89 3. Transverse beam dynamics Andreas Streun, PSI Lattice 90 3. Transverse beam dynamics Lattice Space requirements A lattice section . . . ↑↑ as seen by the lattice designer, ↑ as seen by the design engineer, and how it looks in reality ր Andreas Streun, PSI 91 3. Transverse beam dynamics Betatron oscillations Betatron oscillations x′′ + kx = 0 constant focusing channel (e.g. long quadrupole, k = b2): Harmonic oscillator solutions: x(s) = xo cos √ ks + x′o sin with √ √ ks = a cos( ks + φo) x′o φo = arctan − √ kxo √ √ x (s) = −a k sin( ks + φo) and a = ′ s x2o + x′o √ k 2 Phase space plot / Poincaré plot: equidistant√observations spaced by ∆s Phase advance of betatron oscillation ∆φ = k∆s ellipse ascpect ratio given by k Andreas Streun, PSI √ =⇒ Transformation to circle: x′ → x′ / k 92 3. Transverse beam dynamics Variable focusing channel (beam transport line): Betatron oscillations x′′ + k(s)x = 0 high k variable k(s) fast oscillation p x(s) = A β(s) cos(φ(s) + φo) + [D(s)δ] Formalism ( A = Ao invariant betatron amplitude φo betatron phase =⇒ Particle properties δ = ∆p/p relative momentum deviation ( β(s) beta-function φ(s) betatron phase advance =⇒ Lattice properties D(s) dispersion function low k slow oscillation Andreas Streun, PSI 93 3. Transverse beam dynamics Goal: Description of the whole beam. p Particle i: xi(s) = Ai β(s) cos(φ(s) + φio) + [D(s)δi] Betatron oscillations (i = 1 . . . N ) Particle distributions: Initial Betatron phase φio: typically uniform Invariant amplitude Ai and momentum δi: any distribution (e.g. Gaussian). =⇒ statistical definition of beam size: q P p N Define rms (root mean square) beam size: σx = hx2i = N1 i=1 x2i p =⇒ σx = ǫβ(s) + [D(s)σδ ]2 ( because hcosi = 0, hcos2 i = 12 for uniformly distributed angles) p A2 with ǫ = h 2 i the beam emittance and σδ = hδ 2i the rms rel. momentum spread. =⇒ Decoupling: invariant beam parameters ǫ, σδ ⇐⇒ beam-independent lattice functions β(s), D(s) −→ redefine betatron amplitude: J := A2/2, so that ǫ = hJi =⇒ chapter 5. Andreas Streun, PSI 94 3. Transverse beam dynamics Betatron oscillations Twiss parameters Ansatz: harmonic oscillator with envelope function β(s) and variable phase φ(s): p x(s) = A β(s) cos(φ(s) + φo) p √ [ a → A β(s) ks → φ(s) ] → insert into DE, separate sin and cos terms → 2 DE for φ, β → solve for φ(s) → insert into β -DE: R R =⇒ βφ + β φ = 0 −→ φ(s) = ds phase equation β 1 ′2 1 ′′ 2 =⇒ β β − β + k(s) β = 1 beta equation 2 4 ′′ ′ ′ → insert β, β ′ , φ, φ′ into x(s), x′ (s) and eliminate sin and cos → βx′2 + 2αxx′ + γx2 = A2 [tilted] ellipse equation with the Twiss parameters: − 21 β ′ Beam envelope =⇒ ′′ α := p R(s) := A β(s) = maxφo (x(s)) R + k(s)R − Andreas Streun, PSI β A4 R3 =0 γ := 1+α2 β φ= R 1 β ds envelope equation 95 3. Transverse beam dynamics Betatron oscillations Twiss parameter transformation =⇒β(s), α(s), γ(s) βx′(s)2 + 2αx(s)x′(s) + γx(s)2 = A2 Transfermatrix: or inverse: ∀ s since A is constant. m12x′o m22x′o x x m11xo + = = M · ′ ′ x x x m x + 1 o 21 o ′ x x m22x1 − m12x1 −1 · = M = ′ x x′ x′ −m 21 x1 + m11 x1 o 1 → insert for so , s1 into ellipse equation, extract coefficients for β, α, γ and combine into vector → β α γ ! 1 = m211 −2m12m11 m212 −m11m21 m22m11 + m12m21 −m12m22 m221 −2m22m21 m222 Alternative writing: Andreas Streun, PSI β −α −α γ 1 = Mx ! β −α −α γ · β α γ MxT 0 ! o 96 3. Transverse beam dynamics Betatron oscillations Example: Drift space k = 0, −→ Mx = 1 s 0 1 β(s) = βo − 2sαo + s2γo α(s) = αo − sγo γ(s) = γo single particles: xi(s) = xio + s x′io p envelope: R(s) = A βo − 2sαo + s2γo 4 equivalent: solve k = 0 envelope equation R′′ = A3 R s 2 2 A → R(s) = Ro2 + 2sRo Ro′ + s2 Ro′2 + R o Gain: Description of the beam: • Transformation of all particles irrespective of individual initial conditions. • Decoupling of magnet structure (k(s) → β, α, γ) from beam properties (ǫ, σδ ). Andreas Streun, PSI 97 3. Transverse beam dynamics Betatron oscillations Normalized coordinates Particle in phase space moves on a tilted ellipse of area πA2: √ x(s) = A β cos(φ + φo) x′(s) = − √Aβ (sin(φ + φo) +α cos(φ + φo)) Transformation to a circle: ~x = x x′ √ β 0 A cos φo cos φ − sin φ · A sin φ = − √α − √1 · sin φ cos φ o β β {z } {z } | | | {z } R(φ) T χ ~o Normalized coordinates: χ ~ 1 = R(φ) χ ~ o, transformation = rotation in phase space. q √ β1 (cos ∆φ + αosin ∆φ) βoβ1sin ∆φ β o −1 M0→1 = T1R(∆φ)To = (α −α )cos ∆φ−(1+α α )sin ∆φ q β o o 1 1 o √ (cos ∆φ − α1sin ∆φ) β β β 1 o 1 Andreas Streun, PSI 98 3. Transverse beam dynamics Betatron oscillations Periodicity Circular lattice (0 = 1): One turn matrix with µ = ∆φo→o =: 2πQ, and Q the betatron tune: M= cos µ + αsin µ βsin µ −γsin µ cos µ − αsin µ symmetry point −→ cos µ βsin µ 1 − β sin µ cos µ m11 − λ m12 M =λ −→ m21 m22 − λ s Tr(M ) 2 Tr(M ) 2 0 = m11 m22 − m12 m21 − (m11 + m22 ) λ + λ = 0 −→ λ1/2 = ± −1 = | {z } | {z } 2 2 Stability condition: calculate eigenvalues of linear system =|M |=1 x x′ x x′ =0 e ±iµ =Tr(M ) with cos µ := Tr(M )/2 → stability requires real µ for oscillating (elliptic) solution. =⇒ Periodicity condition: | cos µ| < 1 with cos µ = 12 Tr(M ) otherwise no periodic solutions exists and β, α, γ are undefined. Gain: The complete transformation 0→1 is contained in the Twiss parameters α, β, γ at s0, s1 and the phase advance ∆φ0→1. Andreas Streun, PSI 99 3. Transverse beam dynamics Betatron oscillations Twiss parameters and the Hamiltonian H = 12 p2x + 21 k(s)x2 (k = b2) −→ x′ = px, p′x = −kx → x′′ = −kx √ √ √ x = 2J β cos(φ + φo), with 2J := A 2 Canonic transformation with generating function F (x, φ) = − 2xβ (tan φ + α) ′ proof: x = p = ∂F ∂x =− New Hamiltonian: H̃ = ′ φ = ∂ H̃ ∂J = 1 β √ 2J β J β (s) −→ φ = R (sin φ + α cos φ) J = − ∂F ∂φ = J → new equations of motion: 1 β ds H̃ J ′ = − ∂∂φ = 0 −→ J is invariant. (J; φ) are action-angle variables. 2J = betatron amplitude Gain: ⊲ Amplitude J proven to be an invariant. ⊲ Simple Hamiltonian → useful for perturbation studies (nonlinearities) Andreas Streun, PSI 100 3. Transverse beam dynamics Betatron oscillations Application: the FODO cell FODO = Focusing - space - Defocusing - space = repetition of the quadrupole doublet choose symmetry point (α = 0)and define r := L f 1 0 1 0 1 1 L 1 L · M = · · · 0 1 0 1 −2/f 1 1/f 1/f 1 ! 1 − 2r2 2L(1 − r) cos µ + α sin µ β sin µ = −γ sin µ cos µ − α sin µ −2r(1 + r)/f 1 − 2r2 0 1 = cos µ = m11+2 m22 = 1 − 2r2 −→ stability for 0 < |r| < 1 √ sin µ = 2r 1 − r2 q m12 1−r −→ β = sin = |f | µ 1+r α= m11 −m22 2 sin µ Andreas Streun, PSI =0→γ= 1+α2 β = 1 β 101 3. Transverse beam dynamics Betatron oscillations FODO cell beta functions horizontal and vertical beta functions in a FODO-cell. L/F = 0.06 → Qx = Qy = 0.02 L/F = 0.99 → Qx = Qy = 0.46 L/F = 0.5 → Qx = Qy = 0.17 L/F = −0.5 → Qx = Qy = 0.17 Andreas Streun, PSI 102 3. Transverse beam dynamics Andreas Streun, PSI Betatron oscillations 103 3. Transverse beam dynamics Imperfections Resonances Dipole error → kick on beam: R R By ds ∆x′ = b1ds = (Bρ ) → Increase of betatron amplitude if tune Qx near integer number → beam loss! (stability near half integer, alternating kicks + − + − . . . ) R ′ Quadrupole error: ∆x = x · b2ds −→ unstable if tune Q near half integer! Multipoles drive any resonance: AQx + BQy = C (A, B, C integers) Resonance order n = |A| + |B| B even / odd ←→ regular (bn ) / skew (an ) multipoles Tune diagram: Andreas Streun, PSI 1 2 3 4 Dipole Quadrupole Sextupole Octupole 104 3. Transverse beam dynamics Imperfections Orbit distortion Dipole kick ∆x′ and non-integer tune → perturbation of periodic orbit use normalized coordinates: √ ∆χ′ /2 ′ ′ 1 ∆χ = β ∆x −→ sin π − 2 2πQ = a : √ β ∆x′ Orbit amplitude a = 2 sin πQ Kick at location k, observation at location i −→ closed orbit equation: x 0 x + M = M i→k k→i x′ ∆x′ x′ i k i → use normalized coordinates (transformations are just rotations) → generalize to m kicks (superposition of linear solutions) m √ X βiβk xi = cos(φki) ∆x′k 2 sin πQ k=1 Andreas Streun, PSI φki = φi − φk + πQ φi − φk − πQ (i < k) (i > k) 105 3. Transverse beam dynamics Imperfections Orbit correction Orbit correction system: m corrector magnets (small dipoles) and n beam position monitors (BPM). Calculate (or measure) the (m × n) Response Matrix A: element Aki contains orbit at BPM i for single kick from corrector k: (Example for n = m = 72, Ref.: M.Böge, Orbit Feedback at SLS, Cern Accelerator School Brunnen 2003) Corrector settings for zero orbit obtained by {∆x′k } = −R−1 · {xi}, with vectors {xi} of n BPM orbit measurements, {∆x′k } of m corrector kicks. Andreas Streun, PSI 106 3. Transverse beam dynamics Imperfections Chromaticity Quadrupole: Length L Strength b2 = 1 d By (B ρ) d x Kicks on particle: ∆x′ = −b2Lx ∆y ′ = b2Ly (B ρ) := p = 3.3356 Tm · E [GeV] e (b2 > 0 → horiz.foc.) b2 Chromatic aberration: b2(δ) = ≈ b2 (1 − δ) (1 + δ) ∆p δ := p δ>0 δ=0 δ<0 Andreas Streun, PSI 107 3. Transverse beam dynamics Imperfections Impact of chromatic focussing errors on the lattice tunes: (Gradient error ∆b2 ds) × (one turn matrix M) = (new one turn matrix M̃) Gradient error due to chromatic aberration: ±∆b2 = ∓b2δ (hor./vert.) 1 0 cos 2π Q̃ β sin 2π Q̃ cos 2πQ β sin 2πQ × = ±b2δ ds 1 −γ sin 2πQ cos 2πQ −γ sin 2π Q̃ cos 2π Q̃ 1 2 Tr(M̃) = cos 2π Q̃ = cos 2π(Q + ∆Q) = cos 2πQ ± 21 b2δ β sin 2πQ ds ∆Q ≪ 1 −→ ∆Q = ∓ 41π b2δ β ds Chromaticity = variation of tune with momentum: 1 ∆Q ξ := =∓ δ 4π =⇒ Head tail instability −→ b2(s) β(s) ds C very low limit for stored current. =⇒ off-energy tune meets resonances Andreas Streun, PSI I −→ Low energy acceptance 108 3. Transverse beam dynamics Imperfections Chromaticity correction Sextupole: By (x) = 21 B ′′ x2 local gradient: By′ (x) = B ′′ x “Order” by momentum: x (δ) = Dδ Andreas Streun, PSI 109 3. Transverse beam dynamics Imperfections b2 = Quadrupole: 1 d By (B ρ) d x ∆x′ = −b2Lx ∆y ′ = b2Ly Chromatic aberrations: Quadrupole: Sextupole: •• =⇒ ⌣ =⇒ ⌢ ∞ Andreas Streun, PSI b3 = ∆x′ = −b3L(x2 − y 2) ∆y ′ = 2b3Lxy bn(δ) = bn/(1 + δ) ≈ bn(1 − δ) Sextupoles in dispersive regions: Kicks on a particle Sextupole: 2 1 1 d By 2 (B ρ) d x2 x → Dδ + x y → y (keep up to second order in products of x, y, δ ) : ∆y ′ = +b2Ly −[b2L] δ y ∆x′ = −b2Lx +[b2L] δ x ∆x′ = −[2b3LD] δ x −b3L(x2 − y 2) −b3LD2δ 2 ∆y ′ = +[2b3LD] δ y +2b3L xy ! Chromaticity correction for (2b3LD = b2L): I 1 ! ξx/y = ± 2b3(s)D(s) − b2(s) βx/y (s) ds = 0 4π C nonlinear kicks. . . → Chaos, restriction of dynamic acceptance 110 3. Transverse beam dynamics Imperfections Chromaticity correction in the SLS Horizontal betatron tune Qx vs. ∆p/p for one period (=1/3 of the SLS lattice) before →, and after →→ chromaticity correction. Motion in horizontal phase space: Linear oscillation before correction (no sextupoles). Andreas Streun, PSI Dynamic aperture breakdown due to sextupole non-linearity after straightforward correction. Partial restoration of dynamic aperture after careful distribution of sextupoles. 111 4. Longitudinal dynamics ⊲ Synchrotron oscillations Momentum compaction. Phase stability. Synchrotron tune. ⊲ Longitudinal acceptance The bucket. Phase acceptance. Momentum acceptance. Andreas Streun, PSI 112 4. Longitudinal dynamics Synchrotron oscillations Synchrotron oscillations Circular machines (synchrotrons and storage rings): ⊲ time dependant energy gain in RF cavity ⊲ energy dependant time of recirculation =⇒ Synchrotron oscillation of energy vs. time Tune = number of oscillations per recirculation: synchrotron tune Qs, betatron tunes Qx, Qy Synchrotrons: Qs ≈ 10−4 . . . 10−2 ≪ Qx,y ≈ 1 . . . 100 (but e.g. microtron: Qs > Qx,y !) (t) =⇒ E(t), resp. δ(t) = ∆ppo(t) = β12 ∆E Eo treated as constant for betatron oscillations (adiabatic approximation) Andreas Streun, PSI 113 4. Longitudinal dynamics Synchrotron oscillations Momentum compaction and transition Time of flight T = C (δ ) cβ (δ ) , C = lattice circumference, δ = ∆p po . dT ∂T dC ∂T dβ 1 dC Co dβ = + = − 2 dδ ∂C dδ ∂β dδ cβo dδ cβo dδ dC dδ H Dispersion: x(s) = D(s) · δ → path length C(δ) = (ρo + Dδ) dφ Dipole magnets: dφ = ds/ρo H 1 dC dδ o = α Co with α := Co dβ dδ β=√ −→ C(δ) = Co + D ρo ds · δ βγ 1+(βγ )2 o Andreas Streun, PSI D ρo ds the momentum compaction factor. p = mocβγ = po(1 + δ) − 1 / 2 dβ −→ dδ = β = 1 + [βoγo (1 + δ)]−2 =⇒ H Co dT = dδ cβo α− 1 γo2 βo γo2 −→ ∆T = Toηδ with η := α − 1 γo2 114 4. Longitudinal dynamics Synchrotron oscillations Competitive effects: α −1/γo2 −→ high momentum particles have longer path due to dispersion −→ high velocity particles are faster Electron synchrotrons: γo ≫ 1, β ≈ 1 −→ η = α Proton synchrotrons: √ isochronous (i.e. η = 0) at transition energy Etr = moc / α 2 . . . use RF phase instead of time: ψ = 2π τT rf with τrf = ∆ψ = 2πhη δ or ∆ψ = 1 frf = To h, h ∈ N the harmonic number and To = Co cβo . 2πh ∆E η Eo βo2 . . . use path length (longitudinal driftspace) instead of time: ∆s = −βoc∆T = −Coηδ Andreas Streun, PSI 115 4. Longitudinal dynamics Synchrotron oscillations Phase stability Energy change of particle at phase ψ for one turn: ∆tE(ψ) = qV sin ψ − U (E) Note: ∆t E = E (t + To ) − E (t), but ∆E = E − Eo . Eo = reference particle’s energy V = peak voltage of RF cavity. U (E) = [energy dependant] energy loss per turn = Uo + U ′∆E with U ′ = dU/dE (e.g. synchrotron radiation: U ∼ E 4!). Synchronous phase: ∆tE = 0 = qV sin ψs − Uo −→ sin ψs = Uo qV Use phase shift relative to synchronous particle ∆ψ = ψ − ψs and relative momentum deviation δ = 1 ∆E βo2 Eo Synchrotron oscillation is ”slow” → δ̇ ≈ ∆t δ To = change per turn. =⇒ longitudinal non-linear equations of motion in δ and ∆ψ: δ̇ = qV βo2 Eo To · (sin(ψs + ∆ψ) − sin ψs) − U ′ Tδo ֒→ ∆ψ = 2πhη · δ Andreas Streun, PSI −→ ˙ = (∆ψ) 2πhη To δ 116 4. Longitudinal dynamics Synchrotron oscillations Synchrotron Tune ∆ψ ≪ 1 −→ δ̇ = qV βo2 Eo To cos ψs · ∆ψ − U ′ Tδo −→ d/dt again and introduce (∆˙ψ ) −→ damped oscillator equation: δ̈ + 2Λδ̇ + Ω2δ = 0 with 2Λ = ′ U To q and Ω = βo1To −(η cos ψs) 2πhqV Eo Solution δ(t) = δoeωt with ω 2 + 2Λω + Ω2 = 0 ω = −Λ ± √ Λ2 − Ω2 ≈ −Λ + iΩ for Λ ≪ Ω Stability requires real Ω η<0→ η>0→ −90◦ ◦ 90 Synchrotron tune Qs = Andreas Streun, PSI −→ η cos ψs < 0 : 90◦ ◦ < ψs < < ψs < 270 synchrotron frequency revolution frequency = √ below transition, i.e. γ < α above transition (electrons always) Ω/2π 1/To = 1 βo q −(η cos ψs) 2hqV πEo 117 4. Longitudinal dynamics Longitudinal acceptance The bucket back to full non-linear equations of synchrotron motion: δ̇ = qV (sin(ψs + ∆ψ) − sin ψs) 2 βoEoTo 2δ = To ˙ (∆ψ) πhη [U ′ ≈ 0] d δ 2 = 2δ δ̇ and d cos(ψ + ∆ψ ) = − sin(ψ + ∆ψ ) (∆˙ψ ) and integrate → → cross-wise multiplication, use dt s s dt δ2 + qV (cos(ψs + ∆ψ) + sin ψs ∆ψ) = constant := H 2 | {z } πβoEohη :=W (∆φ) δ 2 ∼ p2 = kinetic energy, W = potential, H = Hamiltonian of the oscillation: harmonic for small amplitudes: ∆ψ ≪ 1 −→ cos(ψs + ∆ψ ) ≈ cos ψs − sin ψs · ∆ψ − 12 cos ψs (∆ψ )2 −→ δ 2 − k · (∆ψ )2 = H − 2k (k = const.) −→ ellipses in (∆ψ, δ ) phase space for η cos ψs < 0 Potential W (∆ψ ) for acceleration above transition → η > 0 and 90◦ < ψs < 180◦ −→ sin ψs > 0, cos ψs < 0. Formation of 2π-periodic regions of stable synchrotron oscillations, called buckets. Andreas Streun, PSI 118 4. Longitudinal dynamics Longitudinal acceptance Phase acceptance Separatrix = curve in phase space separating stable from unstable regions. Phase acceptance = interval of stable phase [∆ψ1, ∆ψ2] for δ = 0: ! 1. one limit given by bucket wall: ddW −→ sin(ψs + ∆ψ) = sin ψs ∆ψ = 0 −→ ∆ψo = 0 (bucket bottom) and (since sin x = sin(±π − x)), ∆ψ1 = ±π − 2ψs 2. other limit given by separatrix equipotential: W (∆ψ2) = W (∆ψ1) −→ solve numerically to get ∆ψ2. (for small buckets ∆ψ2 ≈ − 21 ∆ψ1). =⇒ Phase acceptance above and below transition energy: • ψs → 90◦: maximum acceleration: ∆tE → qV minimum acceptance: ∆ψ1,2 → 0 • ψs = 180◦ or ψs = 0◦ no acceleration: ∆tE = 0 full acceptance: ∆ψ1,2 = ±180◦ Andreas Streun, PSI 119 4. Longitudinal dynamics Longitudinal acceptance Momentum acceptance Insert separatrix point (∆ψ1, 0) into the Hamiltonian equation to get H. −→ Separatrix equation: δ2 + ∆ψ = 0 qV [cos(ψs + ∆ψ) + sin ψs · (∆ψ + 2ψs − π) + cos ψs] = 0 2 πβoEohη −→ momentum acceptance (or energy acceptance) of the machine: 2 δac = qV [2 cos ψs + (2ψs − π) sin ψs] 2 πβoEohη for electrons use Uo = V sin ψs, η = α and βo = 1: h i π 2U o 2 cot ψs + ψs − = δac πEohα 2 Andreas Streun, PSI 120 5. Emittance ⊲ Liouville’s theorem Hamiltonian system. The Vlasov equation. Invariance of phase space volume. Symplecticity. ⊲ Excursion into chaos Non integrable systems. KAM-tori and resonance islands. ⊲ Transverse emittance Geometric emittance. Normalized emittance. ⊲ Liouville applications Acceleration. Chromaticity and slice emittance. Space charge. Synchrotron radiation. ⊲ Particle distributions Statistical emittance definition. The Gaussian distribution. Energy spread and bunch length. Andreas Streun, PSI 121 Emittance Introduction Complete beam description Transverse and longitudinal dynamics: → propagate single particle with amplitude A in 6-d-phase space. Choose ”representative” amplitude A to describe the whole beam: √ ⊲ homogeneous current density, sharp edge: A√ β = xmax (envelope) ⊲ Gaussian distributed current density: A β = σx (r.m.s. size) "bones" magnets and RF structures → beta functions, tunes and transfer matrices, independant of individual coordinates and particle distributions. "flesh" 6-d-phase space volume of the beam, independant of the magnets and RF structures. "body" complete beam description Andreas Streun, PSI 122 Emittance Liouville’s theorem Liouville's theorem A foundation of accelerator physics and celestial mechanics ”The beam’s phase space volume is constant.” Hamiltonian system: 1. no velocity dependant forces ~ except Lorentz force, since F~ ⊥ ~v (~ p → p~ − q A) no dissipation (friction) 2. no individual forces on particles ~ all forces derived from potentials (e.g. Φ, A) no scattering (between particles or with residual gas atoms) 3. no (or very slow) time dependance, ∂H/∂t = 0 =⇒ Hamiltonian equations: q̇i = ∂H/∂pi, ṗi = −∂H/∂qi p, q canonical positions and momenta, i = 1 . . . 3N , N number of particles. Andreas Streun, PSI 123 Emittance Liouville’s theorem Description of beam status: single particle status is 1 point in 6-d-space is N points in 6-d-space N particle status or 1 point in 6N -d-space } equivalent, if particles do not interact (i.e. each particle moves independant from the others). P3N ˆ ˆ~ Status vector in 6N -d-space: ~r = i=1 qi~qi + pip i P3N ˆ ˆ~ Evolution of status: velocity ~v = i=1 q̇i~qi + ṗip i If all forces are derived from potentials, there exists a velocity field guiding evolution of all possible vectors in 6N -d-space: Divergence 3N 3N X X ∂ ∂H ∂ ∂ ∂H ∂ q̇i + ṗi = − =0 div ~v = ∂q ∂p ∂q ∂p ∂p ∂q i i i i i i i=1 i=1 −→ Property of an incompressible liquid Andreas Streun, PSI 124 Emittance Liouville’s theorem Vlasov equation (continuity equation from fluid dynamics, ̺ density): ∂̺ ∂̺ 0= + div(̺~v ) = + ~v grad̺ +̺ div~v ∂t ∂t {z } | =d̺/dt No divergence =⇒ constant [phase space] density: ⊲ all density changes are due to flux, no sources or drains ⊲ causality (same cause → same effect): trajectories never cross or merge −→ this result obtained in 6N -d-space is valid in 6-d-space too −→ The 6-d-volume enclosing N particles in phase space is invariant. Accelerators: decoupling of sub-spaces: horizontal (x, px), vertical (y, py ), longitudinal (∆ψ, δ) Emittance = invariant 2-d phase space area Andreas Streun, PSI 125 Emittance Liouville’s theorem Symplecticity Linear beam transformation with transfermatrix: ~x1 = M · ~xo symplectic matrix, i.e |M | = 1 2-d phase space vectors ~x1, ~x2 enclose area a = 21 |~x1 × ~x2| Linear transformation ~x = M~xo −→ Area a = 12 |(M~x1o) × (M~x2o)| = 12 |M | |~x1o × ~x2o| = |M |ao General transformation with non-linear map: ~x1 = M(~xo) dM Symplectic map: local Jacobian d~x = 1 Filamentation Area a is conserved, but area ã to accept the beam is increased. → irreversibility! Andreas Streun, PSI 126 Emittance Liouville’s theorem Example: symplectic mapping Nonlinear Hamiltonian: (s) p2 H(x, p; s) = 2 − Fm cos(mx) Equations of motion: x′ = ∂H ∂p = p p′ = − ∂H ∂x = −F (s) sin(mx) Assume: cell length d, F 6= 0 in small region ∆s at s = d/2 One-turn mapping: x ← x + d2 p p ← p − F ∆s sin(mx) x ← x + d2 p ∂ ∆x; ∆p Symplectic: ∂ x; p = 1 → prove! Test (10 recursions): initial / final area: Filamentation, but conservation of area. (area measurements by IDL function poly area: 1.41107e-06 1.41089e-06 ) Andreas Streun, PSI 127 Emittance Chaos Excursion: Chaos Solution of equations of motions = canonic transformation of Hamiltonian to harmonic oscillator (amplitude J, frequency ω) −→ elliptic orbits in 2-d space, resp. tori in higher dimensional spaces. Hamiltonian with non-linear perturbation: Siegel’s theorem: All tori to rational frequencies (ω = r/s; r, s ∈ N ) are unstable (non-integrable, i.e. no solution/transformation can be found). KAM (Kolmogorff-Arnold-Moser) theorem: Tori are deformed, but stable, if • there is a twist ∂ω/∂J 6= 0 (amplitude dependant frequency), • the frequency is “sufficiently irrational”, ω − rs > sab ∀s; a, b > 0, • and the perturbation is “small”. Moser’s twist theorem Any KAM orbit (projection of torus to 2-d space → Poincaré plot) can be transformed into a circle, where each point is fixpoint. Poincaré and Birkhoff’s fixpoint theorem Unstable orbits for ω = r/s split into s elliptic and s hyperbolic fixpoints −→ resonances appear as “island chains”. Andreas Streun, PSI 128 Emittance Chaos Inside the islands (elliptic fixpoints): Mapping (local Jacobian) has imaginary eigenvalues: |J − λ| = 0 → λ = e±iφ → harmonic oscillations. Outside the islands (hyperbolic fixpoints): real eigenvalues: λ1 = a, λ2 = 1/a Filamentation of phase space areas due to area conservation and rapid increase of enclosing curve length. −→ inflation of constraints ! Deterministic Chaos: weak causality still valid, same causes −→ same effects. strong causality violated, similar causes −→ × similar effects. Islands become new centers of [modulo-s] motion → self similarity G.Eilenberger, Reguläres und chaotisches Verhalten Hamiltonscher Systeme, in: 14.Ferienkurs Nichtlineare Dynamik in kondensierter Materie, KFA Jülich, 1983 Andreas Streun, PSI 129 Emittance Transverse emittances Transverse emittances Linear motion −→ beam ellipse in 2-d-space Ellipse area: a = πǫ. Geometric emittance ǫ in (x, x′)-plane: Define emittance by a contour confining some fraction of particles depending on distribution (e.g. homogenous, Gaussian, etc.) Emittance units: [rad·]m or mm·mrad or nm[·rad] Alternative emittance definition: a = ǫ, unit π mm·mrad Normalized emittance ǭ ≈ hβγiǫ Andreas Streun, PSI ( → light source community) ( → linac community) ǭ measured in (x, px) plane in units of moc mm·mrad if x′ ≈ px/ps (paraxial approximation) and |p − hpi| ≪ 1 (monochromatic approximation) 130 Emittance Liouville applications Emittance invariance In which cases is emittance an invariant (i.e. Liouville theorem holds)? ⊲ ⊲ ⊲ ⊲ ⊲ Non-linearity −→ ok Acceleration Chromaticity Space charge Synchrotron radiation (see above) Acceleration ∆ps > 0, ∆px = 0 −→ ∆x′ ≈ ∆px ps <0 =⇒ geometric emittance ǫ in {x, x′} shrinks: ǫ ∼ 1/ps. =⇒ normalized emittance ǭ in {x, px} is invariant. adiabatic damping or pseudo-damping: no violation of Liouville’s theorem. Andreas Streun, PSI 131 Emittance Liouville applications Chromaticity and slice emittance Example: chromatic aberration of a quadrupole Beam ellipses to different momenta δ transform differently. Increase of projected emittance enclosing all ellipses in (x, x′)-space. Volume in (x, x′, δ)-space: torsion but no increase: slice emittance ǫ(δ) constant. =⇒ no violation of Liouville’s theorem! −→ important for free electron lasers, performance depends on slice emittance. Andreas Streun, PSI 132 Emittance Liouville applications Space charge Cylindrical, homogenous, unbunched beam R linear force Fsc ∼ r, potential Φsc = Er dr o ·r =0 add to linear transformation: r′′ + k − 2mqjµ 3 o c(βγ ) linear defocusing – but check for convergence: j = =⇒ Liouville’s theorem valid. I 2 πrmax ! Bunched beam with non-homogeneous current density Potential Φsc exists, but non-linear radial and longitudinal forces cause filamentation and coupling. Increase of projected and slice emittances. =⇒ Liouville’s theorem still valid. Coulomb scattering, e.g. − intra-beam scattering in low energy synchrotrons, − beam-beam scattering in circular colliders − scattering on residual gas atoms Stochastic events, acting individually on each particle. True emittance blow-up. =⇒ Liouville’s theorem violated. Andreas Streun, PSI 133 Emittance Liouville applications Synchrotron radiation 1. Electron emits radiation along its momentum −→ both px and ps decrease. 2. RF cavity supplements ps and does not change px. Damping of transverse momentum px = pxoe−iΛt Decrease (cooling) of normalized emittance ǭ in (x, px)-space. =⇒ Liouville’s theorem violated. Quantized radiation → individual recoil and excitation of transverse oscillations. Increase (heating) of emittance due to stochastic events. =⇒ Liouville’s theorem violated again. Electron storage rings: emittances given by cooling/heating equilibrium. (independant of injected beam properties, damping time < 1 s). Slow process compared to betatron and synchrotron oscillations, e.g. SLS: Λx,y ≈ 100 Hz Betatron frequency Qx,y /To ≈ 100 MHz Synchrotron frequency Qs /To ≈ 5 kHz Λs ≈ 200 Hz =⇒ Liouville violation due to radiation can be neglected in many calculations. Andreas Streun, PSI 134 Emittance Distributions Statistical emittance definition Particle distribution ̺(x, x′) −→ r.m.s. beam size and divergence Reference orbit (origin): hxi = 0, hx′i = 0. RR 2 x ̺(x, x′) dx dx′ 2 2 σx = hx i = R R ̺(x, x′) dx dx′ σx2 ′ ′2 = hx i, ′ (σx) = hxx′ i σx √ √ Ellipse parameters: σx = ǫ β, 2 2 βγ − α = 1 −→ ǫ = Normalized coordinates σx2 (σx2 ′ ′ √ √ σx′ = ǫ γ, ′ (σx) = √ α√ ǫ − β p − ((σx) ) ) =⇒ ǫ = hx2ihx′2i − hxx′i2 (χ, χ ): ′ 2 x= √ β χ, x′ = − √αβ χ − √1β χ′ ǫ2 = hχ2ihχ′2i, since hχχ′i = 0 (uncorrelated) by transformation √ 2 2 ′2 2 hχ i = hχ i = σχ = σχ′ = ǫ → circle with radius ǫ. Andreas Streun, PSI 135 Emittance Distributions Emittance is average betatron amplitude for any particle distribution isotropic in phase angle. ǫ = hJi Individual particle betatron amplitude (2J) and initial phase φo: p d x(s) = 2J β(s) cos(φ(s) + φo) −→ ds φ′ = β1 β ′ = −2α q x′(s) = − β2(Js) (sin(φ(s) + φo) + α(s) cos(φ(s) + φo)) a) easy wasy to prove: transformation to action-angle variables: √ √ ∂χ∂χ′ ′ ′ ∂x∂x χ = 2J cos φ, χ = 2J sin φ ∂J∂φ = 1, ∂χ∂χ′ = 1 hχ2i ǫ= = hχ′2i RR cos2 φ 2J ̺(J, φ) dJ dφ sin2 φ RR ̺(J, φ) dJ dφ b) lengthy way to prove: ǫ = Andreas Streun, PSI p hx2ihx′2i − hxx′i2 ̺ 6= ̺(φ) −→ R dφ R J ̺(J) dJ R = hJi ̺(J) dJ etc. . . 136 Emittance Distributions Gaussian distribution • natural in many cases → Maxwell distribution of momenta at thermionic cathode → synchrotron radiation equilibrium • fair approximation in other cases e.g. parabolic beam profile with halo • convenient to handle (r.m.s. quantities) 2 ′2 1 1 − χ2ǫ − χ2ǫ ·√ √ e ̺(χ, χ ) = √ √ e 2π ǫ 2π ǫ ′ RR ̺(χ, χ′) dχ dχ′ = 1 1 − γx2+2αxx′+βx′2 2ǫ e ̺(x, x ) = 2π ǫ ′ Andreas Streun, PSI 137 Emittance Distributions ̺(x) = Z +∞ −∞ 2 − x2 1 ′ ′ ̺(x, x ) dx = √ e 2σx , 2π σx 1 −J ̺(J, φ) = e ǫ 2πǫ −→ with σx = p ǫβ − Jǫ ̺(J) = e Particles contained in distributions: A(x) = Z +x ̺(x) dx = erf −x B(J) = Z 0 J x √ 2 J ̺(J) dJ = 1 − e− ǫ x/σx 2J/ǫ A B 1 2 3 1 4 9 0.683 0.956 0.997 0.393 0.865 0.989 Andreas Streun, PSI 138 Emittance Distributions Energy spread and bunchlength Longitudinal emittance ǫs may be defined in (∆ψ, δ)-space, but uncommon: Synchrotrons: Qs ≪ 1 → αs ≈ 0 → little coupling ∆ψ ↔ δ → Use [relative] r.m.s. energy/momentum spread σδ2 = hδ 2i. → Use spatial or temporal r.m.s. bunchlength σs2 = h(∆s)2i or σt2 = h(∆t)2i. ψ (∆t = ∆ 2π τrf , ∆s = βc∆t). Electron storage rings: σδ given by synchrotron radiation equilibrium σs follows from RF and magnet parameters (Vrf , α, C etc.) Peak current Iˆ = ̺(∆t = 0) Gaussian beam: ̺(∆t) = − √Q e 2πσt (∆t)2 2σt2 → Iˆ = √Q 2π σ t Bunch charge = average current × recirculation time. R Q = ̺(∆t) d(∆t) = I · To Andreas Streun, PSI Bunchlength measurement at SLS 139 6. Synchrotron Radiation ⊲ Synchrotron radiation Power. Collimation. Time structure. Spectrum. Brightness. ⊲ Radiation equilibrium Radiation damping. Quantum excitation. The equilibrium. ⊲ Light Sources Example: SLS. Minimum emittance. Free electron laser. Andreas Streun, PSI 140 Lorentz transformation Transformation from lab sytem K to system K ′ moving at speed βc in z-direction: x′ y′ z′ ′ 1 0 ML = 0 0 0 0 1 0 0 γ 0 −βγ px py = M · L p z E/c E /c x y = M · L z ct ct p′x p′y p′z ′ 0 0 −βγ γ ML−1 1 0 = 0 0 0 0 1 0 0 γ 0 +βγ 0 0 +βγ γ Moving particle: z ′ = 0 → z = βγct′ and ct = γct′ → lab system: z = βct 4-vectors: space-time S̃ = (x, y, z, ict) and momentum-energy P̃ = (px, py , pz , iE/c) p Length of 4-vectors is Lorentz-invariant. |P̃ | = P̃ · P̃ = imoc Andreas Streun, PSI 141 6. Synchrotron radiation Radiation properties Synchrotron radiation power Radiation of an accelerated charged particle (Hertz dipole characteristics): P = e moc2 2 c 6πεo d2 P Angular distribution dφ dθ Maximum power ⊥ to acceleration d~ p dt 2 [SI] ∼ sin2 θ Relativistic invariant formulation using 4-momentum P̃ = [~ p, iE/c] 4-D scalar product: d~ p 2 dt consider −→ P̃a · P̃b = p ~a · p ~b − Ea Eb /c2 dP̃ dt′ d~ p/dt′ k p ~ d~ p/dt′ ⊥ p ~ Andreas Streun, PSI !2 = −→ P̃ 2 = −mo c dE 2 1 d~ p 2 − 2 dt′ c dt′ linear acceleration circular acceleration with ′ t = 1 t γ time in moving system. → linac → synchrotron 142 6. Synchrotron radiation Radiation properties Linear acceleration Radiation cannot separate from the Coulomb field. E 2 = (mo c2 )2 + (pc)2 → dE′ = β dp′ (1 − β 2 ) = 1/γ 2 dt dt 2 2 d~ p dP̃ ~ 2 (electric field) = (e E) = ′ dt dt ~ = 25 MV/m −→ P = 10−16 W Example: acceleration with gradient |E| per 1 m linac: electron energy increase 25 MeV, radiation loss 2 µeV → negligible! Circular acceleration Radiation separates fast from the Coulomb field. d~ p p = γ d~ dt dt′ 2 mv 2 = pv = βpc = β E centrifugal acceleration dp = R R R R dt 2 2 βγE dP̃ E e2 c ′ dt R 6πεo mo c2 dE/dt′ = 0 −→ = −→ P = Uo [keV] = β2 R2 [SI] 2πR only in bending magnets) c (radiation 4 e e (E [GeV])4 33 10 R [m] 3εo moc2 Energy loss per turn Uo = P β ≈ 1 −→ 4 | {z 88.5 } Example: SLS at 2.4 GeV, R = 5.7 m −→ Uo = 512 keV per electron. max. current I = 400 mA → P = Uo · I = 205 kW! → supplied by RF. Andreas Streun, PSI 143 6. Synchrotron radiation Radiation properties Collimation Acceleration in x-direction −→ max. emission in y and z directions. Assume photon (β = 1!) momentum in y direction: Lorentz transformation to lab system: Collimation angle tan Θ = py pz = py = p′y p′y = pz = E′ c , pz = 0 E′ γc = γp′y 1 γ Example: ESRF at 6 GeV −→ Θ = 85 µrad. Beam spot 1 cm diameter in 60 m distance. ESRF (European Synchrotron Radiation Facility) (Grenoble, France) Andreas Streun, PSI −→ 144 6. Synchrotron radiation Radiation properties Time structure and photon energy Collimation → Observation from narrow sector (small depth of field) pulse duration = time delay (electron − photon) 2RΘ 2R sin Θ ∆t = − cβ c −→ sin Θ ≈ Θ − Θ3 , 6 =⇒ typical frequency νtyp = 1 q β = 1 ∆t 1 1−1/γ 2 ≈ 1 1−1/(2γ 2 ) ≈ 1 + 12 2γ −→ and energy Ẽtyp = hνtyp = 4R ∆t = 3cγ 3 3hc 3 4R γ . Example: ESRF at 6 GeV, R = 23 m −→ Ẽtyp = 65 keV – like X-ray tube Andreas Streun, PSI 145 6. Synchrotron radiation Radiation properties Radiation spectrum dP dω = P ωc S ω ωc (Ẽ = h̄ω) Define critical energy (frequency) Ẽc (ωc) : Z 0 ωc dP ! dω = dω Z Ẽc = h̄ωc = ∞ ωc 1 π dP dω dω Ẽtyp (figure from: H.Wiedemann,Particle accelerator physics 2) 2 −→ use BR = p/e −→ 3 e 3hc 2 Ẽc [keV] = 1015 (B [T] E [GeV]) 4πe moc2 | {z } 0.665 Andreas Streun, PSI 146 6. Synchrotron radiation Radiation properties Brightness and Undulators Brightness B = 6-d phase space photon density = spatial and angular flux density [B] = B∼ photons s mm2 mrad2 0.1% BW 1 ǫ x ǫy BW = bandwidth ∆Ẽ Ẽ (usually 0.1%) −→ Light sources require low transverse emittances. Example SLS ǫx = 5 · 10−9 rad m, ǫy ≈ 5 . . . 10 · 10−12 rad m −→ source size σx = 45 . . . 160 µm, σy = 2 . . . 8 µm (for different locations) Undulator magnet → coherent superposition of radiation → line spectrum → very high brightness Andreas Streun, PSI 147 6. Synchrotron radiation Radiation properties SLS brightness Bending magnet brightness in comparison to light bulb, sun and X-ray tube Andreas Streun, PSI Undulator brightness in comparison to bending magnet brightness 148 6. Synchrotron radiation Radiation equilibrium Equilibrium beam parameters References: M. Sands, The physics of electron storage rings, SLAC-report SLAC-121, 1970 corresponding chapters in books by K.Wille, S.Y.Lee and H.Wiedemann 1. Radiation damping Photon emission ∆px < 0 ∆py < 0 ∆ps < 0 Acceleration ∆px = 0 ∆py = 0 ∆ps > 0 ∆p ∼ p −→ exponential decay: u = uoe−t/τu pu = puoe−t/τu u = x; y; ∆s ∂B Calculate dU dδ , include dispersive orbits x = Dδ and magnetic field in gradient bends By (x) = Byo + ∂x x. Simple scaling U ∼ E 4 is only valid on axis! =⇒ Damping times τu = 2UToJEo o u u = x; y; s Damping partition numbers (for a flat lattice, i.e. D = Dx, Dy = 0) H hD(h2 − 2b2) ds C H Jx = 1 − D Jy = 1 Js = 2 + D with D = 2 ds h C By (0) ∂By 1 = orbit curvature, b = h = b1 = (Bρ 2 ) (Bρ) ∂x = quadrupole component. o Andreas Streun, PSI 149 6. Synchrotron radiation Radiation equilibrium Stability (i.e all Ju > 0) for −2 < D < 1. P Ju = 4 (Robinson theorem). → separate function lattice: bending magnets are pure dipoles (b2 = 0) → D ≈ 1 → combined function lattice: b2 < 0 (vertical focusing gradient) → D < 1, Jx > 1 2. Quantum excitation Photon recoil −→ stochastic excitation of synchrotron and betatron oscillations Calculation: Growth rate hδ˙2 i ∼ Ṅ hẼ 2 i = number of photons per turn × variance of photon energy longitudinal: ”noise” on energy −→ increase of beam energy spread. horizontal: Betatron oscillation around dispersive orbit corresponding to changed energy. Amplitude of oscillation: −1 Dδ ′2 ′ 2 2 a = T = (βD + 2αDD + γD ) ·δ ′ Dδ | {z } H H = dispersion’s emittance or lattice invariant. vertical: no excitation since emission k p~ and py → 0 due to radiation damping. Andreas Streun, PSI 150 6. Synchrotron radiation Radiation equilibrium 3. Equilibrium Radiation damping rate = quantum excitation growth rate =⇒ energy spread and bunch length σδ2 3 55 h̄c 2 h|h| i √ = γ 2 moc hh2i 32 3 | {z } σs2 = − αCEoλrf tan ψs · σδ2 2πUo Cq =3.84·10−13 m Bunch length follows from σδ through synchrotron oscillation: One turn longitudinal drift ∆s = αCδ, → ∆δs = αC = m12 -element of longitudinal transfer matrix in (∆s, δ )-space. m12 = βs sin 2πQs , Qs synchrotron tune and βs longitudinal ”beta function”. sin 2πQs ≈ 2πQs . Qs ≪ 1 −→ αs ≈ 0, γs = β1 ; s q √ √ ǫs αC σ . Longitudinal phase ellipse parameters: σδ = ǫs γs ≈ , σ = ǫs βs −→ σs = βs σδ = 2πQ s δ β s s =⇒ [natural] horizontal emittance ǫxo h|h|3 Hi = Cq γ hh2i Jx 2 vertical emittance: flat lattice, H = 0 everywhere → ǫyo ≈ 0 (h = 0 outside bending magnets) (direct recoil) misalignments (e.g. quadrupole rotation error, sextupole position errors) −→ emittance coupling Andreas Streun, PSI g := ǫy ǫx ≪1 −→ ǫx = ǫxo 1+g ǫy = g ǫxo 1+g 151 6. Synchrotron radiation Radiation equilibrium Swiss Light Source SLS Andreas Streun, PSI 152 6. Synchrotron radiation Light Sources Beam size in the SLS ↓ Beta functions and dispersions of the SLS storage ring: Zoom in on one of the bending magnets −→ Bending magnet center: βx = 0.45 m, βy = 14.8 m, D = 4 cm Natural emittance ǫxo = 5.5 nm rad, g = 0.1 % −→ ǫx = 5.5 nm rad ǫy = 5.5 pm rad Beam sizes (r.m.s energy spread σδ = 9 · 10−4 ): p p σy = ǫy βy = 9µm σx = ǫx βx + (Dσδ )2 = 61 µm Measurement: beam image from X-ray pinhole camera =⇒ Pinhole resolution (blur) 13 µm, to be subtracted quadratically p → measured σx = p (64.6 µm)2 − (13 µm)2 = 63 µm → measured σy = (15.9 µm)2 − (13 µm)2 = 9 µm Andreas Streun, PSI 153 6. Synchrotron radiation Light Sources Minimum emittance Emittance in isomagnetic lattice (i.e. same h = 1/ρ for all bends): 2 hHimag ǫxo [nm·rad] = 1470 (E [GeV]) Minimum emittance: ǫxo ρJx ! dhH(αxc, βxc, Dc, Dc′ )imag = 0 (E[GeV])2 Φ3F √ [nm·rad] = 1470 Jx 12 15 −→ Φ [rad] magnet deflection angle ≪ 1 =⇒ Light sources have many small bending magnets: ǫ ∼ Φ3, require sharp horizontal focus in bending magnets, βxc F =1 = 2√115 L Dc = Andreas Streun, PSI 2 1 24ρ L F =3 q 3 sf = 38 L βxf = 320 L operate usually at ǫ ≈ 3 . . . 5 × ǫmin . 154 6. Synchrotron radiation Light Sources Free Electron Laser Undulator radiation travels with beam, acts like accelerating RF field. =⇒ microbunching : bucket formation at radiation wavelength: ⊲ coherent radiation: bunch < wavelength → radiates like one super-particle. Radiated power: incoherent P ∼ N e2 coherent: P ∼ (N e)2 ! ⊲ self amplification: exponential increase of power with path length P ∼ es/Lg . Lg =gain length Power saturation at ≈ 22 Lg . Peak brightness of FELs =⇒ compared to storage ring undulators Andreas Streun, PSI 155 6. Synchrotron radiation Light Sources FEL schemes Oscillator not for X-rays (no mirrors available) SASE (Self Amplified Spontaneous Emission) start-up from noise → unstable Seeded FEL microbunching initialization by external laser pictures taken from: S. Werin, Tutorial on FEL, http://cas.web.cern.ch/cas/BRUNNEN/Presentations/PDF/tutorial-on-fel-011005.pdf Andreas Streun, PSI 156 6. Synchrotron radiation Wavelength λ ∼ Light Sources λu = undulator period [∼ cm] λu 2γ 2 ◦ λ = radiated wavelength [∼A] 1 √ Gain Length Lg ∼ 3 B u | {z λu} | undulator Diffraction limit: ǫ < λ 4π 4 → E ≈ 2 . . . 10 GeV 13 E ǫ → high peak current Iˆ > 1 kA! σs < 1 mm ˆ I{z } beam −→ ǫ ∼ 10−11 rad m σs, ǫx out of reach for storage rings −→ use linac: ǫ ∼ 1 E by pseudo-damping → Low emittance electron source developments (laser RF, nano field emitter etc.) DESY X-FEL pilot project FLASH (Free electron LASer at Hamburg) Andreas Streun, PSI 157 6. Synchrotron radiation Light Sources SwissFEL at Andreas Streun, PSI 158 7. Luminosity ⊲ Luminosity Gaussian beams. Hourglass effect. Space charge limit. Luminosity optimization. Tune spread. Beam-beam limit. Beam separation: Crab crossing and crab-waist. Beam disruption Andreas Streun, PSI 159 7. Luminosity Gaussian distribution Luminosity with Gaussian beams Luminosity = particles/time × particle/area L= N+ T − × NA∗ (A∗ common interaction area) Luminosity = 4-d overlap of particle distributions ̺± L = fc Z Z Z Z (β = 1): +∞ −∞ ̺+(x, y, s + ct) ̺−(x, y, s − ct) 2cdt ds dx dy 2c = relative velocity of bunches in laboratory system, fc = c/b = collison frequency, b distance between successive bunches. Gaussian distributions ̺±, also include [horizontal] crossing angle 2θ ≪ 1: 2 2 2 (x±sθ ) (s±ct) y ± − − − N 2 2 2 2σx (s) 2σy (s) 2σs e . ̺±(x, y, s ± ct) = (2π)3/2σx(s)σy (s)σs Andreas Streun, PSI 160 7. Luminosity Hourglass effect Focus at collision point (∗) : σu(s) = σu∗ Z =⇒ fcN +N − ·S L= ∗ ∗ 4π σxσy r 1+ 2 s ∗ βu , −→ A∗ = 4πσx∗ σy∗ u = x; y for Gaussian beams Luminosity suppression factor hourglass effect 2 S=√ π σs Z∞ 0 2 − σss x e ( ) e r 2 r 2 ds 1 + βs∗ 1 + βs∗ x Limit on focus: β ∗ > σs Andreas Streun, PSI 2 θs − σ (s) y −→ S ≈ 0.8 . . . 0.95 161 7. Luminosity Space charge limit Space charge limit Lens formed by oncoming Gaussian bunch with integrated strength Z 2re N∓ ∆u′ fu(x, y) =− ± ∗ ∗ k ds = u γ σu(σx + σy∗) u = x, y µoc2 re = 4πmo Form factors fu, non-linear and coupling. fu = 1 for x, y ≈ 0 (beam core). Calculate maximum distortion of machine tune 1 ± ∆Qu = 4π Z 1 ∗ k βu(s) ds ≈ βu 4π Z (like in chromaticity derivation): N ∓βu∗ re ± =: ζ k ds = u 2πγ ± σu∗ (σx∗ + σy∗) ζ = space charge parameter or linear tune shift parameter. Empirical limit: ζ < 0.05 in e+e−, ζ < 0.005 in pp̄ collision. =⇒ phase space current saturation: ζ ∼ N ǫxo Assume N + = N − and match beam parameters to reach current limit in x and y Andreas Streun, PSI 162 7. Luminosity −→ Luminosity optimization βy∗ βx∗ = ζy ζx V g= ǫy ǫx =⇒ = ζx ζy V with beam aspect ratio V = σy∗ ∗ σx cπ 2 (1 + V )2 ǫxo ζxζy S L= 2γ re 1 + g b βy∗ Limiting cases: round beam V = g = 1, ideal flat beam V = g = 0. How to optimize luminosity: • large natural emittance ǫxo → ”fill the aperture”: p ! 2 nσx(s) = n ǫxβx(s) + (σδ D(s)) ≤ ax(s) with ax the horizontal aperture and n sigma stay clear. • sharp focus – but . . . ⊲ βy∗ > σs for S ≈ 1. ⊲ longitudinal beam beam effect: energy modulations for large x′∗ , y ′∗ ⊲ tune shift aggravation: ∆Q > ζ for ∆s 6= 0. • short distance b between successive bunches. Limit b = λrf . Avoid parasitic crossings (approx. criterion for encounters: ∆y > 2.5σx.) Andreas Streun, PSI 163 7. Luminosity Tune spread Tune spread Non-linearity of beam-beam lens =⇒ Tune spread (beam’s footprint) Force vs. position: Ref.: W.T.Weng,Space charge effects, tune shifts and resonances, SLAC-PUB-4058, Aug.1986 Andreas Streun, PSI 164 7. Luminosity Beam-beam limit Beam-beam limit Saturation current Coupling of betatron oscillations due to beam beam lens =⇒ vertical blow-up of flat beam, increase of interaction area =⇒ saturation of space charge parameter, only linear luminosity increase from: R.Talman, Specific luminosity limits of e+ e− colliders, PRST AB 5, 081001 (2002) Andreas Streun, PSI 165 7. Luminosity Beam separation Beam separation Magnetic separation for head-on collision of identical particles (e− e− or pp) at same energy Asymmetric magnetic separation for head-on collision of particleantiparticle at different energies to boost the center-of-mass system. Electrostatic separation for head-on collision of particle-antiparticle at same energy. Crossing angle (∼ 10 mrad) for fast separation. Allows high bunch frequency, but luminosity is reduced due to incomplete overlap. Also risk of instabilities. (note: bunch height ≪ width ≪ length) Andreas Streun, PSI Crab-crossing for head-on collision of bunches of crossing beams. A pair of transverse deflecting cavities applies time dependant transverse momentum to the bunches of both beams, causing a tilt (“crab walk”). Focusing lenses invert the momentum, and another pair of cavities compensates the modulation. Particle factories work with crossing beams to achieve high bunch frequency. Some use crab-crossing or crab waist to increase luminosity. 166 7. Luminosity Beam separation Crab crossing Crossing at angle 2θ + high bunch frequency − reduced overlap / luminosity =⇒ restore head-on collision: transverse deflecting cavities at ∆φx = ±90◦ before/after interaction point. (in use at KEK B-factory, reached L > 1034cm−2s−1.) Andreas Streun, PSI 167 7. Luminosity Beam separation Crab waist Crossing at angle 2θ ≪ 1 + reduced interaction length for σx ≪ σs σx =⇒ criterion βy∗ > σs → βy∗ > [sin]2 θ ≪ σs p eff. beam width σ̄x = σx2 + (σs tan θ)2 ≈ σsθ L∝ N2 N2 σy σ̄x −→ σy (σs θ ) ζx ∝ N βx∗ N βx∗ σ̄x (σ̄x +σy ) −→ (σs θ )2 ζy ∝ N βy∗ N βy∗ σy (σ̄x +σy ) −→ σy (σs θ ) 1. θ ↑, N ↑ (N p ∝ θ) → ζy const., ζx ∝ 1/N ↓, L ∝ N ↑ Luminosity increase 2. βy∗ ↓, (σy ∝ βy∗) → ζy ∝ σy ↓, L ∝ σ1y ↑ Problem: coupling resonances → adjust s-position of focus to coincide with oncoming bunch centre by means of sextupoles: crab sextupoles OFF Andreas Streun, PSI crab sextupoles ON 168 7. Luminosity Beam separation ↑ Horizontal variation of focal length ↓ Suppression of vertical blow-up Expected luminosity increase P.Raimondi, M.Zobov, R.Shatilov, Suppression of beam-beam resonances in crab waist collisions, Proc.EPAC 2008, p.2620 Andreas Streun, PSI 169 7. Luminosity Beam disruption Beam disruption Linear colliders: no re-use of beam −→ no limit on ζ-parameters −→ beam-beam lens: focal length < bunch length, f < σs −→ self-focussing (pinch-effect) −→ luminosity enhancement −→ beam disruption, parameter du = σs f = 2re N σs ∗ ∗ +σ ∗ ) γ σu (σx y = −4πζu βσ∗s u u = x; y Linear collider luminosity limitations: • sub-µm alignment of final focus • beamstrahlung = synchrotron radiation in magnetic field of oncoming bunch ⊲ photon recoil → undefined center-of-mass energy ⊲ direct gamma-background ⊲ pair production background Andreas Streun, PSI 170 8. Muon accelerators and neutrino factories ⊲ Physics Muons and neutrinos ⊲ Neutrino factories Beta decay. Pion and muon decay. Muon decay in storage ring. ⊲ Muon accelerator challenges Proton drivers. High power targets. Pion capture in magnetic horn. Muon cooling by ionization. FFAG (fixed field alternating gradient cyclotron) ⊲ Spallation neutron sources Andreas Streun, PSI 171 Muon accelerators and neutrino factories Physics Muons and neutrinos Muon = ”heavy electron”, mµ = 207 me Muon circular collider γ 207 times lower at same center of mass energy, synchrotron radiation loss P ∼ γ 4 only 10−9 of electrons. =⇒ leptonic collisions at large Ecm (TeV) with ”compact” collider. Neutrino factory Physics interest in high energy neutrinos (cross section ∼ energy). → how to create high energy neutrino beams of reasonable luminosity? Neutrino oscillation studies → long baseline experiments (> 1000 km) Andreas Streun, PSI 172 Muon accelerators and neutrino factories Neutrino factories Neutrino production 1. Electron neutrinos from beta decay Decay of radioactive ions stored in ring, e.g. 6 2 He −→ 6 3 Li + e− + ν̄e or 18 10 Ne −→ 18 9F + e+ + νe Project BetaBeam at CERN → Components: ⊲ proton driver ⊲ ion production ⊲ ion accelerators ⊲ storage and decay ring storage ring with long straights to obtain collimated neutrino beam Andreas Streun, PSI 173 Muon accelerators and neutrino factories Neutrino factories 2. Neutrinos from pion and muon decay High energy proton beam on target: p → π +, π −, π o . . . Muon-neutrinos from pion decay: π + → µ+ + νµ and π − → µ− + ν̄µ Muon- and electron neutrinos from muon decay: µ+ → e+ + ν̄µ + νe µ− → e− + νµ + ν̄e Neutrino factory components: ⊲ high intensity proton driver ⊲ high power production target ⊲ muon capture and focussing In operation: ν CNGS CERN =⇒ Gran Sasso T2K ν J-PARC =⇒ Kamioka Andreas Streun, PSI ր 174 Muon accelerators and neutrino factories Neutrino factories 3. Neutrino beams from muon decay in storage ring Additional components of neutrino factory: ⊲ muon ionization cooler or damping ring, ⊲ rapid muon acceleration, ⊲ inclined muon storage ring Neutrino beam apex towards distant detectors. Projects at JAERI, CERN, BNL, FNAL, RAL Andreas Streun, PSI 175 Muon accelerators and neutrino factories Muon accelerators Muon accelerator challenges Proton drivers∗ −→ cyclotrons and linacs Megawatt targets∗ (π/µ production) liquid metal [jet] −→ Muon capture (focus muons after target) −→ magnetic horn Muon cooling (compress 6d-phase space) −→ ionization cooling Muon acceleration (very fast acceleration) −→ • recirculated linacs • VRCS (very rapid cycling synchrotron) • FFAG (fixed field alternating gradient cyclotron) ∗ common interest with spallation neutron sources for materials research and energy production Andreas Streun, PSI 176 Muon accelerators and neutrino factories Proton drivers Proton drivers Beam power > 1 MW ! Cyclotrons PSI: P = 1.3 MW (operating) Linacs CERN SPL (Superconducting Proton Linac) P = 4 MW (>2010) Andreas Streun, PSI 177 Muon accelerators and neutrino factories Targets High power targets Problems: Thermal stress (P > 1 MW in small volume) and nuclear activation ← PSI rotating graphite wheel target for pion production (≈ 100 kW, operating temperature 1700◦C, lifetime ∼ 1 year) PSI MegaPie liquid metal (Pb/Bi) target → for SINQ neutron source (1.0 MW) ↓ BNL prototype for liquid metal jet target Andreas Streun, PSI 178 Muon accelerators and neutrino factories Pion capture Magnetic horn Pion focusing at production target: Andreas Streun, PSI 179 Muon accelerators and neutrino factories Muon cooling Ionization cooling Electrons: radiation cooling decrease of total momentum due to radiation increase of ps only by acceleration −→ damping of transverse momenta but: increase of momentum spread due to stochastic photon emission −→ minimize by focus in bending magnets Muons: ionization cooling = friction decrease of total momentum due to multiple ionization of atoms increase of ps only by acceleration −→ damping of transverse momenta but: increase of momentum spread due to stochastic scattering events −→ minimize by focus in medium Andreas Streun, PSI 180 Muon accelerators and neutrino factories Muon cooling MICE Muon Ionization Cooling Experiment Andreas Streun, PSI 181 Muon accelerators and neutrino factories Muon cooling MICE results Simulations of emittance damping Ref.: M.Appollonio & J.H.Cobb Emittance measurement in MICE J.Physics, Conf.Ser., 110(2008)122002 Andreas Streun, PSI Measured damping of transverse emittance 182 Muon accelerators and neutrino factories Muon cooling Muon cooling rings R.Edgecock, RAL Andreas Streun, PSI 183 8. Muons accelerators and neutrino factories Muon cooling Helical cooling channels continuous focusing and dispersion along helical path Ö exchange transverse ↔ longitudinal Ö 6-D phase space cooling Emittances as function of length ↓ Andreas Streun, PSI Figures taken from Yonehara et al., PAC’05, p.3212 and Bross et al., Proc.COOL-2009 184 8. Muons accelerators and neutrino factories Muon acceleration FFAG (Fixed Field Alternating Gradient cyclotron) Machine Field Radius Frequency Tunes Q(E) Synchrotron & betatron variable fixed fixed constant Microtron & cyclotron fixed variable fixed ~constant FFAG (scaling) fixed variable variable constant FFAG (non scaling) fixed variable fixed variable FFAG: + fast acceleration + large momentum aperture Ö muons! Scaling FFAG: fast acceleration avoid resonance crossing Ö tunes, betas etc. constant on ramp Ö wide orbit range Ö complicated magnet design Andreas Streun, PSI Non-scaling FFAG even faster acceleration: few turns only Ö ignore resonances Ö keep RF constant Ö asynchronous acceleration (no bucket!) Ö stability ? Ref. M. Craddock, Proc. PAC’05, p.261 185 8. Muons accelerators and neutrino factories Muon acceleration PRISM FFAG for muon phase rotation phase rotation = 90º rotation in (∆E,∆s) space to reduce energy spread on expense of bunch length Challenging magnet design: wide aperture and achromatic, i.e. Q ≠ Q(E) magnet field profiles → Ref.: A. Sato, A Fixed Field Alternating Gradient Ring for a High Intensity Monochromatic Muon Source Andreas Streun, PSI phase space motion 186 8. Muons accelerators and neutrino factories Muon acceleration Scaling FFAGs 150 MeV proton FFAG at KEK ↓ ↑ LAPTOP 1 MeV electron FFAG for industrial and medical applications (∅ ∅ 10 cm ! ) Andreas Streun, PSI 187 8. Muons accelerators and neutrino factories Muon acceleration Non-scaling FFAG Prototype EMMA Electron Model for Muon Accelerator (10...20 MeV) Daresbury Laboratory (UK) Ref.: R. Edgecock et al., Proc. EPAC’08, p.3380 Future plans: proton FFAG 10→20 GeV in 16 turns Andreas Streun, PSI 188 8. Muons accelerators and neutrino factories Neutron sources Spallation neutron sources Spallation: high energy proton excites nucleus → emission of several neutrons and protons. Normalized yield neutrons/proton as function of incident proton energy → Ref.: A. Letourneau et al., Neutron production in bombardments of thin and thick W, Hg, Pb targets by 0.4, 0.8, 1.2, 1.8 and 2.5 GeV protons, Nucl. Instr. and Meth. in Phys. Res. B 170 (2000) 299-322 Ö requires GeV-proton beam of MW power SINQ Spallation neutron source at PSI for materials research (includes MEGAPIE liquid metal target) Andreas Streun, PSI 189 SNS and ESS Spallation Neutron Source Oakridge, USA Power: 1.0 (1.4) MW 1 GeV protons n.c linac → 200 MeV s.c. linac → 1 GeV liquid Hg target start of operation 2006 budget 1.4 G$ Andreas Streun, PSI SNS liquid Hg target ¯ESS artist’s view European Spallation Source Lund, Sweden 18 partner countries Power 5.0 MW 1 GeV protons n.c linac → 400 MeV s.c. linac → 1 GeV liquid Hg or Pb target start of project 1993 decision on site 2009 start of operation 2019 fully operational 2025 budget 1.5 G€ 190 8. Muons accelerators and neutrino factories Neutron sources ADS: accelerator driven “system” = accelerator driven nuclear fission reactor = spallation neutron source Synergy with muon accelerators multi-MW proton accelerator multi-MW liquid metal target ADS advantages (promises) sub-critical: inherent safety nuclear waste incineration little transuranic production (239Pu!) reduced risk of proliferation fuel breeding: 232Th → 233U more tolerant to bad maintenance Andreas Streun, PSI 191 Summary Particle Physics... Synchrotrons and linacs... Dipole magnets are used for bending, Quadrupoles are usually used for focusing, Sextupoles compensate chromatic focusing errors. Beam transformation... are the most important accelerators for particle physics, are based on radio frequency (RF) acceleration, and thus have “bunched” particle beams. Magnets (iron or superconducting) shape the beam: depends on accelerators, drives the development of new accelerators, shares common accelerator needs with material research. is described by concatenation of element matrices in the linear case, decouples guide field (beta-function) and phase space (emittance). Beam phase space density... determines the performance of the experiments (luminosity) is constant in many cases (Liouville theorem), can be enhanced through cooling processes (synchrotron radiation, ionization). Andreas Streun, PSI 192