* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download torque and circular motion - PHYSICS I PRE-AP
Roche limit wikipedia , lookup
Artificial gravity wikipedia , lookup
Torque wrench wikipedia , lookup
Friction-plate electromagnetic couplings wikipedia , lookup
Centrifugal force wikipedia , lookup
Coriolis force wikipedia , lookup
Fictitious force wikipedia , lookup
Weightlessness wikipedia , lookup
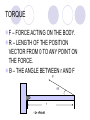
TORQUE AND CIRCULAR MOTION CHAPTER 8 TORQUE A PHYSICAL QUANTITY RESPONSIBLE TO CREATE ANGULAR ACCELERATION FO A BODY. IT STARTS, STOPS, OR CHANGES THE DIRECTION OF THE MOTION. IT IS PRODUCED BY A FORCE APPLIED ON A BODY. Ł= rFsinθ TANGENTIAL AND RADIAL COMPONENTS A FORCE HAS A TANGENTIAL AND A RADIAL COMPONENT THE RADIAL COMPONENT GOES THROUGH THE AXIS OF ROTATION AND SO DOES NOT CAUSE ROTATION THE TANGENTIAL COMPONENT IS THE ONE THAT CAUSES ROTATION DIAGRAM OF TORQUE PHI IS THE ANGLE F MAKES THE ANGLE OF ROTATION τ=rFsin Φ F Φ MOMENT ARM – PERPENDICULAR DISTANCE OF THE LINE OF ACTION OF THE FORCE FROM THE AXIS TO ROTATION. (MOMENT ARM IS ALSO CALLED LEVER ARM) FR FT P O MOMENT ARM τ=Fperpendicular OR FIND THE COMPONENT OF THE FORCE CAUSING THE TORQUE TORQUE F – FORCE ACTING ON THE BODY. R – LENGTH OF THE POSITION VECTOR FROM 0 TO ANY POINT ON THE FORCE. Θ – THE ANGLE BETWEEN r AND F F θ r Ł= rFsinθ RESOLVE THE FORCE INTO X & Y WHEN TORQUE IS APPLIED, ROTATION OCCURS AROUND PIVOT POINT OR FULCRUM F F sin θ θ F cos θ PIVOT POINT(FULCRUM) DIRECTION OF ROTATION ROTATION IS TAKEN IN A SINGLE PLANE ROTATION CAN BE CLOCKWISE ROTATION CAN BE COUNTERCLOCKWISE SIGN CONVENTION FOR TORQUE TORQUE – CLOCKWISE IS NEGATIVE COUNTERCLOCKWISE IS POSITIVE NET TORQUE THE SUM OF ALL TORQUES ACTING ON THE BODY. THE SUM IS CARRIED OUT TAKING INTO ACCOUNT THE SIGN CONVENTION. WHEN MORE THAN ONE TORQUE ACTS ON A BODY, THE ACCELERATION PRODUCED IS PROPORTIONAL TO THE NET TORQUE. CENTER OF GRAVITY THE POINT AT WHICH THE ENTIRE WEIGHT OF AN OBJECT SEEMS TO ACT. SEE-SAW TORQUE UNIFORM IF AN OBJECT IS UNIFORM ITS CENTER OF GRAVITY IS AT ITS GEOMETRIC CENTER. CENTER OF MASS THE POINT WHERE ALL THE MASS SEEMS TO ACT. AN OBJECT IS IN EQUILIBRIUM AS LONG AS THE CM STAYS OVER ITS BASE LEVEL AN OBJECT IS CONSIDERED UNIFORM WHEN THE CM IS ITS GEOMETRIC CENTER XCM=1/M Σ mi xi M = TOTAL MASS Mi = MASS OF PARTCLE Xi = DISTANCE FROM THE ORIGIN MECHANICAL EQUILIBRIUM ANY MOTION OF A RIGID BODY IS A CONBINATION OF ROTATIONAL AND TRANSLATIONAL MOTION IT IS SAID TO BE IN MECHANICAL EQUILIBRIUM IF THE TRANSLATION AND ROTATIONAL MOTION ARE IN EQUILIBRIUM CONDITIONS ROTATIONAL EQUILIBRIUM Σ τ(ABOUT ANY POINT) = 0 (ANGULAR MOMENTUM IS CONSTANT) TRANLATIONAL EQUILIBRIUM ΣFx = 0 AND ΣFy = O AND ΣFz = O ELASTICITY THE BRANCH OF PHYSICS WHICH DEALS WITH HOW OBJECTS DEORM WHEN FORCES ARE APPLIED TO THEM. ELASTIC LIMIT- WHEN PERMANENT DEFORMATION OCCURS AND THE OBJECT WILL NOT RETURN TO ITS ORIGINAL SHAPE. THREE WAYS AN OBJECT CHANGES ITS SHAPE SHEARING FORCES – CAUSE MOVEMENT SIMILAR TO THE PAGES OF A BOOK. EX: EARTH LAYERS DURING A QUAKE. STRETCHING OR COMPRESSING FORCES. EX: BALLOON, STRING BULK FORCES – APPLIES TO FLUIDS. PRESSURE FROM ALL SIDES CAN CAUSE A VOLUME CHANGE. STRESS AND STRAIN STRESS(CAUSED BY FORCES) PRODUCE STRAIN. STRESS IS PROPORTIONAL TO STRAIN THAT PROPORTIONALITY CONSTANT IS CALLED THE MODULUS(E) (YOUNG’S MODULUS) EQUATIONS STRETCHING STRESS = FORCE/AREA OVER WHICH THE FORCE IS APPLIED STRAIN = ratio of the change. The ratio could be length, volume, height STRAIN = ∆L/L OR ∆H/H OR ∆V/V STRESS = E x STRAIN EQUATIONS STRETCHING FORCES F/A=E∆L/L SHEARING FORCES F/A=G∆H/H G = SHEARING MODULUS BULK FORCES F/A=B∆V/V B = BULK MODULUS REMEMBER: PRESSURE = F/A UNIT FOR THE MODULUS IS PASCALS ROTATIONAL MOTION PURE ROTATIONAL MOTION IS MOTION WHERE ALL POINTS OF THE OBJECT MOVE IN A CIRCULAR PATH AROUND AN AXIS OF ROTATION. WE ARE MOST CONCERNED WITH RIGID BODIES – BODIES THAT DO NOT DEFORM WITH MOTION. TWO TYPES OF VELOCITY –RIGID OBJECTS LINEAR VELOCITY – GREATER THE FURTHER FROM THE AXIS OF ROTATION. M/S ANGULAR VELOCITY IS THE SAME FOR EVERY POINT IN THE ROTATING BODY AT ANY GIVEN INSTANT. RAD/S OR REV/S PICTURE THIS AN OBJECT ROTATES FROM POINT A TO B IN THE SAME ANGLE AS FROM POINT a TO b. A BOTH TRAVEL THE SAME ANGULAR DISTANCE – θ a θ B b TANGNTIAL DISTANCE THEY TRAVELED DIFFERENT TANGENTIAL DISTANCES IN THE SAME TIME PERIOD. ARC LENGTH AB > ARC LENGTH ab A a θ B b ANGULAR DISPLACEMENT THE ANGLE THROUGH WHICH AN OBJECT TURNS AROUND AN AXIS OF ROTATION. MEASURED IN DEGREES, RADIANS, OR REVOLUTIONS 1 REV = 360° = 2π RADIANS Θ = D/R D – TANGENTIAL DISTANCE R - RADIUS CONVERSION BETWEEN METERS AND RADIANS (TRANSLATIONAL TO ROTATIONAL) DISTANCE IN METERS = RADIANS RADIUS IN METERS A RADIAN IS A UNIT THAT SERVES AS A PLACE HOLDER ANGULAR POSITION GIVEN AS THE OBJECT HAS ROTAED THROUGH SOME ANGLE WHEN IT TRAVELS THE DISTANCE “L” MEASURED ALONG THE CIRCUMFERENCE OF ITS CIRCULAR PATH. WHAT IS A RADIAN ONE RADIAN (RAD) IS THE ANGLE SUBTENDED BY AN ARC WHOSE LENGTH IS EQUAL TO THE RADIUS. IN OTHER WORDS, IF L=R, THEN θ IS EXACTLY EQUAL TO ONE RADIAN ANGULAR SPEED – VELOCITY ώ THE RATE AT WHICH AN OBJECT ROTATES RADIANS/SECOND ω = θ/t ω = V/R (V IS TANGENTIAL V) ω = ∆θ/t ANGULAR SPEED AND FREQUENCY FREQUENCY IS THE NUMBER OF COPELTE REVOLUTIONS PER SECOND 1 REV/S = 2πRADIANS/S f = ω / 2π ANGULAR ACCELERATION (α) THE RATE AT WHICH A ROTATING OBJECT CHANGES ANGULAR SPEED RADIANS/S2 α = (ωf - ωi)/T α = A/R A IS TANGENTIAL ACCELERATION R = RADIUS AVERAGE ANGULAR ACCELERATION α = ∆ω/t TOTAL LINEAR ACCELERATION THE VECTOR SUM OF THE CENTRIPETAL ACCELERATION (THE RADIAL COMPONENT OF THE ACCELERATION) aR = ω2r AND THE TANGENTIAL COMPONENT OF THE ACCLERATION. DIAGRAM BECAUSE OF THIS THE CENTRIPETAL ACCELERATION INCREASES THE FARTHER YOU ARE FROM THE AXIS OF ROTATION. a tan aR EQUATION COMPARISON EQUATIONS FOR LINEARMOTION CAN BE TRANFORMED INTO ROTATIONAL FORMS D=V/T D=Do+Vi + ½ at2 Vf=Vi + at Vf2 = Vi2 + 2ad θ = ωt θ = θo + ωi t + ½ αt2 ωf = ωi+ αT ωf 2= ωi2+ 2αθ NEWTON’S 2ND LAW IN ROTATIONAL FORM F = MA …… Ł = Iα Ł - TORQUE I – MOMENT OF INERTIA α – ANGULAR ACCELERATION ROLLING WHEEL TANGENTIAL VELOCITY OF THE WHEEL AT THE AXEL = V TANGENTIAL VELOCITY OF THE WHEEL AT THE EDGE = 2V MOMENT OF INERTIA, I ANALAGOUS TO MASS DEPENDS UPON THE ROTATING BODY’S MASS AND THE DISTRIBUTION OF THE MASS I = ΣM1R12 + M2R22 + M3R32 …. HOW UNITS COMPARE VARIABLE TRANSLATIONAL ROTATIONAL DISTANCE d – METERS Θ - RADIANS VELOCITY V – M/S ω – RADIANS/S ACCLERATION a – M/S2 Α – RADIANS/S2 FORCE F – NEWTONS Ł–Nm MASS m – KILOGRAMS I – kg m2 MOMENT OF INERTIA A FORCE IS REQUIRED TO START AN OBJECT ROTATING ABOUT AN AXIS. TORQUE PRODUCES ANGULAR ACCELERATION. TORQUE IS REQUIRED TO START THE ROTATION THE MOMENT OF INERTIA TELL HOW THE MASS OF THE BODY IS DISTRIBUTED ABOUT THE AXIS. Ł = Iα ROTATIONAL MOMENT OF INERTIA FOR BODIES THIN HOOP OF RADIUS R I = mr2 SOLID DISK OF RADIUS R I = 1/2 mr2 UNIFORM SPHERE OF RADIUS R I = 2/5 mr2 LONG UNIFORM ROD OF LENGTH L WITH ITS I = 1/12 mr2 AXIS OF ROTATION THROUGH ITS CENTER LONG UNIFORM ROD OF LENGTH L WITH ITS I = 1/3 mr2 AXIS OF ROTATION THROUGH ONE END ROTATIONAL K.E. ROTATION AROUND THE CM MEASURED IN JOULES KE = ½ Iω2 ROTATION OF OBJECT NOT AROUND THE CENTER OF MASS HAS ROTATIONAL AND TRANSLATIONAL K.E. KE = ½ mv2 + ½ Iω2 SLIDING VS ROLLING OBJECTS THAT SLIDE CONVERT ALL OF THEIR POTENTIAL ENERGY INTO TRANSLATIONAL KINETIC ENERGY. OBJECTS THAT ROLL CONVERT MOST OF THEIR POTENTIAL ENERGY INTO ROTATIONAL K.E. AND THE REST INTO TRANSLATIONAL K.E. SO IT WILL NOT MOVE AS QUICKLY AS A SLIDING OBJECT. ANGULAR MOMENTUM p=mv – LINEAR L = Iω – ANGULAR ANGULAR MOMENTUM REMAINS CONSTANT IF NO EXTERNAL TORQUES ARE ACTING IF TORQUE NET IS ZERO AND ROTATION IS AROUND A FIXED AXIS THE MOMENTUM IS CONSERVED Iω = CONSTANT EXAMPLE ICE SKATER SPINNING ON ICE – EXTENDED ARMS INCREASE I AND GIVE A SMALL ω AS SHE BRINGS HER ARMS IN THE I DECREASES SO THE ω INCREASES BECAUSE ANGULAR MOMENTUM IS CONSERVED.