Download Systematic Circuit Analysis

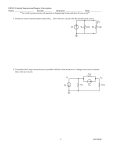
Systematic Circuit Analysis
Nodal Analysis
Chapter 4 Section 1
3 Fundamental Principles
•
Ohm’s Law
 V = I · R, where I enters at the higher
voltage side
•
Kirchoff’s Voltage Law
 Algebraic sum of voltages around a loop
equal zero
•
Kirchoff’s Current Law
 Algebraic sum of currents entering and
leaving a node equal zero
Circuit Simplification
• Series Resistors can be combined into a
single equivalent resistance
• Parallel Resistors can be combined into a
single equivalent resistance
• Current sources in parallel add
algebraically
• Voltage sources in series add algebraically
• A voltage source is series with a resistor
can be replaced by a current source in
parallel or vice versa
Shortcuts
• Voltage Divider – a voltage dividing across
a series combination of resistors
– Largest voltage is across the largest resistor
• Current Divider – a current dividing among
a parallel combination of resistors
– Largest current is through the smallest
resistor
Nodal Analysis
• Employs the 3 fundamental laws
• May not require any circuit simplification
• Consists of a straight-forward step-by-step
procedure
• Involves the solution of a set of linear
equations simultaneously
• Used by most circuit analysis computer
programs like PSpice
Example
• Find the voltages and currents
Step One
• Identify all nodes that have at least 3
components connected to them
• Choose one of the above nodes as the
ground, or reference node, Vo=0 volts
• Label the other nodes with V1, V2, etc.
Voltage Notation
• Remember that voltage is always
measured with respect to some other point
• So V1 the voltage at node 1 minus the
voltage at node 0, or V1-Vo = V10 = V1
• V12 would be the voltage at node 1 minus
the voltage at node 2, or V12 = V1-V2
Voltage Notation
• V12 could also be obtained by going
through any path, say node 3
V12 = V132 where V132 = V13 + V32
But V13 + V32 = (V1-V3) + (V3-V2)
And (V1-V3) + (V3-V2) = V1-V2 = V12
Circuit After Step One
V1
Vo = 0 volts
Step Two
• Choose currents for every circuit branch
that is connected to any of the unknown
voltage nodes
– In this circuit, choose currents for the
branches connected to V1
– You can also label voltages at other nodes in
the circuit (nodes that have only two
components), Va and Vb
Circuit after Step Two
I1
Va
+
V1
-
I3
+
+
I2
-
Vo = 0 volts
-
Vb
Step Three
• Find the value of each current or find an
expression for each current in terms of the
unknown voltages, V1, V2, etc.
• The idea is to get all the currents to be
expressed in terms of the node voltages,
so that a KCL equation can be written at
each unknown node, giving us as many
equations as unknowns
Step Three
• If you have a resistor between two nodes,
then the current is the voltage at the node
where the current originates minus the
voltage at the other node divided by the
resistance (Ohm’s Law)
• For this circuit the 10Ω resistor is between
nodes 1 and ground (node 0)
I2 = (V1 – 0) / 10Ω = V1 / 10Ω
Step Three Cont.
• If you have a resistor and a series voltage
source between two key nodes, determine
the voltage at the node between the
components and then use Ohm’s law
• There is a 6v source and 14Ω resistor in
series between node 1 and ground
Va = Vo+6v. = 6v.
I1 = (Va - V1) / 14Ω = (6v - V1) / 14Ω
Step Three Cont.
• There is also 5v source and 10Ω resistor
in series between node 1 and ground
• Determine the voltage at the intermediate
node
 Vb = Vo+5v. = 5v.
• Use Ohm’s law to determine the current
I3 = (V1-Vb) / 14Ω = (V1-5v) / 10Ω
Circuit after Step Three
Va=6v
I1=(6-V1)/14Ω
V1
+
-
I3=(V1-5)/10Ω
+
-
+
I2 =
V1/10Ω
-
Vo = 0 volts
Vb=5v
Step 4
• Write Kirchoff’s Current Law at each node
with an unknown voltage
I1 = I2 + I3
• Substitute each value or expression into
each KCL equation
(6v-V1)/14Ω = V1/10Ω + (V1-5v)/10Ω
Step 5 Solve
• Solve the set of equations for each
unknown voltage
(6v-V1)/14Ω = V1/10Ω + (V1-5v)/10Ω
• Multiply both sides to clear fractions
70Ω·[(6v-V1)/14Ω = V1/10Ω + (V1-5v)/10Ω]
30v - 5·V1= 7·V1 + 7·V1 - 35v
• Group like terms and solve
65v = 19·V1 or V1 = 3.42v
Step 5 Solve Cont.
• Since V1 = 3.42v
• Find each current by substituting the
voltage values found into each current
equation as appropriate
I1 = (6v-V1)/14Ω = (6-3.42)/14 = .184 A
I2 = V1/10Ω = 3.42/10 = .342 A
I3 = (V1-5v)/10Ω = (3.42-5)/10 = -.158 A
Step 6 – Reality Check
Va=6v
I1=.184A
+
-
I3= -.158A
V1=3.42v +
+
I2=
.342A
-
Vo = 0 volts
Vb=5v
Example with a Dependent Source
• Find the voltages and currents
I1
Handling the Dependent Source
• The dependent source will be dependent
on some voltage or current in the circuit
• You will need to express that voltage or
current in terms of the unknown node
voltages
• The idea is to only use the node voltages
in finding the currents so that there will be
as many KCL equations as variables
Step One
• Identify all nodes that have at least 3
components connected to them
• Choose one of the above nodes as the
ground, or reference node at zero volts
• Label the other nodes with V1, V2, etc.
Circuit after Step 1
I1
V1
Vo = 0 volts
Step Two
• Choose currents for every circuit branch
that are connected to any of the unknown
key voltage nodes
Circuit after Step 2
I1
V1
+
-
+
I2
-
- I3
+
Vo = 0 volts
Vb
Step Three
• Find the value of each current or find an
expression for each current in terms of the
unknown voltages, V1, V2, etc.
If you have a resistor between two nodes,
then the current is the voltage at the node
where the current originates minus the
voltage at the other node divided by the
resistance (Ohm’s Law)
I2 = (V1 – 0) / 4Ω = V1 / 4Ω
Step Three Cont.
• If you have a resistor and a series voltage
source between two nodes, determine the
voltage at the node between the
components and then use Ohm’s law
Vb = Vo+3v. = 3v.
I1 = (V1-Vb) / 2Ω = (V1-3v) / 2Ω
Step Three Cont.
• If you have multiple resistors and/or
voltage sources between two key nodes,
combine them together to get one resistor
and one source
If there is a dependent part of the source,
express it in terms of the unknown node
voltages
Determine the voltage at the node between
the equivalent resistor and source
 Use Ohm’s law
Circuit for Step 3
I1
V1
Va
+
-
5v + 4Ω·I1
+
I2
-
- I3
+
Vo = 0 volts
Vb=3v
Vb
Step Three Cont.
• The combined dependent source is
5v+4Ω·I1
So Va = V1 – (5v+4Ω·I1)
But I1 in the dependent source was
determined to be (V1-3v)/2Ω
So Va = V1–(5v + 4Ω·(V1-3v)/2Ω) = -V1+1
• I3 = (Vo-Va) / 4Ω = (0-(-V1+1)) / 4Ω
I3 = (V1 -1v) / 4Ω
Circuit for Step 4
Va=
1v-V1
V1
I1=(V1-3)/2Ω
+
-
5v + 4Ω·I1
+
I 2=
V1/2Ω
+
I3=(V1-1)/4Ω
Vo = 0 volts
Vb=3v
Vb
Step 4
• Write Kirchoff’s Current Law at each node
with an unknown voltage
I3 = I2 + I1
• Substitute each value or expression into
each KCL equation
(V1 -1v) / 4Ω = V1 / 4Ω + (V1-3v) / 2Ω
Step 5 Solve
• Solve the set of equations for each
unknown voltage
(V1 -1v) / 4Ω = V1 / 4Ω + (V1-3v) / 2Ω
• Multiply both sides to clear fractions
4Ω·[(V1 -1v) / 4Ω = V1 / 4Ω + (V1-3v) / 2Ω]
V1 - 1v = V1 + 2·(V1-3v)
• Group like terms and solve
5v = 2·V1 or V1 = 2.5v
Step 5 Solving for Currents
• Finding each current:
• I3 = (V1 -1v) / 4Ω = (2.5v -1v) / 4Ω = .375 A
• I2 = V1 / 4Ω = 2.5v / 4Ω = .625 A
• I1 = (V1-3v) / 2Ω = (2.5v-3v) / 2Ω = -.25 A
Step 6 - Checking
I1= -.25A
V1=2.5v +
Va=
1v-V1=
-1.5v
5v+4Ω·I1=4v
+
I2=
.625A
+
I3=.375A
Vo = 0 volts
Vb=3v
Vb
Class Activity
• Find the current equations at node 1
Class Activity
• Find I2 in terms of V1
+
_
For a resistor between nodes, use Ohm’s law
Add polarities if not shown (+ at V1, - at V0)
I2 = V1/60Ω
Class Activity
• Find I3 in terms of its value
For a current source between nodes, the
current is fixed by the source
I3 = 2 A
Class Activity
• Find I4 in terms of V1
+
_
+
_
If you have series resistors, combine them
and then use Ohm’s law
I4 = V1/(30+70)Ω = V1/(100Ω)
Class Activity
• Find I1 in terms of V1
Combine series resistors, even if not next to
each other, then find the voltage between the
source and equivalent resistance
Finding I1
+
-
V1
Vo=0v
Va=100v
+
-
V1
100+80=180Ω
Vo=0v
So I1 = (Va-V1)/180Ω = (100-V1)/180Ω
Class Activity
• Find I5 in terms of V1
+
-
The voltage on the right side of the 50Ω
resistor is known, because of the 150v source
I5 = (V1-150v) / 50Ω
Class Activity
• Write KCL equation at node 1
I1 + I3 = I2 + I4 + I5
Substitute all the current equations:
(100-V1)/180+2A=V1/60+V1/100+(V1-150v)/50
Class Activity
(100-V1)/180+2A=V1/60+V1/100+(V1-150v)/50
Multiply both sides by 9000Ω:
5000-50V1+18000=150V1+90V1+180V1-27000
Group: 50000 = 470V1 Solve: V1= 106.4 v
Class Activity
Checking
I1=-.036A, I2=1.773A, I3=2A, I4=1.064A, I5=-.872A
I1+I3= -.036+2 =1.964 A
I2+I4+I5 = 1.773+1.064-.872 = 1.965 A – Yes!
Example with 3 Unknown Nodes
• Find Voltages and Currents
Steps 1 & 2
• Find key nodes, assign one to ground, choose
currents in branches
I1
+
V1
-
I2
+
Va
-
+
+
I4
V3
I3
V2
-
I5
+
-
-
Vo=0 volts
Step 3 – Current Equations
• Currents for resistors between nodes
I1=(V1-V3)/4Ω
I3=(V2-V3)/7Ω
I4=V2/1Ω
I5= V3/5Ω
• Resistor and source between nodes
Va = V1+ 9v
I2 = (Va-V2)/3Ω = (V1+9v-V2)/3Ω
Step 4 – KCL Equations
• KCL Equation at each key node:
At node 1: 0 = I1 + I2 + 8A
At node 2: I2 = I3 + I4
At node 3: 25A + I1 + I3 = I5
• Substituting for each current
At 1: 0 =(V1-V3)/4Ω +(V1+9v-V2)/3Ω +8A
At 2: (V1+9v-V2)/3Ω =(V2-V3)/7Ω + V2/1Ω
At 3: 25A+(V1-V3)/4Ω +(V2-V3)/7Ω = V3/5Ω
At node 1
• 0 =(V1-V3)/4Ω +(V1+9v-V2)/3Ω +8A
• Multiply both sides by 12Ω to clear
fractions
12Ω·[0 =(V1-V3)/4Ω +(V1+9v-V2)/3Ω +8A]
Or: 0 =3·V1-3·V3 +4·V1+36v-4·V2 +96v
• Combining terms
7·V1 -4·V2 -3·V3 = -132v
At node 2
• (V1+9v-V2)/3Ω =(V2-V3)/7Ω + V2/1Ω
• Multiply both sides by 21Ω to clear
fractions
21Ω·[(V1+9v-V2)/3Ω =(V2-V3)/7Ω + V2/1Ω ]
Or: 7·V1+63v - 7·V2 = 3·V2 - 3·V3 +21·V2
• Combining terms
7·V1 -31·V2 +3·V3 = -63v
At node 3
• 25A+(V1-V3)/4Ω +(V2-V3)/7Ω = V3/5Ω
• Multiply both sides by 140Ω to clear
fractions
140Ω·[25A+(V1-V3)/4Ω +(V2-V3)/7Ω =V3/5Ω]
Or: 3500v+35·V1-35·V3+20·V2-20·V3=28·V3
• Combining terms
35·V1 +20·V2 -83·V3 = -3500v
Set of 3 Simultaneous Eqs.
•
•
•
•
7·V1 -4·V2 -3·V3 = -132v
7·V1 -31·V2 +3·V3 = -63v
35·V1 +20·V2 -83·V3 = -3500v
Solve by hand, calculator, or computer
V1 = 5.414 v
V2 = 7.737 v
V3 = 46.316 v