Download The Singlet-Triplet Spectroscopy of 1,3

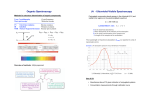
EPAPS Material for File A1.11.205
“The singlet-triplet spectroscopy of 1,3-butadiene
using cavity ring-down spectroscopy”
(Robinson et al.)
Butadiene in the ground state is calculated to be a near-prolate top, and so it was
treated as a prolate symmetric top. The rotational levels of the symmetric top (in the
absence of unpaired electrons) can be described by two quantum numbers, N and K,
where N is the quantum number associated with N, the total angular momentum of the
molecule apart from electron spin, and K is the quantum number associated with the
projection of N onto the symmetric-top axis of the molecule; for a given N, K takes on
values from K = -N, -N+1, ..., N-1, N. In the ground state, the total angular momentum
of the molecule J = N, as there is no spin component, and its quantum number J = N.
Under such circumstances, the energy levels of the prolate symmetric top depend only on
N and K.
E(N,K) = BN(N+1) + (A-B)K2 + DJN2(N+1)2 - DJKN(N+1)K2 + DKK4
(1)
The centrifugal distortion constants DJ, DJK and DK account for the non-rigidity of the
molecule and are usually small compared to A and B; they are assumed to be zero in the
simulation.
Like the ground state, butadiene in the triplet state is expected to be a near-prolate
top and was treated as a prolate top in these calculations. The theory describing the
rotational structure in singlet-triplet vibronic transitions was largely laid out by Van
Vleck in 1951,1 but it wasn’t until Raynes2 that the matrix elements for the non-rigid,
asymmetric rotor in multiplet states were presented. Raynes set forth the matrix elements
for the general case of molecules possessing an orthorhombic or higher symmetry, and
specifically derived expressions for the multiplet splitting in triplet states of symmetric
top molecules. In an electronic state with non-zero spin S, the total angular momentum
of the molecule is now found by J = N + S. Coupling between S and N is what gives rise
to the splitting seen in triplet states. In the limit of small coupling (Hund’s case (b)), N,
S, J and K are all good quantum numbers. Each rotational level in the triplet state splits
into three levels, characterized by J = (N+1), J = N, and J = (N-1) and denoted by F1, F2
and F3, respectively; for N = 0, only J = 0 and 1 are allowed. Raynes determined that in a
molecule of orthorhombic symmetry, only five parameters (a0, a, b,  and ) are needed
to describe the splitting. Furthermore, he determined that for a symmetric top, two of
these parameters (b and ) are zero by symmetry.2 These account for the effect of the
asymmetry on the spin interactions. The constants a0, a, and b are spin-rotation constants
which are functions of the moments of inertia and the distances between the nuclei and
the unpaired electrons. The remaining constants,  and  are functions of the vector
components of the distances between unpaired electrons and are considered spin-spin
constants.
We used the expressions for the multiplet splittings in the triplet state of a
symmetric top given by Herzberg3 which are based on those of Raynes.

(N  1)2  K 2
K2


(N,
K)

(N,K)




(N

1)

2

F1
F0
 (N  1) 2

(N  1)(2N  3)
F 2 (N, K)  F 0 (N, K)  
K2
K2
 2
N(N  1)
N(N  1)
(2a)
(2b)
2
2
 K2

N K
F 3 ( N , K )  F 0 ( N , K )   2    N  2
N (2 N  1)
 N

(2c)
F0(N,K) is the energy of a prolate symmetric top as given above for the singlet state (Eqn.
1). The constants (, , and ) are related to Raynes’ constants (a0, a and ) in the
following way:  = a - a0,  = -3a, and 2 = 3. Typical values for these constants are
small; for glyoxal, Spangler et al.4 report a0 = 0.040, a = 0.006, b = -0.004,  = -0.080,
and  = 0. On the other hand, Judge and Moule report a0 = 0.140, a = 0.14, b = -0.0022,
 = -1.360, and  = 0.09 for thioformaldehyde.5
Hougen described the selection rules governing rotational transitions in singlettriplet spectra in the case of D2h symmetry, the most general point group for asymmetric
top molecules.6 The mixing of singlet state character into the triplet state (arising from
the spin-orbit interaction) will obey the rules J = 0 and P = 0 (where P is the projection
of J along the top axis). In other words, only singlet and triplet states with the same (J,P)
will mix due to the spin-orbit interaction. This restriction, coupled with the usual N =
0,±1 and K = 0,±1 selection rules for a symmetric top, leads to general selection rules
for singlet-triplet transitions of N = 0,±1,±2 and K = 0,±1,±2. The usual selection rule
of J=0,±1 also holds, so the transitions can be divided into P, Q, and R branches, with
each branch containing several sub-bands associated with different N and K values.
The allowed transitions (J, K, N) are divided by Hougen based on the symmetry of
TS, which for molecules of D2h symmetry can be one of four types (Au, B1u, B2u and
B3u). He presented expressions for the intensities of the rotational lines for each of these
four cases. The triplet state of butadiene is 3Bu, while the singlet state is 1Ag, so TS =
Bu, which correlates to B1u and B3u in D2h symmetry.
The intensities of the transitions depend on the quantum numbers of the ground
state and the projections of the transition moment (x, y, and z) onto the three principal
axes. The transition moment projections for the T1  S0 transition of butadiene have
been calculated, and the largest component is in-plane, along the z-axis (roughly parallel
to the double bonds in the molecule).7 Accordingly, we have modeled the transition as a
B1u type transition (Table II from Hougen6), which restricts K to 0, ±2. There will also
be a contribution from a B3u type transition, but that contribution is calculated to be
several orders of magnitude less intense than the B1u component.
Rotational constants for the ground and excited states were calculated using the
optimized geometries from Brink et al.8 Rotational constants for the ground state were
calculated to be A = 1.41 cm-1, B = 0.147 cm-1, C = 0.133 cm-1. Rotational constants for
the triplet state were A = 1.436 cm-1, B = 0.139 cm-1, C = 0.127 cm-1. We used Bave =
(B+C)/2 in the expressions for the energy levels given above. Based on the oscillator
strengths calculated by Mineav et al.,7 the transition moment components were fixed at
z = 1.00 and x = y = 0.020. This left us with three parameters, (, , and ), which
were varied to reproduce the experimental splittings. The calculated spectra were
convoluted with a gaussian (FWHM = 0.25 cm-1) and compared with the experimental
spectrum. The most intense features were due to the Q,RR and Q,RQ (K,NJ) sub-bands,
which are degenerate in the absence of splitting. The Q,PQ and Q,PP branches also carry
some intensity and are also degenerate in the absence of splitting. As the spin-rotation
and spin-spin parameters were changed, a small splitting could be observed in the
calculated spectrum. The splitting arises from a separation of the Q,RR and Q,RQ subbands into two distinct features and it varies linearly with increasing  Varying the other
two parameters over a reasonable range did not produce significant splittings, but at large
values of  ( = 0.5 to 1.5 cm-1), a feature appeared to the blue of the origin which
broadened and moved out farther to the blue as  increased. A value of  in this range is
significantly larger than typical9 and was deemed unrealistic. Varying  shifted the
position of the two main sub-bands slightly relative to the origin but did not produce any
appreciable splitting in the convoluted spectrum. The spectrum shown in Figure 6(a)
was calculated with  = 2.0 and  =  = 0.00. At no point during the survey were more
than two major features observed in the calculated spectrum; accordingly, we conclude
that the three doublets observed in the origin region likely arise from three different
vibronic transitions.
(1) J. H. Van Vleck, Rev. Mod. Phys. 23, 213 (1951).
(2) W. T. Raynes, J. Chem. Phys. 41, 3020 (1964).
(3) G. Herzberg, Molecular Spectra and Molecular Structure II. Infrared and Raman
Spectra of Polyatomic Molecules (D. Van Nostrand Company, Inc., New York, 1950).
(4) L. H. Spangler, D. W. Pratt, and F. W. Birss, J. Chem. Phys. 85, 3229 (1986).
(5) R. H. Judge and D. C. Moule, J. Mol. Spec. 81, 37 (1980).
(6) J. T. Hougen, Can. J. Phys. 42, 433 (1964).
(7) B. F. Minaev, D. Jonsson, P. Norman, and H. Ågren, Chem. Phys. 194, 19 (1995).
(8) M. Brink, H. Jonson, and C.-H. Ottosson, J. Phys. Chem. A 102, 6513 (1998). The
Gaussian output files containing the structures and normal modes were obtained from C.H. Ottoson.
(9) M. Klessinger and J. Michl, Excited States and Photochemistry of Organic Molecules
(VCH, New York, 1995).