* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Today: Bohr Model - University of Colorado Boulder
James Franck wikipedia , lookup
Molecular Hamiltonian wikipedia , lookup
Particle in a box wikipedia , lookup
Matter wave wikipedia , lookup
X-ray fluorescence wikipedia , lookup
Auger electron spectroscopy wikipedia , lookup
Wave–particle duality wikipedia , lookup
Tight binding wikipedia , lookup
Rutherford backscattering spectrometry wikipedia , lookup
Atomic orbital wikipedia , lookup
X-ray photoelectron spectroscopy wikipedia , lookup
Electron-beam lithography wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Electron configuration wikipedia , lookup
Hydrogen atom wikipedia , lookup
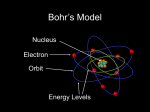
Today: Bohr Model 1. Model for discrete electron orbits in atoms. 2. Prediction of allowed radii from new assumptions. 3. Discrete electronic energies calculated. 4. ‘Hydrogen-like’ ions • HWK 7 due Wed. 10AM. • Week 8 online participation available today • Reading for Friday.: TZ&D Chap. 5.4,5.9, 6.1-6.4. 1 Balmer had a mathematical formula to describe hydrogen spectrum, but no mechanism for why it worked. Hydrogen energy levels Balmer’s formula 656.3 nm 410.3 486.1 434.0 91.19nm λ= 1 1 − 2 2 m n where m=1,2,3 and where n = m+1, m+2 m=1, n=2 2 Rutherford shot alpha particles at atoms figured out: a tiny positive hard core negative charge very far away. • One possible model: atom is like a solar system: electrons circling the nucleus like planets circling the sun… • The problem is that accelerating electrons should radiate light and • spiral into the nucleus: 3 *Elapsed time: ~10-11 seconds Hydrogen atom sim…? QuickTime™ and a TIFF (Uncompressed) decompressor are needed to see this picture. http://phet.colorado.edu 4 Clicker Question Why don’t planets emit radiation and spiral into the sun? A. They do, but very, very slowly. B. Because planets obey quantum mechanics, not classical mechanics. C. Because gravitational forces work differently than electrical forces. D. Because planets are much bigger than electrons. Answer is A. Gravitational radiation is much, much weaker 5 than electromagnetic radiation. Bohr Model • Why Bohr model, – A new model that would predict Balmer lines – & solve the problem of electrons spiraling into the nucleus. • Bohr model has some problems, but still useful. 6 know from experiments Bohr reasoning 1. 1/λnm = R (1/m2 - 1/n2) - Balmer 2. Gravity -1/r2 force gives orbits. Coulomb -ke2/r2 force between electron and proton, So would expect orbits. 3. Classical EM says electron going in circle should radiate energy, spiral in. (accelerating charge radiates) proton + - Bohr hypothesisa. New mix of classical and QM b. Fixed orbits (quant.) and fixed energies c. Classical model (planet analog) 7 If going around in little orbits, important implications from classical physics (review of phys I- planets etc) - + v Basic connections between r, v, and energy! r 8 If going around in little orbits, important implications from classical physics (review of phys I- planets etc) Basic connections between v r, v, and energy! Fcent F = ma= Fcent = ? r (quick memory check) a. -mv + b. -mv2/r c. -v2/r2 d. -mvr e. don’t remember learning anything related to this Ans b) Fcent = -mv2/r Equate to Coulomb force, = kq+ q-/r2, mv2/r =ke2/r2 mv2 = ke2/r k =1/4πε0 (textbook) 9 Nucleus Electron ++ ++ - Higher Energy - Energy levels When electron moves to location further from the nucleus, a. energy of electron decreases because energy is released as positive and negative charges are separated, and there is a decrease in electrostatic potential energy of electron since it is now further away b. energy of electron increases because it takes energy input to separate positive and negative charges, and there is an increase in the electrostatic potential energy of the electron. c. energy of electron increases because it takes energy input to separate positive and negative charges, and there is a 10 decrease in the electrostatic potential energy of the electron. Nucleus Electron ++ ++ - Higher Energy - Energy levels When electron moves to location further from the nucleus, a. energy of electron decreases because energy is released as positive and negative charges are separated, and there is a decrease in electrostatic potential energy of electron since it is now further away b. energy of electron increases because it takes energy input to separate positive and negative charges, and there is an increase in the electrostatic potential energy of the electron. c. energy of electron increases because it takes energy input to separate positive and negative charges, and there is a decrease in the electrostatic potential energy of the electron. (Force on electron is less, but Potential Energy is higher!) 11 Nucleus Electron ++ ++ F- Higher Energy - Energy levels Electron feels force toward nucleus. Must work against that force to move electron farther away, so increase in PE. When electron moves to location further from the nucleus, Answer is b. energy of electron increases because it takes energy input to separate positive and negative charges, and there is an increase in the electrostatic potential energy of the electron. It’s like pushing a boulder out of a ditch (steep at first and shallow later on). 12 So electrons at higher energy levels are further from the nucleus! What does this say about energy? r Fcent v Basic connections between r, v, and energy! mv2 =ke2/r + E = KE + PE = 1/2mv2 +PE 0 distance from proton potential energy PE =? PE = -ke2/r so E = 1/2ke2/r -ke2/r = -1/2ke2/r if know E, know r! if know r, know E! if know r or E, know v! Bohr hypothesis- only certain E levels. Hop down to lowest level, and then stable. 13 Energy (total) levels for electrons 3rd ex. lev. 2nd ex. lev. 1st excited level ground level Bohr- “Electron in orbit with only certain particular energies”. This implies that an electron in Bohr model of hydrogen atom: a. is always at one particular distance from nucleus b. can be at any distance from nucleus. c. can be at certain distances from nucleus corresponding to energy levels it can be in. d. must always go into center where potential energy lowest 14 0 distance from proton potential energy Warning: Bad mix of representations potential energy (curve) total energy (lines) Energy levels for electrons 3rd ex. lev. 2nd ex. lev. 1st excited level ground level Bohr- “Electron in orbit with only certain particular energies”. This implies that an electron in Bohr model of hydrogen atom: a. is always at one particular distance from nucleus b. can be at any distance from nucleus. c. is at certain distances from nucleus corresponding to energy levels it can be in. d. must always go into center where potential energy lowest 15 v r - + Fcent so E = -1/2 ke2/r if know E, know r! if know r, know E! if know r or E, know v! Bohr hypothesis: only certain E levels. e hop down to lowest level, giving off photons when make jump, stable in lowest level. Does not radiate more. 0 distance from proton potential energy But what determines these “special” energies? Complex argument based on idea that at large sizes, electron should radiate classically, differences only at small size. (correspondence principle). Quantized angular momentum L = mvr=nh Predicted special E’s. 16 Bohr calculated special energies. label energy level with n (n = 1, 2, 3, …) involved bunch of constants, h, m, e, c that when combined (see book) give En = -13.6 eV/n2 This then predicts size of jumps between levels. Agreed with observed spectra/Balmer series to four decimal places!! (since E and r, connected, also predicts radius of each orbit. Lowest orbit is “Bohr radius”, ab=0.053 nm, rn =abn2) 17 Review Bohr Model – see book 5.6 Bohr started with 3 basic ideas: Ordinary Classical Mechanics 1. Energy Cons.: E = KE + PE = ½mv2 - ke2/r 2. Centripetal Force: Fcent = mv2/r = ke2/r2 3. Angular Momentum Quantization L = n= Totally new idea: Derived from Correspondence Solve 3 for v ⇒ mvr = n= ⇒ v = n=/mr Principle Sub 3 into 2, solve for r to get rn = n2=2/mke2 = n2aB Hydrogen orbital radii Sub 2 into 1 to get E = -ke2/2r Hydrogen Sub rn into E to get En = -mk2e4/2=2n2 = E1/n2 energies where E1 = -13.6eV = ground state energy of H & aB= =2/mke2 = Bohr radius = size of H in gnd state. 18 Note: k =1/4πε0 (textbook) Successes of Bohr Model • Explains source of Balmer formula and predicts empirical constant from fundamental constants: 1/λ12 = R(1/n22 - 1/n12) ⇔ Ephoton = E1(1/n22 - 1/n12) R = 1/(91.2nm) = mk2e4/4πc=3 • Explains variations in R for different single electron atoms. • Predicts approximate size of hydrogen atom • Explains (sort of) why atoms emit discrete spectral lines • Explains (sort of) why electron doesn’t spiral into nucleus 19 Which of the following principles of classical physics is violated in the Bohr model? A. Opposite charges attract with a force inversely proportional to the square of the distance between them. B. The force on an object is equal to its mass times its acceleration. C. Accelerating charges radiate energy. D. Particles always have a well-defined position and momentum. E. All of the above. Note that both A & B are used in derivation of Bohr model. 20 Bohr model is a weird mix of classical physics and arbitrary rules… • Why is angular momentum quantized yet Newton’s laws still work? • Why don’t electrons radiate when they are in fixed orbitals yet Coulomb’s law still works? • No way to know a priori which rules to keep and which to throw out… 21 What things CAN’T the Bohr model explain? • WHY is angular momentum quantized? • WHY don’t electrons radiate when they are in fixed orbitals? • How does electron know which level to jump to? (i.e. how to predict intensities of spectral lines) • Can’t be generalized to more complex (multielectron) atoms • Shapes of molecular orbits and how bonds work • Can’t explain doublet spectral lines 22 Ideas for how to resolve these problems? 23 L Waves λ1=2L • Physicists at this time may have been confused about atoms, but they understood waves really well. • They understood that for standing waves, boundary conditions mean that waves only have discrete modes. • E.g. guitar strings = node = fixed point that doesn’t move. f1=c/2L λ2=L f2=c/L λ3=2L/3 f3=3c/2L λ4=L/2 f4=2c/L λ5=2L/5 f5=5c/2L λn=2L/n f5=nc/2L … 24 Standing Waves on a Ring Just like standing wave on a string, but now the two ends of the string are joined. What are the restrictions on the wavelength? A. r = λ B. r = nλ n = 1, 2, 3, … C. πr = nλ D. 2πr = nλ E. 2πr = λ/n 25 Standing Waves on a Ring • Answer: D. 2πr = nλ • Circumference = 2πr • To get standing wave on ring: Circumference = nλ Must have integer number of wavelengths to get constructive, not destructive, interference. • n = number of wavelengths 26 deBroglie Waves • deBroglie (French grad student) suggested: maybe electrons are actually little waves going around the nucleus. • This seems plausible because… – Standing waves have quantized frequencies, might be related to quantized energies. – Einstein had shown that light, typically thought of as waves, have particle properties. Might not electrons, typically thought of as particles, have wave properties? 27 deBroglie Waves What is n for electron wave in this picture? 4 3 A. B. C. D. E. 1 1 5 10 10 20 Cannot determine from picture Answer: C. 10 5 2 6 7 9 8 n = number of wavelengths. It is also the number of the energy level En = -13.6/n2. So the wave above corresponds to E10 = -13.6/102 = -0.136eV 28 deBroglie Waves n=1 n=2 n=3 …n=10 = node = fixed point that doesn’t move. 29 deBroglie Waves • If electron orbits are standing waves, there is a relationship between orbital radius and wavelength. • But what is the wavelength of an electron?! • For photons, it was known that photons have (momentum) momentum E= pc= hc/ λ p ⇒ p=h/λ ⇒ λ=h/p λ • deBroglie proposed that this (wavelength) is also true for massive particles (particles w/mass)! • λ=h/p=“deBroglie wavelength” 30 deBroglie Waves Given the deBroglie wavelength (λ=h/p) and the condition for standing waves on a ring (2πr = nλ), what can you say about the angular momentum L of an electron if it is a deBroglie wave? A. B. C. D. E. L = n=/r L = n= L = n=/2 L = 2n=/r L = n=/2r L = angular momentum = pr p = (linear) momentum = mv (Recall: = = h/2π) 31 deBroglie Waves • Substituting the deBroglie wavelength (λ=h/p) into the condition for standing waves (2πr = nλ), gives: 2πr = nh/p • Or, rearranging: pr = nh/2π L = n= • deBroglie EXPLAINS quantization of angular momentum, and therefore EXPLAINS quantization of energy! 32 deBroglie Waves • This is a great story. • But is it true? • If so, why no observations of electron waves? • What would you need to see to believe that this is actually true? • Next: Electron interference! 33 Models of the Atom • Thomson – Plum Pudding – – – – – – Why? Known that negative charges can be removed from atom. – Problem: just a random guess • Rutherford – Solar System – Why? Scattering showed hard core. – Problem: electrons should spiral into nucleus in ~10-11 sec. – + • Bohr – fixed energy levels – Why? Explains spectral lines. – Problem: No reason for fixed energy levels + • deBroglie – electron standing waves – Why? Explains fixed energy levels – Problem: still only works for Hydrogen. + • Schrodinger – quantum wave functions – Why? Explains everything! – Problem: None (except that it’s hard to understand) 34