* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Ch. 21.5-21.9
Electrostatics wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Maxwell's equations wikipedia , lookup
Magnetorotational instability wikipedia , lookup
Friction-plate electromagnetic couplings wikipedia , lookup
History of electrochemistry wikipedia , lookup
Superconducting magnet wikipedia , lookup
Electricity wikipedia , lookup
Magnetic field wikipedia , lookup
Electric machine wikipedia , lookup
Earth's magnetic field wikipedia , lookup
Hall effect wikipedia , lookup
Magnetic nanoparticles wikipedia , lookup
Neutron magnetic moment wikipedia , lookup
Galvanometer wikipedia , lookup
Magnetic monopole wikipedia , lookup
Electromotive force wikipedia , lookup
Superconductivity wikipedia , lookup
Magnetic core wikipedia , lookup
Scanning SQUID microscope wikipedia , lookup
Eddy current wikipedia , lookup
Faraday paradox wikipedia , lookup
Magnetoreception wikipedia , lookup
Magnetohydrodynamics wikipedia , lookup
Electromagnetism wikipedia , lookup
Multiferroics wikipedia , lookup
History of geomagnetism wikipedia , lookup
Force between magnets wikipedia , lookup
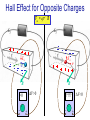
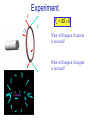
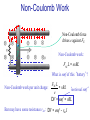
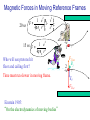
Hall Effect for Opposite Charges Fm = qv ´ B E v E B B V>0 >0 - + v V<0 ???? - + Magnetic Force on a Current-carrying Wire Current: many charges are moving Superposition: add up forces on individual charges Fm = qv ´ B Number of moving charges in short wire: nADl Total force: I Fm = ( nADl ) qv ´ B = ( nqAv ) Dl ´ B Force of a short wire: Fm = IDl ´ B In metals: charges q are negative. Will this equation still work? Exercise Fm = IDl ´ B What is the total force on this wire? What is the magnitude of the force on part L if: I = 10 A B=1T L = 10 cm Fm = ILB = 1 N Experiment F I B Fm = IDl ´ B What will happen if current is reversed? What will happen if magnet is reversed? Forces Between Parallel Wires Definition of 1 Ampere: Ampere is defined as a current at which two very long parallel wires 1 m apart create a force on each other of 2.10-7 N per meter length. From this also follows that 0/(4) = 10-7 T.m/A Forces Between Parallel Wires For long wire: m0 2 I1 B1 = 4p d Magnetic force on lower wire: Fm = IDl ´ B F21 = I 2 LB1 sin 90 o m0 2I1 F21 = I 2 L 4p d Magnetic force on upper wire: m0 2 I 2 B2 = 4p d F12 = I1LB2 sin 90 o m0 2I 2 F12 = I1 L 4p d What if current runs in opposite directions? Electric forces: “likes repel, unlikes attract” Magnetic forces: “likes attract, unlikes repel” Why does the Wire Move? Magnetic force acts only on moving charges Mobile electrons experience magnetic force Atomic cores are not moving – no magnetic force! Atomic cores feel an unbalanced force. Wire moves down! The motion of the wire is an electric side-effect of the magnetic force on the moving electrons. Ee^ = v B Currents Due to Magnetic Forces Metal bar F = qE + qv ´ B Fm = ( -e) v ´ B polarization Static equilibrium: F =0 Fm (-e) E = -(-e)v ´ B E = vB Metal is in static equilibrium: but E 0 inside! What is V ? DV = EL = vBL Currents Due to Magnetic Forces Metal bar Static equilibrium: E = vB DV = EL = vBL Fm How much force do we need to apply to keep the bar moving at constant speed? Does this polarized bar remind you anything we’ve already studied? Non-Coulomb Work Non-Coulomb force drives e against FE Fm Non-Coulomb work: FNC L = evBL What is emf of this ‘battery’? FNC L = vBL ‘motional emf’ Non-Coulomb work per unit charge: e DV = emf = vBL Bar may have some resistance rint: DV = emf - rint I Round-trip Potential What electric fields are produced by the surface charges? Is round trip V zero? E E DV = - ò E × dl Round trip due to these Coulomb electric fields has to be zero. Moving Bar and Energy Conservation P=IV=I(emf) Are we getting something for nothing? Bar – current I: FI F Fm FI = IDl ´ B = -F FI = ILB Work: emf = vBL x W = FDx = ILBDx W Dx = ILB Power: P = Dt Dt Main principle of electric generators: Mechanical power is converted to electric power P = ILBv P = I (emf ) Magnetic Torque on a Magnetic Dipole Moment A current carrying loop has a tendency to twist in magnetic field Compass needle: collection of atomic current loops Fm = IDl ´ B m = IA = Ihw Magnetic Torque: Quantitative Analysis m = Ihw Torque () = distance from the axle (lever arm) times perpendicular component of the force. Fm = IDl ´ B Fm = IwB F^ = IwB sin q æh ö t = 2ç IwB sin q ÷ = IwhB sin q è2 ø t = mB sin q t = m´B Works with loops of any shape! Magnetic Dipole Moment: Potential Energy m = Ihw Calculate amount of work needed to rotate from angle I to f: é æ h öù dE = 2 ê F^ ç dq ÷ ú ë è 2 øû qf æh ö W = DU m = ò 2IwBsin q ç dq ÷ è2 ø q i qf DU m = IwhB ò sinq dq = IwhB [ - cosq ] qi DUm = - m B éë cosq f - cosqi ùû U m = - mB cosq qf qi Potential energy for a magnetic dipole moment Um = -m × B Magnetic Dipole Moment: Potential Energy Potential energy for a magnetic dipole moment Um = -m × B U= min -µB 0 max µB 0 What is the energy difference between the highest and the lowest state? Picture of the U and µ in magnetic field – important in atomic and nuclear physics. Reference Frame m0 qv ´ rˆ B= =0 2 4p r Any magnetic field? m0 qv ´ rˆ B= ¹0 2 4p r charged tape Magnetic Forces in Moving Reference Frames Two protons Electric force: F21,e +e 1 r v F21,m 2 B1 +e v E1 F21,e 1 e2 = q2 E1 = rˆ 2 4pe 0 r Magnetic field: m0 q1v1 ´ rˆ B1 = 4p r 2 Magnetic force: F21,m = q2v2 ´ B1 F21,m m0 e 2 v 2 = q2vB1 = 4p r 2 Magnetic Forces in Moving Reference Frames Electric force: +e 1 r Magnetic force: Ratio: F21,e m0e 0 F21,m m0 e 2 v 2 = 4p r 2 v F21,m 2 B1 +e v E1 1 F21,e 1 e2 = 4pe 0 r 2 ( ) 8 2 = 3 ´ 10 (m/s)2 =c2 it is not accidental! F21,m æ m0 e2v 2 ö æ 1 e 2 ö ÷ ÷ /ç = çç 2 ÷ ç 2 ÷ F21,e è 4p r ø è 4pe 0 r ø F21,m = ( m0e 0 ) v 2 F21,e F21,m v 2 = 2 F21,e c Magnetic Forces in Moving Reference Frames +e 1 r F21,m v 2 = 2 F21,e c v F21,m 2 B1 +e v E1 F21,e Full Lorentz force: For v<<c the magnetic force is much smaller than electric force How can we detect the magnetic force on a current carrying wire? F = F21,e - F21,m downward 1 e2 æ v 2 ö ç1 - 2 ÷÷ = 2 ç 4pe 0 r è c ø Magnetic Forces in Moving Reference Frames 1 e2 æ v 2 ö 20 ns F = 4pe r 2 çç1 - c 2 ÷÷ 0 è ø +e 1 2 1 e 15 ns F = 4pe 0 r 2 Who will see protons hit floor and ceiling first? Time must run slower in moving frame. r v F21,m 2 B1 +e v E1 F21,e Einstein 1905: “On the electrodynamics of moving bodies” Moving Through a Uniform Magnetic Field Blab = 0,0,- B E Fm = qv ´ B Fe = qE v E = Ex ' x E = ' y E = ' y (E y - vBz ) 1- v / c 2 2 - vBz 1- v / c 2 2 E = ' z (E z + vB y ) 1 - v 2 / c2 » vB if v << c The Principle of Relativity There may be different mechanisms for different observers in different reference frames, but all observers can correctly predict what will happen in their own frames, using the same relativistically correct physical laws.