Download electromagnetic induction

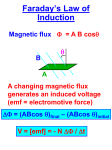
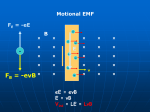
PEI– 1
ELECTROMAGNETIC INDUCTION
6.1
Introduction :
Q. What is electromagnetic induction ?
Solution : The phenomenon in which electric current is generated by varying magnetic fields is
appropriately called electromagnetic induction.
6.2
The Experiments of Faraday and Henry :
Q. Describe one of the experiment carried out by Faraday and Henry to understand electromagnetic
induction ?
OR
Justify the following statement by an experiment carried out by Faraday and Henry : The relative
motion between the magnet and the coil that is responsible for generation (induction) of electric
current in the coil.
Solution :
Figure shows a coil C1 connected to a galvanometer G. When the North-pole of a bar magnet is pushed
towards the coil, the pointer in the galvanometer deflects, indicating the presence of electric current in the
coil. The deflection lasts as long as the bar magnet is in motion. The galvanometer does not show any
deflection when the magnet is held stationary. When the magnet is pulled away from the coil, the
galvanometer shows deflection in the opposite direction, which indicates reversal of the current’s direction.
Moreover, when the Sourth-pole of the bar magnet is moved towards or away from the coil, the deflections
in the galvanometer are opposite to that observed with the North-pole for similar movements. Further, the
deflection (and hence current) is found to be larger when the magnet is pushed towards or pulled away from
the coil faster. Instead, when the bar magnet is held fixed and the coil C1 is moved towards or away from the
magnet, the same effects are observed. It shows that it is the relative motion between the magnet and the
coil that is responsible for generation (induction) of electric current in the coil.
Q. Justify the following statement by an experiment carried out by Faraday and Henry : The relative motion between the coils that induced the electric current.
Solution :
Einstein Classes,
Unit No. 102, 103, Vardhman Ring Road Plaza, Vikas Puri Extn., Outer Ring Road
New Delhi – 110 018, Ph. : 9312629035, 8527112111
PEI – 2
In figure the bar magnet is replaced by a second coil C2 connected to a battery. The steady current in the coil
C2 produces a steady magnetic field. As coil C2 is moved towards the coil C1, the galvanometer shows a
deflection. This indicates that electric current is induced in coil C1. When C2 is moved away, the
galvanometer shows a deflection again, but this time in the opposite direction. The deflection lasts as long
as coil C2 is in motion. When the coil C2 is held fixed and C1 is moved, the same effects are observed. Again,
it is the relative motion between the coils that induced the electric current.
Q. (a) Is there any deflection in galvanometer G if the key K is pressed ? Give reason.
(b) What will be effect if the iron rod is inserted into the coils along their axis ?
Solution : (a) It is observed that the galvanometer shows a momentary deflection when the tapping key K
is pressed. The pointer in the galvanometer returns to zero immediately. If the key is held pressed
continuously, there is no deflection in the galvanometer. When the key is released, a momentary deflection
is observed again, but in the opposite direction.
When the key K is pressed, the current through the coil C2 will change due to which the magnetic flux
linked through the coil C1 will change. That’s why there will be a deflection in the galvanometer G.
(b) The deflection increases dramatically when an iron rod is inserted into the coils along their axis.
6.3
Magnetic Flux :
Q. Define magnetic flux.
Solution :

Magnetic flux through a plane of area A placed in a uniform magnetic field B can be written as


 
 B  B·A  BA cos  where  is an angle between B and A .
Q. What is the SI unit of magnetic flux ? Is it a vector or scalar quantity ?
Solution : The SI unit of magnetic flux is weber (Wb) or tesla meter squared (T m2). Magnetic flux is a
scalar quantity.
6.4
Faraday’s Law of Induction :
Q. State Faraday’s law of electromagnetic induction.
Solution : Faraday’s law of electromagnetic induction is stated : The magnitude of the induced emf in a
circuit is equal to the time rate of change of magnetic flux through the circuit.
Mathematically, the induced emf is given by   
Einstein Classes,
d B
.
dt
Unit No. 102, 103, Vardhman Ring Road Plaza, Vikas Puri Extn., Outer Ring Road
New Delhi – 110 018, Ph. : 9312629035, 8527112111
PEI– 3
The negative sign indicates the direction of  and hence the direction of current in a closed loop.
In the case of a closely wound coil of N turns, change of flux associated with each turn, is the same.
Therefore, the expression for the total induced emf is given by    N
d B
.
dt
Q. Consider Experiment 6.2 (a) What would you do to obtain a large deflection of the
galvanometer ? (b) How would you demonstrate the presence of an induced current in the absence
of a galvanometer ? [NCERT Solved Example 6.1].
Solution : (a) To obtain a large deflection, one or more of the following steps can be taken : (i) Use a rod
made of soft iron inside the coil C2, (ii) Connect the coil to a powerful battery, and (iii) Move the
arrangement rapidly towards the test coil C1.
(b) Replace the galvanometer by a small bulb, the kind one finds in a small torch light. The relative motion
between the two coils will cause the bulb to glow and thus demostrate the presence of an induced current.
Q. A square loop of side 10 cm and resistance 0.5  is placed vertically in the east-west plane. A
uniform magnetic field of 0.10 T is set up across the plane in the north-east direction. The magnetic
field is decreased to zero in 0.70 s at a steady rate. Determine the magnitudes of induced emf and
current during this time-interval. [NCERT Solved Example 6.2]
Solution : 1.0 mV, 2 mA
Q. A circular coil of radius 10 cm, 500 turns and resistance 2  is placed with its plane perpendicular
to the horizontal component of the earth’s magnetic field. It is rotated about its vertical diameter
through 1800 in 0.25 s. Estimate the magnitude of the emf and current induced in the coil. Horizontal
component of the earth’s magnetic field at the place is 3.0 × 10–5T. [NCERT Solved Example 6.3]
Solution : 1.9 × 10–3 A
6.5
Lenz’s Law and Conservation of Energy :
Q. What is Lenz’s Law ?
Solution : The polarity of induced emf is such that it tends to produce a current which opposes the change
in magnetic flux that produced it.
Q. On which conservation principle the Lenz’s Law is based ?
Solution : The Lenz’s Law is based on conservation of energy principle.
Q. Figure shows planar loops of different shapes moving out of or into a region of a magnetic field
which is directed normal to the plane of the loop away from the reader. Determine the direction of
induced current in each loop using Lenz’s law. [NCERT Solved Example 6.4]
Solution : (i) The magnetic flux through the rectangular loop abcd increases, due to the motion of the loop
into the region of magnetic flux. The induced current must flow along the path bcdab so that it opposes the
increasing flux. (ii) Due to the outward motion, magnetic flux through the triangular loop abc decreases
due to which the induced current flows along bacb, so as to oppose the change in flux. (iii) As the magnetic
flux decreases due to motion of the irregular shaped loop abcd out of the region of magnetic field, the
induced current flows along cdabc, so as to oppose change in flux. Note that there is no induced current as
long as the loops are completely inside or outside the region of the magnetic field.
Einstein Classes,
Unit No. 102, 103, Vardhman Ring Road Plaza, Vikas Puri Extn., Outer Ring Road
New Delhi – 110 018, Ph. : 9312629035, 8527112111
PEI – 4
Q. (a) A closed loop is held stationary in the magnetic field between the north and south poles of two
permanent magnets held fixed. Can we hope to generate current in the loop by using very strong
magnets ?
(b) A closed loop moves normal to the constant electric field between the plates of a large capacitor.
Is the current induced in the loop (i) when it is wholly inside the region between the capacitor plates
(ii) when it is partially outside the plates of the capacitor ? The electric field is normal to the plane of
the loop.
(c) A rectangular loop and a circular loop are moving out of a uniform magnetic field to the field-free

region with a constant velocity v . In which loop do you expect the induced emf to be constant during
the passage out of the field region ? The field is normal to the loops.
(d) Predict the polarity of the capacitor in the situation described by this figure
[NCERT Solved Example 6.5]
Solution : (a) No. However strong the magnet may be, current can be induced only by changing the
magnetic flux through the loop. (b) No current is induced in either case. Current can not be induced by
changing the electric flux. (c) The induced emf is expected to be constant only in the case of the rectangular
loop during its passage out of the field region is not constant, hence induced emf will vary accordingly.
(d) The polarity of plate ‘A’ will be positive with respect to plate ‘B’ in the capacitor.
6.6
Motional Electromotive Force :
Q. What is motional emf ?
Solution :
If a conducting rod will move in a magnetic field as shown in figure then an induced emf will be produce
across the ends P and Q of the rod. This induced emf is known as motional emf.
Q. Consider a conducting rod PQ of length l is moving in a magnetic field of magnitude B with
velocity ‘v’ as shown in figure. Derive the expression of induced emf across the ends of the rod.
Einstein Classes,
Unit No. 102, 103, Vardhman Ring Road Plaza, Vikas Puri Extn., Outer Ring Road
New Delhi – 110 018, Ph. : 9312629035, 8527112111
PEI– 5
Solution : Consider any arbitrary charge q in the conductor PQ. When the rod moves with speed v, the

charge will also be moving with speed v in the magnetic field B . The Lorentz force on this charge is qvB
in magnitude, and its direction is towards Q. The work done in moving the charge from P to Q is, W = qvBl.
Since emf is the work done per unit charge,  
W
= Blv..
q
Q. Figure shows a rectangular conductor PQRS in which the conductor PQ is moving with velocity
v in a uniform and time independent magnetic field. Derive the expression for the induced emf
across the end the rod PQ.
Solution : Figure shows a rectangular conductor PQRS in which the conductor PQ is free to move. The rod

PQ is moved towards the left with a constant velocity v as shown in figure. Assume that there is no loss of
energy due to friction. PQRS forms a closed circuit enclosing an area that changes as PQ moves. It is placed

in a uniform magnetic field B which is perpendicular to the plane of this system. If the length PS = x and
RS = l, the magnetic flux B enclosed by the loop PQRS will be B = Blx.
Since x is changing with time, the rate of change of flux B will induce an emf given by :

d B
d
dx

( B lx )  B l
 B lv
dt
dt
dt
Q. A metallic rod of length R is rotated with angular velocity , with one end hinged at the centre and
the other end is at the circumference of a circular metallic ring of radius R, about an axis passing
through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field
of magnitude B parallel to the axis is present everywhere. Derive the expression of induced emf
across the ends of the rod.
Solution :
As the rod is rotated, free electrons in the rod move towards the outer end due to Lorentz force and get
distributed over the ring. Thus, the resulting separation of charges produces an emf across the ends of the
rod. At a certain value of emf, there is no more flow of electrons and a steady state is reached. The
magnitude of the emf generated across a length dr of the rod as it moves at right angles to the magnetic field

R
R


0
0
is given by d = Bvdr. Hence,   d  Bvdr  Br dr 
Einstein Classes,
B R 2
.(  v = r)
2
Unit No. 102, 103, Vardhman Ring Road Plaza, Vikas Puri Extn., Outer Ring Road
New Delhi – 110 018, Ph. : 9312629035, 8527112111
PEI – 6
Q. A metallic rod of 1 m length is rotated with a frequency of 50 rev/s, with one end hinged at the
centre and the other end at the circumference of a circular metallic ring of radius 1 m, about an axis
passing through the centre and perpendicular to the plane of the ring. A constant and uniform
magnetic field of 1 T parallel to the axis is present everywhere. What is the emf between the centre
and the metallic ring ? [NCERT Solved Example 6.6]
Solution : 157 V
Q. A wheel with 10 metallic spokes each 0.5 m long is rotated with a speed of 120 rev/min in a plane
normal to the horizontal component of earth’s magnetic field HE at a place. If HE = 0.4 G at the place,
what is the induced emf between the axle and the rim of the wheel ? Note that 1 G = 10–4 T. Does the
induced emf depend on number of spokes ? [NCERT Solved Example 6.7]
Solution : 6.28 × 10–5 V
6.7
Energy Consideration : A Quantitative Study :
Q. Figure shows a rectangular conductor PQRS in which the conductor PQ is moving with velocity
v in a uniform and time independent magnetic field. Consider the resistance of moving rod PQ is r
i.e., the overall resistance of the loop is r.
(a) find the current in the loop (b) find the force required to move the rod with constant speed ‘v’.
(c) find the power supplied by the external agent to move the rod with speed ‘v’. (d) find the rate at
which the heat will produce ?
Blv

=
. On account of the presence of the magnetic field, there
r
r
 
will be a force on the arm PQ. This force I( l  B) , is directed outwards in the direction opposite to the
Solution : The current I in the loop is I 
velocity of the rod. The magnitude of this force is F  IlB 
B 2l 2 v
.
r
Alternatively, the arm PQ is being pushed with a constant speed v, the power required to do this is,
2
P = Fv =
B2l 2 v2
B 2l 2 v 2
 Blv 
. The rate of heat production is given by, PJ  I 2 r  
.
 r
r
r
 r 
Q. What is the relation between the charge flow through the circuit of resistance r and the change in
magnetic flux ? Derive this relation.
Solution : From Faraday’s law, we have learnt that the magnitude of the induced emf is, |  |
However, |  | Ir 
 B
.
t
 B

.
r . Thus, Q 
t
r
Q. The arm PQ of the rectangular conductor is moved from x = 0, outwards. The uniform magnetic
field is perpendicular to the plane and extends from x = 0 to x = b and is zero for x > b. Only the arm
PQ possesses substantial resistance r. Consider the situation when the arm PQ is pulled outwards
from x = 0 to x = 2b, and is then moved back to x = 0 with constant speed v. Obtain expressions for
the flux, the induced emf, the force necessary to pull the arm and the power dissipated as Joule heat.
Sketch the variation of these quantities with distance. [NCERT Solved Example 6.8]
Einstein Classes,
Unit No. 102, 103, Vardhman Ring Road Plaza, Vikas Puri Extn., Outer Ring Road
New Delhi – 110 018, Ph. : 9312629035, 8527112111
PEI– 7
6.8
Solution : B = Blx
0x<b
= Blb
b  x < 2b
e = –Blv
0x<b
=0
b  x < 2b
F
B2l 2 v
r
0x<b
=0
b  x < 2b
P
B2l 2 v 2
r
0x<b
=0
b  x < 2b
Eddy Currents :
Q. What are eddy currents and how are they produced ?
Solution : When a metallic body is moved in a magnetic field in such a way that the flux through it changes
or is placed in a changing magnetic field, induced currents circulate throughout the volume of the body.
These are called eddy currents.
Q. In what sense are eddy currents considered undesirable in a transformer and how are these
reduced in such a device ?
Solution : Eddy currents dissipate electrical energy in the form of heat. That’s why Eddy currents are
cosidered undesirable in a transformer. Eddy current can be reduced by making rectangular slots in the
conducting plate. These currents are minimised by using lamination of metal to make a metal core. The
laminations are separated by an insulating material like lacquer. The plane of the laminations must be
arranged parallel to the magnetic field, so that they cut across the eddy current paths. This arrangement
reduces the strength of the eddy currents.
Q. Mention application of eddy currents ?
Solution : (i) Magnetic breaking in trains (ii) Electromagnetic damping (iii) Inductance furnace
(iv) Electric power meters.
Q. What is electromagnetic damping and why the oscillation of a copper disc in a magnetic field are
lightly damped ?
Solution : Certain galvanometers have a fixed core made of nonmagnetic metallic material. When the coil
oscillates, the eddy currents generated in the core oppose the motion and bring the coil to rest quickly. This
is known as electromagnetic damping.
The oscillation of a copper disc in a magnetic field are lightly damped due to the generation of eddy current
in the copper disc.
Q. Why do metallic plates use for swing in a magnetic field are punched with holes or slots ?
Solution : To reduce the effect of eddy currents.
Q. What is induction furnace and how does it works ?
Solution : Induction furnace can be used to produce high temperatures and can be utilised to prepare
alloys, by melting the constituent metals. A high frequency alternating current is passed through a coil
which surrounds the metals to be melted. The eddy currents generated in the metals produce high
temperatures sufficient to melt it.
6.9
Inductance :
Q. What is self-inductance ?
Solution : It is also possible that emf is induced in a single isolated coil due to change of flux through the
coil by means of varying the current through the same coil. This phenomenon is called self-induction.
Einstein Classes,
Unit No. 102, 103, Vardhman Ring Road Plaza, Vikas Puri Extn., Outer Ring Road
New Delhi – 110 018, Ph. : 9312629035, 8527112111
PEI – 8
Q. What is coeffieicnt of self-induction ?
OR
What is self-inductance ?
Solution : For a closely wound coil of N turns the flux linkage equals to NB is proportional to the current
in the coil i.e., NB  I  NB = LI. The constant L is called self-inductance or coefficient of self-induction
or simply inductance.
Q. Write down the SI unit of inductance and its dimensions ? Is it a scalar or vector quantity.
Solution : The SI unit of inductance is henry and is denoted by H. It has the dimensions of [ML2T–2A–2]. It
is a scalar quantity.
Q. What is the induced emf developed in an inductor ?
Solution : When the current is varied, the flux linked with the coil also changes and an emf is induced in the
coil. The induced emf is given by   
d( N B )
dI
,   L
.
dt
dt
Thus, the self-induced emf always opposes any change (increase or decrease) of current in the coil.
Q. Derive the expression for self inductance of a long solenoid of cross-sectional area A and length l,
having n turns per unit length. Also express the self-inductance of long solenoid in term of volume V
of solenoid.
Solution : The magnetic field due to a current I flowing in the solenoid is B = µ0nI. The total flux linked
with the solenoid is NB = (nl) (µ0nI) (A) = µ0n2 AlI, where nl is the total number of turns. Thus, the
self-inductance is, L 
N B
= µ0n2 Al. The volume V of the solenoid equals to Al, hence L = µ0n2V.
I
Q. What will be the self inductance of the solenoid (inductor) if a material of relative permeability µr
(like soft iron) will be inserted in the solenoid ? Does the self-inductance increase ?
Solution : If we fill the inside of the solenoid with a material of relative permeability µr (for example soft
iron, which has a high value of relative permiability), then, L = µr µ0 n2 Al.
The self-inductance will be increased due to the insertion of material.
Q. On which factor does inductance depend ?
Solution : The self-inductance depends on its geometry and on the permeability of the medium.
Q. What is back emf ?
Solution : The self-induced emf is also called the back emf as it opposes any change in the currents in a
circuit.
Q. Comment on the following statement : The self-inductance plays the role of inertia.
OR
What is electrical inertia ?
OR
What is the electromagnetic analogue of mass ?
Solution : As an inductor opposes growth and decay of current in the circuit, i.e., the self-inductance has
the role of inertia. It is also known as electromagnetic analogue of mass.
Q. Derive the expression for energy stored in the inductor of inductance L and carrying the current
I.
OR
Derive the work done in establishing the current I in an inductor of inductance L ?
Solution : Work needs to be done against the back emf () in establishing the current. This work done is
stored as magnetic potential energy. For the current I at an instant in a circuit, the rate of work done is
dW
|  | I . If we ignore the resistive losses and consider only inductive effect, then using equation
dt
Einstein Classes,
Unit No. 102, 103, Vardhman Ring Road Plaza, Vikas Puri Extn., Outer Ring Road
New Delhi – 110 018, Ph. : 9312629035, 8527112111
PEI– 9
dW
dI
 LI
. Total amount of work done in establishing the current I is W  dW 
dt
dt

energy required to build up the current I is, W 
1
 L I dI . Thus, the
0
1 2
LI .
2
Q. Define coefficient of mutual inductance of two coils.
A secondary coil of n2 turns per unit length is wound on a long solenoid of area of cross-sectional ‘A’
having a primary coil of n1 turns per unit length. Derive the expression for mutual inductance of the
two coils ?
Solution : Coefficient of mutual inductance :
Consider figure, which shows two long co-axial solenoids each of length l. We denote the radius of the
inner solenoid S1 by r1 and the number of turns per unit length by n1. The corresponding quantities for the
outer solenoid S2 are r2 and n2, respectively. Let N1 and N2 be the total number of turns of coils S1 and S2,
respectively.
When a current I2 is set up through S2, it in turn sets up a magnetic flux through S1. Let us denote it by 1.
The corresponding flux linkage with solenoid S1 is N11 = M12I2.
M12 is called the mutual inductance of solenoid S1 with respect to solenoid S2. It is also referred to as the
coefficient of mutual induction.
Calculation of mutual inductance of two coils :
For these simple co-axial solenoids it is possible to calculate M12. The magnetic field due to the current I2
in S2 is µ0n2I2. The resulting flux linkage with coil S1 is, N11 = (n1l) (r12) (µ0n2I2) = µ0n1n2r12lI2
where n1l is the total number of turns in solenoid S1. Thus M12 = µ0n1n2r12l
We now consider the reverse case. A current I1 is passed through the solenoid S1 and the flux linkage with
coil S2 is, N22 = M21 I1.
M21 is called the mutual inductance of solenoid S2 with respect to solenoid S1.
The flux due to the current I1 in S1 can be assumed to be confied solely inside S1 since the solenoids are very
long. Thus, flux linkage with solenoid S2 is N22 = (n2l) (r12) (µ0n1I1) where n2l is the total number of S2.
Thus M21 = µ0n1n2r12l
Hence, we get M12 = M21 = M (say)
We explained the above example with air as the medium within the solenoids. Instead, if a medium of
relative permeability µr had been present, the mutual inductance would be M = µrµ0n1n2 r12 l.
Q. Does the mutual inductance of a pair of coils depend on their separation as well as there relative
orientation ?
Solution : Yes
Q. How does the mutual inductance of a pair of coils change, when (i) the distance between the coils
is increased ? (ii) the number of turns in each coil is decreased ?
Solution : (i) When the distance between the two coils is increased, mutual inductance of the pair of coils
is decreased because now whole magnetic flux per unit turn of primary coil is not linked with the secondary
Einstein Classes,
Unit No. 102, 103, Vardhman Ring Road Plaza, Vikas Puri Extn., Outer Ring Road
New Delhi – 110 018, Ph. : 9312629035, 8527112111
PEI – 10
µ 0 N1N 2 A
, hence, it is clear that on decreasing number of turns in two
l
coils N1 and N2, the mutual inductance will definitely decreases.
coil. (ii) As mutual inductance M 
Q. Two concentric circular coils, one of small radius r1 and the other of large radius r2, such that
r1 << r2, are placed co-axially with centres coinciding. Obtain the mutual inductance of the
arrangement. [NCERT Solved Example 6.9]
Solution :
µ 0 r12
2r2
Q. (a) Obtain the expression for the magnetic energy stored in a solenoid in terms of magnetic field
B, area A and length l of the solenoid. (b) How does this magnetic energy compare with the
electrostatic energy stored in a capacitor ? [NCERT Solved Example 6.10]
Solution : (a)
6.10
1
B 2 Al
2µ 0
AC Generator :
Q. With the help of neat and labeled diagram, explain the principle, construction and working of an
A.C. generator ?
Solution : Principle of A.C. Generator : Principal of A.C. generator is based on Faraday’s law of
electromagnetic induction. An emf or current in a loop is induced through a change in the loop’s orientation

or a change in its effective area. As the coil rotates in a magnetic field B , the effective area of the loop (the


face perpendicular to the field) is A cos , where  is the angle between A and B . This method of producing a flux change is the principle of operation of a simple ac generator. An ac generator converts mechanical energy into electrical energy.

When the coil is rotated with a constant angular speed  the angle  between the magnetic field vector B

and the area vector A of the coil at any instant t is  = t (assuming  = 00 at t = 0). As a result, the effective
area of the coil exposed to the magnetic field lines changes with time, and the flux at any time t is
B = BA cos  = BA cos t.
From Faraday’s law, the induced emf for the rotating coil of N turns is then,
  N
d B
d
  NBA (cos t ) = NBA sin t
dt
dt
Thus, the instantaneous value of the emf is  = NBA  sin t, where NBA is the maximum value of emf,
which occurs when sin t = ±1. If we denote NBA as 0, then  = 0 sin t.
The direction of the current changes periodically and therefore the current is called alternating current (ac).
Since  = 2, hence induced emf can be written as as  = 0 sin 2 t, where  is the frequency of
revolution of the generator’s coil.
Einstein Classes,
Unit No. 102, 103, Vardhman Ring Road Plaza, Vikas Puri Extn., Outer Ring Road
New Delhi – 110 018, Ph. : 9312629035, 8527112111
PEI– 11
Construction of A.C. generator :
The basic elements of an ac generator are shown in figure. It consists of a coil mounted on a rotor shaft. The
axis of rotation of the coil is perpendicular to the direction of the magnetic field. The coil (called armature)
is mechanically rotatd in the uniform magnetic field by some external means. The rotation of the coil causes
the magnetic flux through it to change, so an emf is induced in the coil. The ends of the coil are connected
to an external circuit by means of slip rings and brushes.
Q. Kamla peddles a stationary bicycle the pedals of the bicycle are attached to a 100 turn coil of area
0.10 m2. The coil rotates at half a revolution per second and it is placed in a uniform magnetic field
of 0.01 T perpendicular to the axis of rotation of the coil. What is the maximum voltage generated in
the coil ? [NCERT Solve Example 6.11]
Solution : 0.314 V
Einstein Classes,
Unit No. 102, 103, Vardhman Ring Road Plaza, Vikas Puri Extn., Outer Ring Road
New Delhi – 110 018, Ph. : 9312629035, 8527112111
PEI – 12
NCERT EXERCISE
6.1
Predict the direction of induced current in the situations described by the following figures (a) to (f).
6.2
Use Lenz’s law to determine the direction of induced current in the situations described by figure.
(a) A wire of irregular shape turning into a circular shape;
(b) A circular loop being deformed into a narrow straight wire.
6.3
A long solenoid with 15 turns per cm has a small loop of area 2.0 cm2 placed inside the solenoid
normal to its axis. If the current carried by the solenoid changes steadily from 2.0 A to 4.0 A in 0.1 s,
what is the induced emf in the loop while the current is changing ?
6.4
(a) A rectangular wire loop of sides 8 cm and 2 cm with a small cut is moving out of region of uniform
magnetic field of magnitude 0.3 T directed normal to the loop. What is the emf developed across the
cut if the velocity of the loop is 1 cm s–1 in a direction normal to the (i) longer side, (ii) shorter side of
the loop ? For how long does the induced voltage last in each case ? (b) Suppose the loop is
stationary but the current feeding the electromagnet that produces the magnetic field is gradually
reduced so that the field decreases from its initial value of 0.3 T at the rate of 0.02 T s–1. If the cut is
joined and the loop has a resistance of 1.6 , how much power is dissipated by the loop as heat ?
What is the source of this power ?
Einstein Classes,
Unit No. 102, 103, Vardhman Ring Road Plaza, Vikas Puri Extn., Outer Ring Road
New Delhi – 110 018, Ph. : 9312629035, 8527112111
PEI– 13
6.5
A 1.0 m long metallic rod is rotated with an angular frequency of 400 rad s–1 about an axis normal to
the rod passing through its one end. The other end of the rod is in contact with a circular metallic
ring. A constant and uniform magnetic field of 0.5 T parallel to the axis everywhere. Calculate the
emf developed between the centre and the ring.
6.6
A circular coil of radius 8.0 cm and 20 turns is rotated about its vertical diameter with an angular
speed of 50 rad s–1 in a uniform horizontal magnetic field of magnitude 3.0 × 10–2T. Obtain the
maximum and average emf induction in the coil. If the coil forms a closed loop of resistance 10,
calculate the maximum value of current in the coil. Calculate the average power loss due to Joule
heating. Where does this power come from ?
6.7
A horizontal straight wire 10 m long extending from east to west is falling with a speed of 5.0 m s–1,
at right angles to the horizontal component of the earth’s magnetic field, 0.30 × 10–4 Wb m–2.
(a)
What is the instantaneous value of the emf induced in the wire ?
(b)
What is the direction of the emf ?
(c)
Which end of the wire is at the higher electrical potential ?
6.8
Current in a circuit falls from 5.0 A to 0.0 A in 0.1 s. If an average emf of 200 V is induced, give an
estimate of the self-inductance of the circuit.
6.9
A pair of adjacent coils has a mutual inductance of 1.5 H. If the current in one coil changes from
0 to 20 A in 0.5 s, what is the change of flux linkage with the other coil ?
6.10
A jet plane is travelling towards west at a speed of 1800 km/h. What is the voltage difference
developed between the ends of the wing having a span of 25 m, if the Earth’s magnetic field at the
location has a magniutude of 5 × 10–4T and the dip angle is 300 ?
ADDITIONAL EXERCISES
6.11
Suppose the loop in Exercise 6.4 is stationary but the current feeding the electromagnet that
produces the magnetic field is gradually reduced so that the field decreases from its initial value of
0.3 T at the rate of 0.02 T s–1. If the cut is joined and the loop has a resistance of 1.6 , how much
power is dissipated by the loop as heat ? What is the source of this power ?
6.12
A square loop of side 12 cm with its sides parallel to X and Y axes is moved with a velocity of
8 cm s–1 in the positive x-direction in an enviroment containing a magnetic field in the positive
z-direction. The field is neither uniform in space nor constant in time. It has a gradient of
10–3Tcm–1 along the negative x-direction (that is it increases by 10–3 T cm–1 as one moves in the
negative x-direction), and it is decreasing in time at the rate of 10–3Ts–1. Determine the direction and
magnitude of the induced current in the loop if its resistance is 4.50 m.
6.13
It is desired to measure the magnitude of field between the poles of a powerful loud speaker magnet.
A small flat search coil of area 2 cm2 with 25 closely wound turns, is positioned normal to the field
direction, and then quickly snatched out of the field region. Equivalently, one can give if a quick 900
turn to bring its plane parallel to the field direction. The total change flown in the coil (measured by
the ballistic galvanometer connected to coil) is 7.5 mC. The combined resistance of the coil and the
galvanometer is 0.50 . Estimate the field strength of magnet.
6.14
Figure shows a metal rod PQ resting on the smooth rails AB and positioned between the poles of a
permanent magnet. The rails, the rod, and the magnetic field are in three mutual perpendicular
directions. A galvanometer G connects the rails through a switch K. Length of the rod = 15 cm,
B = 0.50 T, resistance of the closed loop containing the rod = 9.0 m. Assume the field to be uniform.
(a) Suppose K is open and the rod is moved with a speed of 12 cm s–1 in the direction shown. Give the
polarity and magnitude of the induced emf.
(b) Is there an excess charge built up at the ends of the rods when K is open ? What if K is closed ?
(c) With K open and the rod moving uniformly, there is no net force on the electrons in the rod PQ
even though they do experience magnetic force due to the motion of the rod. Explain.
Einstein Classes,
Unit No. 102, 103, Vardhman Ring Road Plaza, Vikas Puri Extn., Outer Ring Road
New Delhi – 110 018, Ph. : 9312629035, 8527112111
PEI – 14
(d) What is the retarding force on the rod when K is closed ?
(e) How much power is required (by an external agent) to keep the rod moving at the same speed
(=12 cm s–1) when K is closed ? How much power is required when K is open ?
(f) How much power is dissipated as heat in the closed circuit ? What is the source of this power ?
(g) What is the induced emf in the moving rod if the magnetic field is parallel to the rails instead of
being perpendicular ?
6.15
An air-cored solenoid with length 30 cm, area of cross-section 25 cm2 and number of turns 500,
carries a current of 2.5 A. The current is suddenly switched off in a brief time of 10–3s. How much is
the average back emf induced across the ends of the open switch in the circuit ? Ignore the variation
in magnetic field near the ends of the solenoid.
6.16
(a) Obtain an expression for the mutual inductance between a long straight wire and a square loop
of side a shown in figure.
(b) Now assume that the straight wire carries a current of 50 A and the loop is moved to the right
with a constant velocity, v = 10 m/s. Calculate the induced emf in the loop at the instant when
x = 0.2 m. Take a = 0.1 m and assume that the loop has a large resistance.
6.17
A line charge  per unit length is lodged uniformly onto the rim of a wheel of mass M and radius R.
The wheel has light non-conducting spokes and is free to rotate without friction about its axis. A
uniform magnetic field extends over a circular region within the rim. It is given by,

B   B 0 k̂ (r  a; a < R)
= 0 (otherwise)
What is the angular velocity of the wheel after the field is suddenly switched off ?
Einstein Classes,
Unit No. 102, 103, Vardhman Ring Road Plaza, Vikas Puri Extn., Outer Ring Road
New Delhi – 110 018, Ph. : 9312629035, 8527112111
PEI– 15
ANSWERS
6.1
(a) Along qrpq (b) Along prq, along yzx (c) Along yzx (d) Along zyx (e) Along xry (f) No induced
current since field lines lie in the plane of the loop.
6.2
(a) Along adcd (flux through the surface increases during shape change, so induced current
produced opposing flux)
6.3
7.5 × 10–6 V
6.4
(a) 2.4 × 10–4 V, lasting 2s (b) 0.6 × 10–4V, lasting 8 s
6.5
100 V
6.6
0.6 V, 0, 0.06 A, 0.018 W
6.7
(a) 1.5 × 10–3V (b) West to East, (c) Eastern end.
6.8
4.0 H
6.9
30 Wb
6.10
3.1 V
6.11
Induced emf = 8 × 2 × 10–4 × 0.02 = 3.2 × 10–5 V
Induced current = 2 × 10–5 A
Power loss = 6.4 × 10–10 W
Source of this power is the external agent responsible for changing the magnetic field with time.
6.12
2.88 × 10–2 A
6.13
0.75 T
6.15
6.5 V
6.16
e = 1.7 × 10–5V
6.17

Ba 2 
k̂
MR
Einstein Classes,
Unit No. 102, 103, Vardhman Ring Road Plaza, Vikas Puri Extn., Outer Ring Road
New Delhi – 110 018, Ph. : 9312629035, 8527112111
PEI – 16
ADDITIONAL QUESTIONS AND PROBLEMS
Q.
Lenz’s law is the consequence of the law of conservation of energy. Prove this statement or justify it
by an experiment.
A.
According to Lenz’s law, the direction of the induced current is such so as to oppose the cause (i.e., the
change in magnetic flux) that produces it. Lenz’s law is a consequence of the law of conservation of energy.
To show it, let us consider a bar magnet pushed towards a conducting loop. When N-pole moved towards
the loop, the face of the loop facing the north pole develops north polarity as per Lenz’s law so as to oppose
the motion of magnet. Again, when N-pole moves away from the loop, the nearby face develops south
polarity, thus opposing the motion of magnet away from the loop. It means that motion of magnet away
from the loop. It means that motion of magnet is automatically opposed every time. Hence, some work is
tobe done on the magnet to move it towards or away from the loop and this mechanical work is transformed
into electrical energy. Thus, conservation law of energy is strictly followed.
Q.
What is the magnitude of the induced current in the circular loop KLMN of radius r, if the straight
wire PQ carries a steady current of magnitude I A ?
A.
Zero, because magnetic flux linked with the loop remains unchanged.
Q.
Two identical loops, one of copper and another of constanton, are removed from a magnetic field
within the same time interval. In which loop the induced current be greater ?
A.
Induced emf in both the loops is same but induced current is more in copper loop because resistance of
copper loop is lesser than that of constanton loop.
Q.
Why does the acceleration of a magnet falling through a long solenoid decrease ?
A.
As the magnet falls, magnetic flux linked with solenoid changes and an induced current is developed in the
solenoid which opposes the downward motion of magnet. As a result, acceleration of the falling magnet
decreases.
Q.
A magnet is moved in the direction indicated by an arrow between two coils AB and CD as shown in
figure. Suggest the direction of current in each coil.
A.
In coil AB induced current flows in clockwise direction when seen from right side of B. Again in coil CD,
the current appears to flow in clockwise direction when seen from left hand side (or anticlockwise when
seen from right side of end D of coil CD).
Q.
A conducting loop ABC of radius R is moved with a uniform velocity as shown in figure in a uniform

magnetic field B . What is the magnitude of induced emf ?
A.
|| = 2 R Bv.
Einstein Classes,
Unit No. 102, 103, Vardhman Ring Road Plaza, Vikas Puri Extn., Outer Ring Road
New Delhi – 110 018, Ph. : 9312629035, 8527112111
PEI– 17
Q.
Name two devices which have been designed on the principle of mutual induction.
A.
Transformer and induction coil.
Q.
A cylindrical bar magnet is kept along the axis of a circular coil near to it. Will there be any induced
emf at the terminals of the coil, when the magnet is rotated (a) about its own axis, and (b) about an
axis perpendicular to the length of the magnet ?
A.
(a) When the magnet NS is rotated about its own axis, there will be no induced emf at the terminals of the
coil because magnetic flux linked with the coil remains unchanged (b) When the magnet NS is rotated
about an axis perpendicular to the length of the magnet, magnetic flux linked with the coil continuously
changes and hence, an induced emf is set up in the coil.
Q.
12 wires of equal length are connected in the form of a skeleton cube which is moving with a velocity


v in the direction of a magnetic field B . Find the emf in each arm of the cube.
A.
Q.


As in figure v and B are in same direction, hence induced emf in each arm is zero.
The figure shows two identical rectangular loops (1) and (2), placed on a table along with a straight
long current carrying conductor between them.
(i) What will be the directions of the induced current in the loop when they are pulled away from the
conductor with same velocity ?
(ii) Will the emf induced in the two loops be equal ? Justify your answer.
A.
(i) In accordance with Lenz’s law induced current flows in an anticlockwise direction in loop number (1),

but flows in clockwise direction in loop number (2). Due to current I magnetic field B developed around
loop (1) is perpendicular to the plane of paper and pointing outward. On moving the loop away the induced
emf tends to strengthen the magnetic field and hence induced current flows in anticlockwise direction.
Similarly, it can be shown that induced current in loop (2) will flow in clockwise direction.
(ii) Magnitude of induced emf in both the loops will be different. We know that induced emf = B l v.
Although magnitude of B and v is same for both loops but b > a. Hence induced emf in loop (2) 2 = B b v
is move than induced emf in loop (1) 1 = B a v.
Q.
Figure shows a bar magnet M falling under gravity through an air cored coil C. Plot a graph
showing variation of induced emf (E) with time (t).
Einstein Classes,
Unit No. 102, 103, Vardhman Ring Road Plaza, Vikas Puri Extn., Outer Ring Road
New Delhi – 110 018, Ph. : 9312629035, 8527112111
PEI – 18
What does the area enclosed by the E - t curve depict ?
A.
The graph showing variation of induced emf (E) with time (t) is given below in figure
The area enclosed by E-t curve depicts change in flux.
Q.
A.
A bar magnet M is dropped so that it falls vertically through the coil C. The graph obtained for
voltage produced across the coil vs time as shown in figure
(a)
Explain the shape of the graph.
(b)
Why is the negative peak longer than the positive peak ?
As the magnet approaches the coil C, magnetic flux linked with coil increases and an emf is induced in it
which opposes the increase in flux. As speed of magnet increases, magnitude of induced emf increases.
When magnet is fully inside the coil, magnetic flux linked with coil become constant and, hence, induced
emf falls to zero.
As the magnet falls below the coil, magnetic flux of the coil decreases. As a result, an induced emf is set up
which opposes the decrease in flux i.e., which tends to increase the magnetic flux. Thus, induced emf now
is in a direction opposite to that earlier. As velocity of magnet has increased during its fall, the negative
peak of emf is longer than the positive peak. When the magnet has fallen through large distance, magnetic
flux of coil becomes constant and induced emf vanishes.
Q.
A rectangular coil, of N-turns and area of cross-section A, is held in a time varying magnetic field
given by B = B0 sin t with the plane of the coil normal to the magnetic field. Deduce an expression
for the emf induced in the coil.
A.
When a rectangular coil of N-turns and area of cross-section A is held in a magnetic field B with the plane
of the coil normal to the magnetic field, the magnetic flux linked with the coil is given by B = N AB but
B = B0sin t, hence B = N AB0 sin t
 Induced emf in the coil   
Q.
d B
d
  (N A B0 sin t) = – N A B0  cos t.
dt
dt
A rectangular coil of area A having number of turns N is rotated at f revolutions per second in a
uniform magnetic field B, the field being perpendicular to the coil. Prove that the maximum emf
induced in the coil is 2f N B A.
Einstein Classes,
Unit No. 102, 103, Vardhman Ring Road Plaza, Vikas Puri Extn., Outer Ring Road
New Delhi – 110 018, Ph. : 9312629035, 8527112111
PEI– 19
Q.
The given figure, shows an inductor L and resistor R connected in parallel to a battery B through a
switch S. The resistance of R is same as that of the coil that makes L. Two identical bulbs P and Q are
put in each arm of the circuit as shown.
When S is closed, which of the two bulbs will light up earlier ? Justify your answer.
A.
The bulb P joined in the arm containing resistor R will light up earlier when switch S is closed. On closing
the switch, a self-induced back emf is developed in the inductor L in a direction opposite to the emf of
battery B whereas no such emf is induced in resistor R. As a result, bulb P glows up earlier and the bulb Q
glows up a bit late.
Q.
In the arrangement shown in figure above, when switch S is closed, (i) which one of the bulb lights
up earlier, (ii) will the bulbs be equally bright after some time ? Justify your answer.
A.
(i) Bulb P will light up earlier. (ii) Yes, after sometime both the bulbs will glow equally bright. It is because
once the current has reached its maximum value, self-inductanceplays no role. As resistance of both R and
L is same and the bulbs are identical, both will glow will equal brightness.
Q.
Distinguish between self-inductance and mutual inductance.
A.
Self-inductance : (i) Self-induction of a coil is equal to the induced emf set up in it when the current flowing
through it is changing at a unit rate. (ii) Self-inductance of a given coil is fixed.
Mutual inductance : (i) Mutual inductance of a pair of coils is equal to the induced emf set up in one coil
due to a unit rate of change of current in the other coil. (ii) Mutual inductance of a pair of coils changes on
changing their relative orientation.
Q.
A coil A is connected to a voltmeter V and the other coil B to an alternating current source D. If a
large copper sheet C is placed between the two coils, how does the induced emf in the coil A change
due to current in coil B ? Justify your answer.
A.
In the absence of sheet C an induced emf is set up in coil due to mutual induction phenomenon when an
alternating current is passed through coil B.
However, when copper sheet C is placed, eddy currents are set up in the sheet due to change in flux. Thus,
now coil A has a positive effect due to coil B and a negative effect due to eddy currents in C. Consequently,
flux of coil A and hence the induced emf in the coil A is decreased i.e., the reading of voltmeter V is
reduced.
Einstein Classes,
Unit No. 102, 103, Vardhman Ring Road Plaza, Vikas Puri Extn., Outer Ring Road
New Delhi – 110 018, Ph. : 9312629035, 8527112111
PEI – 20
Q.
In the diagram given, a coil B is connected to a low voltage bulb L and placed parallel to another coil
A as shown in figure. Explain the following observations : (i) Bulb lights, and (ii) bulb gets dimmer
if the coil B is moved upwards.
A.
(i) The bulb L joined with coil B lights up due to induced emf produced on account of phenomenon of
mutual induction. Due to flow of an a.c. the magnetic flux of coil A continuously changes and,
consequently, flux of coil B will also change and induced emf will be set up in it.
(ii) If the coil B is moved upward (i.e., away from the coil A), the value of mutual inductance M for the
given pair of coils decrease. As a result, the induced emf in coil B decreases and hence the bulb L gets
dimmer.
Q.
Consider two nearby coils of self-inductance are L1 and L2 and mutual inductance equals to M, then
find the total flux linked through the coil 1 if the current flowing in two coils are I1 and I2
respectively ? Also find the induced emf developed across this coil ?
A.
The flux linked with coil will be the sum of two fluxes which exist independently.
N11 = M11I1 + M12I2 = L1I1 + MI2 ( M111 = L1 and M12 = M)
where M11 represents inductance due to the same coil.
Therefore, using Faraday’s law,  1   M 11
dI 1
dI
 M 12 2 .
dt
dt
M11 is the self-inductance and is written as L1. Therefore,  1   L 1
Einstein Classes,
dI 1
dI
 M 12 2 .
dt
dt
Unit No. 102, 103, Vardhman Ring Road Plaza, Vikas Puri Extn., Outer Ring Road
New Delhi – 110 018, Ph. : 9312629035, 8527112111