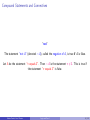Download Logic and Proof - Numeracy Workshop

Please Note
These pdf slides are configured for viewing on a computer screen.
Viewing them on hand-held devices may be difficult as they require a “slideshow”
mode.
Do not try to print them out as there are many more pages than the number of
slides listed at the bottom right of each screen.
Apologies for any inconvenience.
Logic and Proof
Numeracy Workshop
Adrian Dudek, Geoff Coates
Adrian Dudek, Geoff Coates
Logic and Proof
2 / 33
Introduction
These slides give a brief introduction to mathematical logic and methods of proof
Adrian Dudek, Geoff Coates
Logic and Proof
3 / 33
Introduction
These slides give a brief introduction to mathematical logic and methods of proof
Workshop resources: These slides are available online:
www.studysmarter.uwa.edu.au → Numeracy and Maths → Online Resources
Adrian Dudek, Geoff Coates
Logic and Proof
3 / 33
Introduction
These slides give a brief introduction to mathematical logic and methods of proof
Workshop resources: These slides are available online:
www.studysmarter.uwa.edu.au → Numeracy and Maths → Online Resources
Next Workshop: See your Workshop Calendar →
www.studysmarter.uwa.edu.au
Adrian Dudek, Geoff Coates
Logic and Proof
3 / 33
Introduction
These slides give a brief introduction to mathematical logic and methods of proof
Workshop resources: These slides are available online:
www.studysmarter.uwa.edu.au → Numeracy and Maths → Online Resources
Next Workshop: See your Workshop Calendar →
www.studysmarter.uwa.edu.au
Drop-in Study Sessions: Monday, Wednesday, Friday, 10am-12pm, Room 2202, Second
Floor, Social Sciences South Building, every week.
Adrian Dudek, Geoff Coates
Logic and Proof
3 / 33
Introduction
These slides give a brief introduction to mathematical logic and methods of proof
Workshop resources: These slides are available online:
www.studysmarter.uwa.edu.au → Numeracy and Maths → Online Resources
Next Workshop: See your Workshop Calendar →
www.studysmarter.uwa.edu.au
Drop-in Study Sessions: Monday, Wednesday, Friday, 10am-12pm, Room 2202, Second
Floor, Social Sciences South Building, every week.
Email: [email protected]
Adrian Dudek, Geoff Coates
Logic and Proof
3 / 33
Mathematical Statements
Here are some examples of mathematical statements which are written in English:
Adrian Dudek, Geoff Coates
Logic and Proof
4 / 33
Mathematical Statements
Here are some examples of mathematical statements which are written in English:
Adding one to a number always makes the number greater.
Adrian Dudek, Geoff Coates
Logic and Proof
4 / 33
Mathematical Statements
Here are some examples of mathematical statements which are written in English:
Adding one to a number always makes the number greater.
The square root of two is irrational.
Adrian Dudek, Geoff Coates
Logic and Proof
4 / 33
Mathematical Statements
Here are some examples of mathematical statements which are written in English:
Adding one to a number always makes the number greater.
The square root of two is irrational.
Squaring a number always makes it larger.
Adrian Dudek, Geoff Coates
Logic and Proof
4 / 33
Mathematical Statements
Here are some examples of mathematical statements which are written in English:
Adding one to a number always makes the number greater.
The square root of two is irrational.
Squaring a number always makes it larger.
Which of the above are true?
Adrian Dudek, Geoff Coates
Logic and Proof
4 / 33
Mathematical Statements
Here are some examples of mathematical statements which are written in English:
Adding one to a number always makes the number greater. X
The square root of two is irrational.
Squaring a number always makes it larger.
Which of the above are true?
Adrian Dudek, Geoff Coates
Logic and Proof
4 / 33
Mathematical Statements
Here are some examples of mathematical statements which are written in English:
Adding one to a number always makes the number greater. X
The square root of two is irrational. X
Squaring a number always makes it larger.
Which of the above are true?
Adrian Dudek, Geoff Coates
Logic and Proof
4 / 33
Mathematical Statements
Here are some examples of mathematical statements which are written in English:
Adding one to a number always makes the number greater. X
The square root of two is irrational. X
Squaring a number always makes it larger. ×
Which of the above are true?
Adrian Dudek, Geoff Coates
Logic and Proof
4 / 33
Mathematical Statements
The writing and reading maths workshop covered some shorthand notation to replace
common mathematical words and phrases. Here is another one:
Adrian Dudek, Geoff Coates
Logic and Proof
5 / 33
Mathematical Statements
The writing and reading maths workshop covered some shorthand notation to replace
common mathematical words and phrases. Here is another one:
“∀” stands for “for all” or “for every possible value of”.
Adrian Dudek, Geoff Coates
Logic and Proof
5 / 33
Mathematical Statements
The writing and reading maths workshop covered some shorthand notation to replace
common mathematical words and phrases. Here is another one:
“∀” stands for “for all” or “for every possible value of”.
We can use this to shorten written statements:
Adrian Dudek, Geoff Coates
Logic and Proof
5 / 33
Mathematical Statements
The writing and reading maths workshop covered some shorthand notation to replace
common mathematical words and phrases. Here is another one:
“∀” stands for “for all” or “for every possible value of”.
We can use this to shorten written statements:
Adding one to a number always makes the number greater:
Adrian Dudek, Geoff Coates
Logic and Proof
5 / 33
Mathematical Statements
The writing and reading maths workshop covered some shorthand notation to replace
common mathematical words and phrases. Here is another one:
“∀” stands for “for all” or “for every possible value of”.
We can use this to shorten written statements:
Adding one to a number always makes the number greater: ∀x ∈ R
Adrian Dudek, Geoff Coates
Logic and Proof
5 / 33
Mathematical Statements
The writing and reading maths workshop covered some shorthand notation to replace
common mathematical words and phrases. Here is another one:
“∀” stands for “for all” or “for every possible value of”.
We can use this to shorten written statements:
Adding one to a number always makes the number greater: ∀x ∈ R, x + 1 > x.
Adrian Dudek, Geoff Coates
Logic and Proof
5 / 33
Mathematical Statements
The writing and reading maths workshop covered some shorthand notation to replace
common mathematical words and phrases. Here is another one:
“∀” stands for “for all” or “for every possible value of”.
We can use this to shorten written statements:
Adding one to a number always makes the number greater: ∀x ∈ R, x + 1 > x.
The square root of two is irrational:
Adrian Dudek, Geoff Coates
Logic and Proof
5 / 33
Mathematical Statements
The writing and reading maths workshop covered some shorthand notation to replace
common mathematical words and phrases. Here is another one:
“∀” stands for “for all” or “for every possible value of”.
We can use this to shorten written statements:
Adding one to a number always makes the number greater: ∀x ∈ R, x + 1 > x.
√
The square root of two is irrational: 2 ∈ Q
Adrian Dudek, Geoff Coates
Logic and Proof
5 / 33
Mathematical Statements
The writing and reading maths workshop covered some shorthand notation to replace
common mathematical words and phrases. Here is another one:
“∀” stands for “for all” or “for every possible value of”.
We can use this to shorten written statements:
Adding one to a number always makes the number greater: ∀x ∈ R, x + 1 > x.
√
√
/ Q).
The square root of two is irrational: 2 ∈ Q (or 2 ∈
Adrian Dudek, Geoff Coates
Logic and Proof
5 / 33
Mathematical Statements
The writing and reading maths workshop covered some shorthand notation to replace
common mathematical words and phrases. Here is another one:
“∀” stands for “for all” or “for every possible value of”.
We can use this to shorten written statements:
Adding one to a number always makes the number greater: ∀x ∈ R, x + 1 > x.
√
√
/ Q).
The square root of two is irrational: 2 ∈ Q (or 2 ∈
Squaring a number always makes it larger: ∀x ∈ R
Adrian Dudek, Geoff Coates
Logic and Proof
5 / 33
Mathematical Statements
The writing and reading maths workshop covered some shorthand notation to replace
common mathematical words and phrases. Here is another one:
“∀” stands for “for all” or “for every possible value of”.
We can use this to shorten written statements:
Adding one to a number always makes the number greater: ∀x ∈ R, x + 1 > x.
√
√
/ Q).
The square root of two is irrational: 2 ∈ Q (or 2 ∈
Squaring a number always makes it larger: ∀x ∈ R, x 2 > x.
Adrian Dudek, Geoff Coates
Logic and Proof
5 / 33
Compound Statements and Connectives
Statements can be combined, using logical connectives, to form compound statements.
Adrian Dudek, Geoff Coates
Logic and Proof
6 / 33
Compound Statements and Connectives
Statements can be combined, using logical connectives, to form compound statements.
Here we let A and B represent statements.
Adrian Dudek, Geoff Coates
Logic and Proof
6 / 33
Compound Statements and Connectives
Statements can be combined, using logical connectives, to form compound statements.
Here we let A and B represent statements.
“and”
Adrian Dudek, Geoff Coates
Logic and Proof
6 / 33
Compound Statements and Connectives
Statements can be combined, using logical connectives, to form compound statements.
Here we let A and B represent statements.
“and”
The compound statement “A and B” (denoted A ∧ B) is true if A is true and B is true.
Adrian Dudek, Geoff Coates
Logic and Proof
6 / 33
Compound Statements and Connectives
Statements can be combined, using logical connectives, to form compound statements.
Here we let A and B represent statements.
“and”
The compound statement “A and B” (denoted A ∧ B) is true if A is true and B is true.
The statement “It is raining and my socks are wet” is only true if both statements “it is
raining” and “my socks are wet” are true.
Adrian Dudek, Geoff Coates
Logic and Proof
6 / 33
Compound Statements and Connectives
“or”
Adrian Dudek, Geoff Coates
Logic and Proof
7 / 33
Compound Statements and Connectives
“or”
The compound statement “A or B” (denoted A ∨ B) is true if at least one of A or B is
true.
Adrian Dudek, Geoff Coates
Logic and Proof
7 / 33
Compound Statements and Connectives
“or”
The compound statement “A or B” (denoted A ∨ B) is true if at least one of A or B is
true.
The statement “I want to go to the movies or I want to go to the party” is true if one of
the following holds:
Adrian Dudek, Geoff Coates
Logic and Proof
7 / 33
Compound Statements and Connectives
“or”
The compound statement “A or B” (denoted A ∨ B) is true if at least one of A or B is
true.
The statement “I want to go to the movies or I want to go to the party” is true if one of
the following holds:
I want to go to the movies
Adrian Dudek, Geoff Coates
Logic and Proof
7 / 33
Compound Statements and Connectives
“or”
The compound statement “A or B” (denoted A ∨ B) is true if at least one of A or B is
true.
The statement “I want to go to the movies or I want to go to the party” is true if one of
the following holds:
I want to go to the movies
I want to go to the party
Adrian Dudek, Geoff Coates
Logic and Proof
7 / 33
Compound Statements and Connectives
“or”
The compound statement “A or B” (denoted A ∨ B) is true if at least one of A or B is
true.
The statement “I want to go to the movies or I want to go to the party” is true if one of
the following holds:
I want to go to the movies
I want to go to the party
I want to go the movies and I want to go to the party
Adrian Dudek, Geoff Coates
Logic and Proof
7 / 33
Compound Statements and Connectives
“not”
Adrian Dudek, Geoff Coates
Logic and Proof
8 / 33
Compound Statements and Connectives
“not”
The statement “not A” (denoted ∼ A), called the negation of A, is true if A is false.
Adrian Dudek, Geoff Coates
Logic and Proof
8 / 33
Compound Statements and Connectives
“not”
The statement “not A” (denoted ∼ A), called the negation of A, is true if A is false.
Let A be the statement “π equals 3”. Then ∼ A is the statement π 6= 3. This is true if
the statement “π equals 3” is false.
Adrian Dudek, Geoff Coates
Logic and Proof
8 / 33
Compound Statements and Connectives
“implication”
Adrian Dudek, Geoff Coates
Logic and Proof
9 / 33
Compound Statements and Connectives
“implication”
The statement “If A is true, then B is true” (denoted A ⇒ B) is a true statement except
when A is true and B is false.
Adrian Dudek, Geoff Coates
Logic and Proof
9 / 33
Compound Statements and Connectives
“implication”
The statement “If A is true, then B is true” (denoted A ⇒ B) is a true statement except
when A is true and B is false.
Note: If A is false, B could still be true.
Adrian Dudek, Geoff Coates
Logic and Proof
9 / 33
Compound Statements and Connectives
“implication”
The statement “If A is true, then B is true” (denoted A ⇒ B) is a true statement except
when A is true and B is false.
Note: If A is false, B could still be true.
Consider the statement “If I am rich, then I have at least $10”. This is of the form
A ⇒ B, where A is the statement “I am rich” and B is the statement “I have at least
$10”.
Adrian Dudek, Geoff Coates
Logic and Proof
9 / 33
Compound Statements and Connectives
“implication”
The statement “If A is true, then B is true” (denoted A ⇒ B) is a true statement except
when A is true and B is false.
Note: If A is false, B could still be true.
Consider the statement “If I am rich, then I have at least $10”. This is of the form
A ⇒ B, where A is the statement “I am rich” and B is the statement “I have at least
$10”.
Note: If A ⇒ B is true, the reverse implication B ⇒ A may not be.
Adrian Dudek, Geoff Coates
Logic and Proof
9 / 33
Compound Statements and Connectives
“implication”
The statement “If A is true, then B is true” (denoted A ⇒ B) is a true statement except
when A is true and B is false.
Note: If A is false, B could still be true.
Consider the statement “If I am rich, then I have at least $10”. This is of the form
A ⇒ B, where A is the statement “I am rich” and B is the statement “I have at least
$10”.
Note: If A ⇒ B is true, the reverse implication B ⇒ A may not be.
I know lots of people that have at least $10 but are not rich!
Adrian Dudek, Geoff Coates
Logic and Proof
9 / 33
Compound Statements and Connectives
“double implication”
Adrian Dudek, Geoff Coates
Logic and Proof
10 / 33
Compound Statements and Connectives
“double implication”
The statement “A is true if and only if B is true” (denoted A ⇐⇒ B) means A ⇒ B and
B ⇒ A. That is, the statements imply each other!
Adrian Dudek, Geoff Coates
Logic and Proof
10 / 33
Compound Statements and Connectives
“double implication”
The statement “A is true if and only if B is true” (denoted A ⇐⇒ B) means A ⇒ B and
B ⇒ A. That is, the statements imply each other!
Sometimes we say that A and B are equivalent.
Adrian Dudek, Geoff Coates
Logic and Proof
10 / 33
Compound Statements and Connectives
“double implication”
The statement “A is true if and only if B is true” (denoted A ⇐⇒ B) means A ⇒ B and
B ⇒ A. That is, the statements imply each other!
Sometimes we say that A and B are equivalent.
Let A be the statement “x equals zero”, and let B be the statement “x 2 equals zero”.
Adrian Dudek, Geoff Coates
Logic and Proof
10 / 33
Compound Statements and Connectives
“double implication”
The statement “A is true if and only if B is true” (denoted A ⇐⇒ B) means A ⇒ B and
B ⇒ A. That is, the statements imply each other!
Sometimes we say that A and B are equivalent.
Let A be the statement “x equals zero”, and let B be the statement “x 2 equals zero”.
Then we have that A ⇐⇒ B as we have both A ⇒ B and B ⇒ A.
Adrian Dudek, Geoff Coates
Logic and Proof
10 / 33
Exercise
Consider the following two statements:
A : x2 = 9
B : x =3
Which of the following are true?
A⇒B
B⇒A
A ⇐⇒ B
Adrian Dudek, Geoff Coates
Logic and Proof
11 / 33
Exercise
Consider the following two statements:
A : x2 = 9
B : x =3
Which of the following are true?
A⇒B ×
B⇒AX
A ⇐⇒ B ×
Adrian Dudek, Geoff Coates
Logic and Proof
11 / 33
Exercise
Consider the following two statements:
A : x is an even number
B : x + 2 is an even number
Which of the following are true?
A⇒B
B⇒A
A ⇐⇒ B
Adrian Dudek, Geoff Coates
Logic and Proof
12 / 33
Exercise
Consider the following two statements:
A : x is an even number
B : x + 2 is an even number
Which of the following are true?
A⇒B X
B⇒AX
A ⇐⇒ B
Adrian Dudek, Geoff Coates
Logic and Proof
12 / 33
Exercise
Consider the following two statements:
A : x is an even number
B : x + 2 is an even number
Which of the following are true?
A⇒B X
B⇒AX
A ⇐⇒ BX
Adrian Dudek, Geoff Coates
Logic and Proof
12 / 33
The Converse
“converse”
Adrian Dudek, Geoff Coates
Logic and Proof
13 / 33
The Converse
“converse”
B ⇒ A is the converse of A ⇒ B. It’s as easy as reversing the direction of the arrow!
Adrian Dudek, Geoff Coates
Logic and Proof
13 / 33
The Converse
“converse”
B ⇒ A is the converse of A ⇒ B. It’s as easy as reversing the direction of the arrow!
The truth or falsity of a converse can not be inferred from the truth or falsity of the
original statement.
Adrian Dudek, Geoff Coates
Logic and Proof
13 / 33
The Converse
“converse”
B ⇒ A is the converse of A ⇒ B. It’s as easy as reversing the direction of the arrow!
The truth or falsity of a converse can not be inferred from the truth or falsity of the
original statement.
For example,
x = 2 ⇒ x2 = 4
is true, but . . .
Adrian Dudek, Geoff Coates
Logic and Proof
13 / 33
The Converse
“converse”
B ⇒ A is the converse of A ⇒ B. It’s as easy as reversing the direction of the arrow!
The truth or falsity of a converse can not be inferred from the truth or falsity of the
original statement.
For example,
x = 2 ⇒ x2 = 4
is true, but . . . its converse
x2 = 4 ⇒ x = 2
is false, because
Adrian Dudek, Geoff Coates
Logic and Proof
13 / 33
The Converse
“converse”
B ⇒ A is the converse of A ⇒ B. It’s as easy as reversing the direction of the arrow!
The truth or falsity of a converse can not be inferred from the truth or falsity of the
original statement.
For example,
x = 2 ⇒ x2 = 4
is true, but . . . its converse
x2 = 4 ⇒ x = 2
is false, because x could be equal to −2.
Adrian Dudek, Geoff Coates
Logic and Proof
13 / 33
The Contrapositive
“contrapositive”
Adrian Dudek, Geoff Coates
Logic and Proof
14 / 33
The Contrapositive
“contrapositive”
∼ B ⇒∼ A is the contrapositive of A ⇒ B.
Adrian Dudek, Geoff Coates
Logic and Proof
14 / 33
The Contrapositive
“contrapositive”
∼ B ⇒∼ A is the contrapositive of A ⇒ B.
A statement and its contrapositive are logically equivalent. This means that if one is
true, then the other is true!
Adrian Dudek, Geoff Coates
Logic and Proof
14 / 33
The Contrapositive
“contrapositive”
∼ B ⇒∼ A is the contrapositive of A ⇒ B.
A statement and its contrapositive are logically equivalent. This means that if one is
true, then the other is true!
For example,
x = 2 ⇒ x2 = 4
is true, and its contrapositive
Adrian Dudek, Geoff Coates
Logic and Proof
14 / 33
The Contrapositive
“contrapositive”
∼ B ⇒∼ A is the contrapositive of A ⇒ B.
A statement and its contrapositive are logically equivalent. This means that if one is
true, then the other is true!
For example,
x = 2 ⇒ x2 = 4
is true, and its contrapositive
x 2 6= 4 ⇒
Adrian Dudek, Geoff Coates
Logic and Proof
14 / 33
The Contrapositive
“contrapositive”
∼ B ⇒∼ A is the contrapositive of A ⇒ B.
A statement and its contrapositive are logically equivalent. This means that if one is
true, then the other is true!
For example,
x = 2 ⇒ x2 = 4
is true, and its contrapositive
x 2 6= 4 ⇒ x 6= 2
is true.
Adrian Dudek, Geoff Coates
Logic and Proof
14 / 33
The Contrapositive: Example
Consider the statement:
x ≥ 2 ⇒ x2 > 1
The contrapositive of the above is the statement:
Adrian Dudek, Geoff Coates
Logic and Proof
15 / 33
The Contrapositive: Example
Consider the statement:
x ≥ 2 ⇒ x2 > 1
The contrapositive of the above is the statement:
x2 ≤ 1
Adrian Dudek, Geoff Coates
Logic and Proof
15 / 33
The Contrapositive: Example
Consider the statement:
x ≥ 2 ⇒ x2 > 1
The contrapositive of the above is the statement:
x2 ≤ 1 ⇒ x < 2
Both are true.
Adrian Dudek, Geoff Coates
Logic and Proof
15 / 33
Necessary and Sufficient Conditions
If the statement A ⇒ B is true then we say “A is a sufficient condition for B”, i.e. the
truth of A is sufficient to guarantee that B is true.
Adrian Dudek, Geoff Coates
Logic and Proof
16 / 33
Necessary and Sufficient Conditions
If the statement A ⇒ B is true then we say “A is a sufficient condition for B”, i.e. the
truth of A is sufficient to guarantee that B is true.
Example: “I am rich” ⇒ “I have at least $10” so if “I am rich” (A) is true, it guarantees
that “I have at least $10” (B).
Adrian Dudek, Geoff Coates
Logic and Proof
16 / 33
Necessary and Sufficient Conditions
If the statement A ⇒ B is true then we say “A is a sufficient condition for B”, i.e. the
truth of A is sufficient to guarantee that B is true.
Example: “I am rich” ⇒ “I have at least $10” so if “I am rich” (A) is true, it guarantees
that “I have at least $10” (B).
We also say that “B is a necessary condition for A”, i.e., if B is false then A is false.
Adrian Dudek, Geoff Coates
Logic and Proof
16 / 33
Necessary and Sufficient Conditions
If the statement A ⇒ B is true then we say “A is a sufficient condition for B”, i.e. the
truth of A is sufficient to guarantee that B is true.
Example: “I am rich” ⇒ “I have at least $10” so if “I am rich” (A) is true, it guarantees
that “I have at least $10” (B).
We also say that “B is a necessary condition for A”, i.e., if B is false then A is false.
Example: If “I have at least $10” (B) is false, then I can’t be rich (A).
Adrian Dudek, Geoff Coates
Logic and Proof
16 / 33
Necessary and Sufficient Conditions
If the statement A ⇒ B is true then we say “A is a sufficient condition for B”, i.e. the
truth of A is sufficient to guarantee that B is true.
Example: “I am rich” ⇒ “I have at least $10” so if “I am rich” (A) is true, it guarantees
that “I have at least $10” (B).
We also say that “B is a necessary condition for A”, i.e., if B is false then A is false.
Example: If “I have at least $10” (B) is false, then I can’t be rich (A).
If the statement A ⇐⇒ B is true, then we say that “A is necessary and sufficient for B”.
Adrian Dudek, Geoff Coates
Logic and Proof
16 / 33
Proof
Some might say that mathematics is a “toolkit of truths”.
Adrian Dudek, Geoff Coates
Logic and Proof
17 / 33
Proof
Some might say that mathematics is a “toolkit of truths”.
Research in mathematics consists of increasing the number of tools in our toolkit.
Adrian Dudek, Geoff Coates
Logic and Proof
17 / 33
Proof
Some might say that mathematics is a “toolkit of truths”.
Research in mathematics consists of increasing the number of tools in our toolkit.
The way that we prove new tools, is to show that they are implications of tools which are
already in our toolkit.
Adrian Dudek, Geoff Coates
Logic and Proof
17 / 33
Proof
Some might say that mathematics is a “toolkit of truths”.
Research in mathematics consists of increasing the number of tools in our toolkit.
The way that we prove new tools, is to show that they are implications of tools which are
already in our toolkit.
There are two main kinds of tool: axioms and theorems.
Adrian Dudek, Geoff Coates
Logic and Proof
17 / 33
Axioms
Axioms are statements that are simply accepted as being true without the need for proof.
This is because they are so fundamental that we feel everyone must accept them.
Adrian Dudek, Geoff Coates
Logic and Proof
18 / 33
Axioms
Axioms are statements that are simply accepted as being true without the need for proof.
This is because they are so fundamental that we feel everyone must accept them.
Here are some examples:
Adrian Dudek, Geoff Coates
Logic and Proof
18 / 33
Axioms
Axioms are statements that are simply accepted as being true without the need for proof.
This is because they are so fundamental that we feel everyone must accept them.
Here are some examples:
Euclid’s First Axiom: There is only one straight line that can be drawn to join two
specific points in space.
Adrian Dudek, Geoff Coates
Logic and Proof
18 / 33
Axioms
Axioms are statements that are simply accepted as being true without the need for proof.
This is because they are so fundamental that we feel everyone must accept them.
Here are some examples:
Euclid’s First Axiom: There is only one straight line that can be drawn to join two
specific points in space.
Well Ordering Principle: Every non-empty set of positive integers contains a smallest
element.
Adrian Dudek, Geoff Coates
Logic and Proof
18 / 33
Theorems
Theorems are statements that can be proved to be true using accepted definitions,
axioms, and other already proven theorems.
Adrian Dudek, Geoff Coates
Logic and Proof
19 / 33
Theorems
Theorems are statements that can be proved to be true using accepted definitions,
axioms, and other already proven theorems.
The truth of the theorem is arrived at by reasoning from other accepted truths.
Adrian Dudek, Geoff Coates
Logic and Proof
19 / 33
Deductive Proofs using Algebra
Look what happens when we multiply two even numbers together:
4 × 6 = 24
Adrian Dudek, Geoff Coates
Logic and Proof
20 / 33
Deductive Proofs using Algebra
Look what happens when we multiply two even numbers together:
4 × 6 = 24
8 × 2 = 16
Adrian Dudek, Geoff Coates
Logic and Proof
20 / 33
Deductive Proofs using Algebra
Look what happens when we multiply two even numbers together:
4 × 6 = 24
8 × 2 = 16
4 × 4 = 16
Adrian Dudek, Geoff Coates
Logic and Proof
20 / 33
Deductive Proofs using Algebra
Look what happens when we multiply two even numbers together:
4 × 6 = 24
8 × 2 = 16
4 × 4 = 16
40 × 8 = 320
Adrian Dudek, Geoff Coates
Logic and Proof
20 / 33
Deductive Proofs using Algebra
Look what happens when we multiply two even numbers together:
4 × 6 = 24
8 × 2 = 16
4 × 4 = 16
40 × 8 = 320
We always seem to get an even number.
Adrian Dudek, Geoff Coates
Logic and Proof
20 / 33
Deductive Proofs using Algebra
Look what happens when we multiply two even numbers together:
4 × 6 = 24
8 × 2 = 16
4 × 4 = 16
40 × 8 = 320
We always seem to get an even number.
However, we can not conclude that the statement “the product of any two even numbers
is even” is a true statement, simply because we have seen a few examples.
Adrian Dudek, Geoff Coates
Logic and Proof
20 / 33
Deductive Proofs using Algebra
Look what happens when we multiply two even numbers together:
4 × 6 = 24
8 × 2 = 16
4 × 4 = 16
40 × 8 = 320
We always seem to get an even number.
However, we can not conclude that the statement “the product of any two even numbers
is even” is a true statement, simply because we have seen a few examples.
We need to prove this theorem completely. This means that we have to present a
convincing argument.
Adrian Dudek, Geoff Coates
Logic and Proof
20 / 33
Deductive Proofs using Algebra
We want to show that for any two even numbers we choose, their product is also even.
Adrian Dudek, Geoff Coates
Logic and Proof
21 / 33
Deductive Proofs using Algebra
We want to show that for any two even numbers we choose, their product is also even.
However, we don’t want to write out every single choice of two even numbers as this is
impossible!
Adrian Dudek, Geoff Coates
Logic and Proof
21 / 33
Deductive Proofs using Algebra
We want to show that for any two even numbers we choose, their product is also even.
However, we don’t want to write out every single choice of two even numbers as this is
impossible!
Instead, we use expressions which represent arbitrary even numbers.
Adrian Dudek, Geoff Coates
Logic and Proof
21 / 33
Deductive Proofs using Algebra
We want to show that for any two even numbers we choose, their product is also even.
However, we don’t want to write out every single choice of two even numbers as this is
impossible!
Instead, we use expressions which represent arbitrary even numbers.
By definition, even numbers are multiples of two, that is, any even number is the product
of 2 and some other integer.
Adrian Dudek, Geoff Coates
Logic and Proof
21 / 33
Deductive Proofs using Algebra
We want to show that for any two even numbers we choose, their product is also even.
However, we don’t want to write out every single choice of two even numbers as this is
impossible!
Instead, we use expressions which represent arbitrary even numbers.
By definition, even numbers are multiples of two, that is, any even number is the product
of 2 and some other integer.
Hence, we can represent an even number by the expression 2n, where n is an integer.
Adrian Dudek, Geoff Coates
Logic and Proof
21 / 33
Proof: even x even = even
Here is our proof. Take two even numbers:
2n, 2m
Adrian Dudek, Geoff Coates
Logic and Proof
22 / 33
Proof: even x even = even
Here is our proof. Take two even numbers:
2n, 2m
Multiply them together:
(2n)(2m)
Adrian Dudek, Geoff Coates
Logic and Proof
22 / 33
Proof: even x even = even
Here is our proof. Take two even numbers:
2n, 2m
Multiply them together:
(2n)(2m)
We can simplify and express the above product in a clever way!
(2n)(2m) = 4nm
Adrian Dudek, Geoff Coates
Logic and Proof
22 / 33
Proof: even x even = even
Here is our proof. Take two even numbers:
2n, 2m
Multiply them together:
(2n)(2m)
We can simplify and express the above product in a clever way!
(2n)(2m) = 4nm = 2(2nm)
Adrian Dudek, Geoff Coates
Logic and Proof
22 / 33
Proof: even x even = even
Here is our proof. Take two even numbers:
2n, 2m
Multiply them together:
(2n)(2m)
We can simplify and express the above product in a clever way!
(2n)(2m) = 4nm = 2(2nm)
But 2(2nm) is really just the product of 2 and an integer (ie. 2nm)! So this product is
clearly even!
Adrian Dudek, Geoff Coates
Logic and Proof
22 / 33
Proof: even x even = even
Here is our proof. Take two even numbers:
2n, 2m
Multiply them together:
(2n)(2m)
We can simplify and express the above product in a clever way!
(2n)(2m) = 4nm = 2(2nm)
But 2(2nm) is really just the product of 2 and an integer (ie. 2nm)! So this product is
clearly even!
Note: We usually denote the end of a proof with a box.
Adrian Dudek, Geoff Coates
Logic and Proof
22 / 33
Proof: even x even = even
Here is our proof. Take two even numbers:
2n, 2m
Multiply them together:
(2n)(2m)
We can simplify and express the above product in a clever way!
(2n)(2m) = 4nm = 2(2nm)
But 2(2nm) is really just the product of 2 and an integer (ie. 2nm)! So this product is
clearly even! Note: We usually denote the end of a proof with a box.
Adrian Dudek, Geoff Coates
Logic and Proof
22 / 33
Proof: odd + odd = even
Let’s prove that the sum of two odd numbers is even. Here is our proof.
Adrian Dudek, Geoff Coates
Logic and Proof
23 / 33
Proof: odd + odd = even
Let’s prove that the sum of two odd numbers is even. Here is our proof.
Take two odd numbers:
2n + 1, 2m + 1
Adrian Dudek, Geoff Coates
Logic and Proof
23 / 33
Proof: odd + odd = even
Let’s prove that the sum of two odd numbers is even. Here is our proof.
Take two odd numbers:
2n + 1, 2m + 1
Add them together:
2n + 1 + 2m + 1
Adrian Dudek, Geoff Coates
Logic and Proof
23 / 33
Proof: odd + odd = even
Let’s prove that the sum of two odd numbers is even. Here is our proof.
Take two odd numbers:
2n + 1, 2m + 1
Add them together:
2n + 1 + 2m + 1
We can simplify and express the above in the same clever way:
2n + 1 + 2m + 1 = 2n + 2m + 2
Adrian Dudek, Geoff Coates
Logic and Proof
23 / 33
Proof: odd + odd = even
Let’s prove that the sum of two odd numbers is even. Here is our proof.
Take two odd numbers:
2n + 1, 2m + 1
Add them together:
2n + 1 + 2m + 1
We can simplify and express the above in the same clever way:
2n + 1 + 2m + 1 = 2n + 2m + 2 = 2(n + m + 1)
Adrian Dudek, Geoff Coates
Logic and Proof
23 / 33
Proof: odd + odd = even
Let’s prove that the sum of two odd numbers is even. Here is our proof.
Take two odd numbers:
2n + 1, 2m + 1
Add them together:
2n + 1 + 2m + 1
We can simplify and express the above in the same clever way:
2n + 1 + 2m + 1 = 2n + 2m + 2 = 2(n + m + 1)
We have managed to write the sum of two odd numbers as a number which is a multiple
of 2! So the sum of two odd numbers must be an even number.
Adrian Dudek, Geoff Coates
Logic and Proof
23 / 33
Proof: odd + odd = even
Let’s prove that the sum of two odd numbers is even. Here is our proof.
Take two odd numbers:
2n + 1, 2m + 1
Add them together:
2n + 1 + 2m + 1
We can simplify and express the above in the same clever way:
2n + 1 + 2m + 1 = 2n + 2m + 2 = 2(n + m + 1)
We have managed to write the sum of two odd numbers as a number which is a multiple
of 2! So the sum of two odd numbers must be an even number. Adrian Dudek, Geoff Coates
Logic and Proof
23 / 33
Structure of algebraic deductive proof
Theorem: If statement(s) is/are true, show that statement is true.
Adrian Dudek, Geoff Coates
Logic and Proof
24 / 33
Structure of algebraic deductive proof
Theorem: If statement(s) is/are true, show that statement is true.
Proof: statement(s) given
Structure of algebraic deductive proof
Theorem: If statement(s) is/are true, show that statement is true.
Proof: statement(s) given
statement to be proved
Structure of algebraic deductive proof
Theorem: If statement(s) is/are true, show that statement is true.
Proof: statement(s) given
clever, legal steps
statement to be proved
Structure of algebraic deductive proof
Theorem: If statement(s) is/are true, show that statement is true.
Proof: statement(s) given
clever, legal steps
clever, legal steps
statement to be proved
Adrian Dudek, Geoff Coates
Logic and Proof
24 / 33
Structure of algebraic deductive proof: example
(This example involves matrices and is similar to proofs in MATH1001.)
Theorem: If A is a symmetric, invertible matrix then A−1 is also symmetric.
A−1
Adrian Dudek, Geoff Coates
T
Express the red and blue phrases algebraically.
Logic and Proof
25 / 33
Structure of algebraic deductive proof: example
(This example involves matrices and is similar to proofs in MATH1001.)
Theorem: If A is a symmetric, invertible matrix then A−1 is also symmetric.
Proof:
A−1
Adrian Dudek, Geoff Coates
T
Express the red and blue phrases algebraically.
Logic and Proof
25 / 33
Structure of algebraic deductive proof: example
(This example involves matrices and is similar to proofs in MATH1001.)
Theorem: If A is a symmetric, invertible matrix then A−1 is also symmetric.
Proof: We know
A−1
Adrian Dudek, Geoff Coates
T
Express the red and blue phrases algebraically.
Logic and Proof
25 / 33
Structure of algebraic deductive proof: example
(This example involves matrices and is similar to proofs in MATH1001.)
Theorem: If A is a symmetric, invertible matrix then A−1 is also symmetric.
Proof: We know A is symmetric
A−1
Adrian Dudek, Geoff Coates
T
Express the red and blue phrases algebraically.
Logic and Proof
25 / 33
Structure of algebraic deductive proof: example
(This example involves matrices and is similar to proofs in MATH1001.)
Theorem: If A is a symmetric, invertible matrix then A−1 is also symmetric.
Proof: We know A is symmetric and A is invertible
A−1
Adrian Dudek, Geoff Coates
T
Express the red and blue phrases algebraically.
Logic and Proof
25 / 33
Structure of algebraic deductive proof: example
(This example involves matrices and is similar to proofs in MATH1001.)
Theorem: If A is a symmetric, invertible matrix then A−1 is also symmetric.
Proof: We know A is symmetric and A is invertible
A−1 is symmetric
A
−1 T
Adrian Dudek, Geoff Coates
Express the red and blue phrases algebraically.
Logic and Proof
25 / 33
Structure of algebraic deductive proof: example
(This example involves matrices and is similar to proofs in MATH1001.)
Theorem: If A is a symmetric, invertible matrix then A−1 is also symmetric.
Proof: We know A is symmetric and A is invertible
clever, legal steps
A−1 is symmetric
Proofs are hard because “clever” steps may be hard to spot. Here are some tips. A−1
Adrian Dudek, Geoff Coates
Logic and Proof
T
25 / 33
Structure of algebraic deductive proof: example
(This example involves matrices and is similar to proofs in MATH1001.)
Theorem: If A is a symmetric, invertible matrix then A−1 is also symmetric.
Proof: We know A is symmetric and A is invertible
A−1 is symmetric
T
T
A−1 Tip: Express the red and blue phrases algebraically. A−1
Adrian Dudek, Geoff Coates
Logic and Proof
25 / 33
Structure of algebraic deductive proof: example
(This example involves matrices and is similar to proofs in MATH1001.)
Theorem: If A is a symmetric, invertible matrix then A−1 is also symmetric.
Proof: We know A is symmetric and A is invertible
AT = A
A−1 is symmetric
T
T
A−1 Tip: Express the red and blue phrases algebraically. A−1
Adrian Dudek, Geoff Coates
Logic and Proof
25 / 33
Structure of algebraic deductive proof: example
(This example involves matrices and is similar to proofs in MATH1001.)
Theorem: If A is a symmetric, invertible matrix then A−1 is also symmetric.
Proof: We know A is symmetric and A is invertible
AT = A
and
A−1 exists
A−1 is symmetric
T
T
A−1 Tip: Express the red and blue phrases algebraically. A−1
Adrian Dudek, Geoff Coates
Logic and Proof
25 / 33
Structure of algebraic deductive proof: example
(This example involves matrices and is similar to proofs in MATH1001.)
Theorem: If A is a symmetric, invertible matrix then A−1 is also symmetric.
Proof: We know A is symmetric and A is invertible
AT = A
and
A−1 exists
A−1
T
= A−1
A−1 is symmetric
T
T
A−1 Tip: Express the red and blue phrases algebraically. A−1
Adrian Dudek, Geoff Coates
Logic and Proof
25 / 33
Structure of algebraic deductive proof: example
(This example involves matrices and is similar to proofs in MATH1001.)
Theorem: If A is a symmetric, invertible matrix then A−1 is also symmetric.
Proof: We know A is symmetric and A is invertible
AT = A
and
A−1 exists
A−1
T
= A−1
A−1 is symmetric
T
T
A−1 We need to start with an equation involving A−1 . . . A−1
Adrian Dudek, Geoff Coates
Logic and Proof
25 / 33
Structure of algebraic deductive proof: example
(This example involves matrices and is similar to proofs in MATH1001.)
Theorem: If A is a symmetric, invertible matrix then A−1 is also symmetric.
Proof: We know A is symmetric and A is invertible
AT = A
and
⇒
A−1 exists
AA−1 = I
A−1
T
(from defn of inverse)
= A−1
A−1 is symmetric
T
T
A−1 We need to start with an equation involving A−1 . . . A−1
Adrian Dudek, Geoff Coates
Logic and Proof
25 / 33
Structure of algebraic deductive proof: example
(This example involves matrices and is similar to proofs in MATH1001.)
Theorem: If A is a symmetric, invertible matrix then A−1 is also symmetric.
Proof: We know A is symmetric and A is invertible
AT = A
and
⇒
A−1 exists
AA−1 = I
A−1
T
(from defn of inverse)
= A−1
A−1 is symmetric
T
T
A−1 Now to get transpose involved . . . A−1
Adrian Dudek, Geoff Coates
Logic and Proof
25 / 33
Structure of algebraic deductive proof: example
(This example involves matrices and is similar to proofs in MATH1001.)
Theorem: If A is a symmetric, invertible matrix then A−1 is also symmetric.
Proof: We know A is symmetric and A is invertible
AT = A
and
⇒
⇒
A−1 exists
AA−1 = I
(from defn of inverse)
T
AA−1 = (I )T = I
(transpose both sides)
A−1
T
= A−1
A−1 is symmetric
T
T
A−1 Now to get transpose involved . . . A−1
Adrian Dudek, Geoff Coates
Logic and Proof
25 / 33
Structure of algebraic deductive proof: example
(This example involves matrices and is similar to proofs in MATH1001.)
Theorem: If A is a symmetric, invertible matrix then A−1 is also symmetric.
Proof: We know A is symmetric and A is invertible
AT = A
and
⇒
⇒
A−1 exists
AA−1 = I
(from defn of inverse)
T
AA−1 = (I )T = I
(transpose both sides)
A−1
T
= A−1
A−1 is symmetric
T
We need to get an A−1 term.
Adrian Dudek, Geoff Coates
Logic and Proof
25 / 33
Structure of algebraic deductive proof: example
(This example involves matrices and is similar to proofs in MATH1001.)
Theorem: If A is a symmetric, invertible matrix then A−1 is also symmetric.
Proof: We know A is symmetric and A is invertible
AT = A
and
⇒
⇒
⇒
A−1 exists
AA−1 = I
(from defn of inverse)
T
AA−1 = (I )T = I
(transpose both sides)
T
A−1 AT = I
(a property of transpose)
A−1
T
= A−1
A−1 is symmetric
T
We need to get an A−1 term.
Adrian Dudek, Geoff Coates
Logic and Proof
25 / 33
Structure of algebraic deductive proof: example
(This example involves matrices and is similar to proofs in MATH1001.)
Theorem: If A is a symmetric, invertible matrix then A−1 is also symmetric.
Proof: We know A is symmetric and A is invertible
AT = A
and
⇒
⇒
⇒
⇒
A−1 exists
AA−1 = I
(from defn of inverse)
T
AA−1 = (I )T = I
(transpose both sides)
T
A−1 AT = I
(a property of transpose)
T
A−1 A = I
(known property of A)
A−1
T
= A−1
A−1 is symmetric
A
−1 T
Adrian Dudek, Geoff Coates
Express the red and blue phrases algebraically.
Logic and Proof
25 / 33
Structure of algebraic deductive proof: example
(This example involves matrices and is similar to proofs in MATH1001.)
Theorem: If A is a symmetric, invertible matrix then A−1 is also symmetric.
Proof: We know A is symmetric and A is invertible
AT = A
and
⇒
⇒
⇒
⇒
⇒
A−1 exists
AA−1 = I
(from defn of inverse)
T
AA−1 = (I )T = I
(transpose both sides)
T
A−1 AT = I
(a property of transpose)
T
A−1 A = I
(known property of A)
T
A−1 is the inverse of A by defn of inverse
T
A−1 = A−1
A−1 is symmetric
A
−1 T
Adrian Dudek, Geoff Coates
Express the red and blue phrases algebraically.
Logic and Proof
25 / 33
Structure of algebraic deductive proof: example
(This example involves matrices and is similar to proofs in MATH1001.)
Theorem: If A is a symmetric, invertible matrix then A−1 is also symmetric.
Proof: We know A is symmetric and A is invertible
AT = A
and
⇒
⇒
⇒
⇒
⇒
⇒
A−1 exists
AA−1 = I
(from defn of inverse)
T
AA−1 = (I )T = I
(transpose both sides)
T
A−1 AT = I
(a property of transpose)
T
A−1 A = I
(known property of A)
T
A−1 is the inverse of A by defn of inverse
T
A−1 = A−1
A−1 is symmetric
A
−1 T
Adrian Dudek, Geoff Coates
Express the red and blue phrases algebraically.
Logic and Proof
25 / 33
Structure of algebraic deductive proof: example
(This example involves matrices and is similar to proofs in MATH1001.)
Theorem: If A is a symmetric, invertible matrix then A−1 is also symmetric.
Proof: We know A is symmetric and A is invertible
AT = A
and
⇒
AA−1 = I
(from defn of inverse)
T
AA−1 = (I )T = I
(transpose both sides)
T
A−1 AT = I
(a property of transpose)
T
A−1 A = I
(known property of A)
T
A−1 is the inverse of A by defn of inverse
T
A−1 = A−1
∴
A−1 is symmetric
⇒
⇒
⇒
⇒
⇒
A
−1 T
Adrian Dudek, Geoff Coates
A−1 exists
Express the red and blue phrases algebraically.
Logic and Proof
25 / 33
Structure of algebraic deductive proof: example
(This example involves matrices and is similar to proofs in MATH1001.)
Theorem: If A is a symmetric, invertible matrix then A−1 is also symmetric.
Proof: We know A is symmetric and A is invertible
AT = A
and
⇒
AA−1 = I
(from defn of inverse)
T
AA−1 = (I )T = I
(transpose both sides)
T
A−1 AT = I
(a property of transpose)
T
A−1 A = I
(known property of A)
T
A−1 is the inverse of A by defn of inverse
T
A−1 = A−1
∴
A−1 is symmetric ⇒
⇒
⇒
⇒
⇒
A
−1 T
Adrian Dudek, Geoff Coates
A−1 exists
Express the red and blue phrases algebraically.
Logic and Proof
25 / 33
Proof or Counterexample
To prove that a statement is true, we need to construct a proof.
To show that a statement is false, we simply need to find a single counterexample where
it fails.
Adrian Dudek, Geoff Coates
Logic and Proof
26 / 33
Proof or Counterexample: Example
Consider the following statement:
Squaring a number makes it larger.
Adrian Dudek, Geoff Coates
Logic and Proof
27 / 33
Proof or Counterexample: Example
Consider the following statement:
Squaring a number makes it larger.
This statement is false. To disprove it, we simply need to demonstrate one instance
where it fails to be true.
Adrian Dudek, Geoff Coates
Logic and Proof
27 / 33
Proof or Counterexample: Example
Consider the following statement:
Squaring a number makes it larger.
This statement is false. To disprove it, we simply need to demonstrate one instance
where it fails to be true.
We can see that if we square the number 1, we get 1, which is not larger.
Adrian Dudek, Geoff Coates
Logic and Proof
27 / 33
Proof or Counterexample: Example
Consider the following statement:
Squaring a number makes it larger.
This statement is false. To disprove it, we simply need to demonstrate one instance
where it fails to be true.
We can see that if we square the number 1, we get 1, which is not larger.
So the above statement can not be true.
Adrian Dudek, Geoff Coates
Logic and Proof
27 / 33
Types of Proof: Contrapositives
There are many common types of proof. We have already seen deductive proofs using
algebra.
Adrian Dudek, Geoff Coates
Logic and Proof
28 / 33
Types of Proof: Contrapositives
There are many common types of proof. We have already seen deductive proofs using
algebra.
We know that a statement is true, if and only if its contrapositive is true. Sometimes it
turns out that it’s easier to prove the contrapositive of a statement rather than the
original statement itself. This is useful!
Adrian Dudek, Geoff Coates
Logic and Proof
28 / 33
Types of Proof: Proof by Contradiction
Proof by Contradiction works as follows.
Adrian Dudek, Geoff Coates
Logic and Proof
29 / 33
Types of Proof: Proof by Contradiction
Proof by Contradiction works as follows.
1
We are asked to prove that a statement is true.
Adrian Dudek, Geoff Coates
Logic and Proof
29 / 33
Types of Proof: Proof by Contradiction
Proof by Contradiction works as follows.
1
We are asked to prove that a statement is true.
2
We instead assume that the statement is false.
Adrian Dudek, Geoff Coates
Logic and Proof
29 / 33
Types of Proof: Proof by Contradiction
Proof by Contradiction works as follows.
1
We are asked to prove that a statement is true.
2
We instead assume that the statement is false.
3
We then show that this assumption leads to a contradiction.
Adrian Dudek, Geoff Coates
Logic and Proof
29 / 33
Types of Proof: Proof by Contradiction
Proof by Contradiction works as follows.
1
We are asked to prove that a statement is true.
2
We instead assume that the statement is false.
3
We then show that this assumption leads to a contradiction.
4
Reality forces the original statement to be true!
Adrian Dudek, Geoff Coates
Logic and Proof
29 / 33
Proof by Contradiction: Example
Use Proof by Contradiction to prove that
Adrian Dudek, Geoff Coates
Logic and Proof
√
2 is irrational. (Euclid 500BC)
30 / 33
Proof by Contradiction: Example
Use Proof by Contradiction to prove that
√
2 is irrational. (Euclid 500BC)
√
√
a
2 is rational, that is, 2 = where a and b are integers with no
b
common factors. (If they did have common factors we could cancel them out.)
Proof: Assume that
Adrian Dudek, Geoff Coates
Logic and Proof
30 / 33
Proof by Contradiction: Example
Use Proof by Contradiction to prove that
√
2 is irrational. (Euclid 500BC)
√
√
a
2 is rational, that is, 2 = where a and b are integers with no
b
common factors. (If they did have common factors we could cancel them out.)
Proof: Assume that
We want to show that this assumption yields a contradiction.
Adrian Dudek, Geoff Coates
Logic and Proof
30 / 33
Proof by Contradiction: Example
Use Proof by Contradiction to prove that
√
2 is irrational. (Euclid 500BC)
√
√
a
2 is rational, that is, 2 = where a and b are integers with no
b
common factors. (If they did have common factors we could cancel them out.)
Proof: Assume that
We want to show that this assumption yields a contradiction.
Squaring both sides of
2=
Adrian Dudek, Geoff Coates
√
a
2 = gives us:
b
a2
b2
Logic and Proof
30 / 33
Proof by Contradiction: Example
Use Proof by Contradiction to prove that
√
2 is irrational. (Euclid 500BC)
√
√
a
2 is rational, that is, 2 = where a and b are integers with no
b
common factors. (If they did have common factors we could cancel them out.)
Proof: Assume that
We want to show that this assumption yields a contradiction.
Squaring both sides of
2=
√
a
2 = gives us:
b
a2
b2
Rearranging this we get:
2b 2 = a2
Adrian Dudek, Geoff Coates
Logic and Proof
30 / 33
Proof by Contradiction: Example
2b 2 = a2
Adrian Dudek, Geoff Coates
Logic and Proof
31 / 33
Proof by Contradiction: Example
2b 2 = a2
We see that a2 must be even, because it is the product of 2 and some integer b 2 .
Adrian Dudek, Geoff Coates
Logic and Proof
31 / 33
Proof by Contradiction: Example
2b 2 = a2
We see that a2 must be even, because it is the product of 2 and some integer b 2 .
Now, we proved earlier (ie. added to our maths toolkit) that the product of two even
numbers is even. It’s not hard to show that the product of two odd numbers is odd
(exercise) so, if a2 is even, then a must also be even.
Adrian Dudek, Geoff Coates
Logic and Proof
31 / 33
Proof by Contradiction: Example
2b 2 = a2
We see that a2 must be even, because it is the product of 2 and some integer b 2 .
Now, we proved earlier (ie. added to our maths toolkit) that the product of two even
numbers is even. It’s not hard to show that the product of two odd numbers is odd
(exercise) so, if a2 is even, then a must also be even.
As a is even, we can write a = 2n for some integer n. Substituting this in we get:
2b 2 = (2n)2
Adrian Dudek, Geoff Coates
Logic and Proof
31 / 33
Proof by Contradiction: Example
2b 2 = a2
We see that a2 must be even, because it is the product of 2 and some integer b 2 .
Now, we proved earlier (ie. added to our maths toolkit) that the product of two even
numbers is even. It’s not hard to show that the product of two odd numbers is odd
(exercise) so, if a2 is even, then a must also be even.
As a is even, we can write a = 2n for some integer n. Substituting this in we get:
2b 2 = (2n)2
Expanding the bracket we get:
2b 2 = 4n2
Adrian Dudek, Geoff Coates
Logic and Proof
31 / 33
Proof by Contradiction: Example
2b 2 = a2
We see that a2 must be even, because it is the product of 2 and some integer b 2 .
Now, we proved earlier (ie. added to our maths toolkit) that the product of two even
numbers is even. It’s not hard to show that the product of two odd numbers is odd
(exercise) so, if a2 is even, then a must also be even.
As a is even, we can write a = 2n for some integer n. Substituting this in we get:
2b 2 = (2n)2
Expanding the bracket we get:
2b 2 = 4n2
Dividing by 2 we get:
b 2 = 2n2
Adrian Dudek, Geoff Coates
Logic and Proof
31 / 33
Proof by Contradiction: Example
b 2 = 2n2
Adrian Dudek, Geoff Coates
Logic and Proof
32 / 33
Proof by Contradiction: Example
b 2 = 2n2
Here we can see that b 2 must also be even, as it is the product of 2 and some other
integer n2 . So b must also be even.
Adrian Dudek, Geoff Coates
Logic and Proof
32 / 33
Proof by Contradiction: Example
b 2 = 2n2
Here we can see that b 2 must also be even, as it is the product of 2 and some other
integer n2 . So b must also be even.
We have established that both a and b are even. This means they both are divisible by 2.
Adrian Dudek, Geoff Coates
Logic and Proof
32 / 33
Proof by Contradiction: Example
b 2 = 2n2
Here we can see that b 2 must also be even, as it is the product of 2 and some other
integer n2 . So b must also be even.
We have established that both a and b are even. This means they both are divisible by 2.
However, we assumed that they had no factors in common. Thus, we have reached a
contradiction.
Adrian Dudek, Geoff Coates
Logic and Proof
32 / 33
Proof by Contradiction: Example
b 2 = 2n2
Here we can see that b 2 must also be even, as it is the product of 2 and some other
integer n2 . So b must also be even.
We have established that both a and b are even. This means they both are divisible by 2.
However, we assumed that they had no factors in common. Thus, we have reached a
contradiction.
∴
Adrian Dudek, Geoff Coates
√
2 is irrational. Logic and Proof
32 / 33
Using STUDYSmarter Resources
This resource was developed for UWA students by the STUDYSmarter team for the
numeracy program. When using our resources, please retain them in their original form
with both the STUDYSmarter heading and the UWA crest.
Adrian Dudek, Geoff Coates
Logic and Proof
33 / 33