* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download updated lecture notes 5
Neutron magnetic moment wikipedia , lookup
Magnetic field wikipedia , lookup
Magnetic monopole wikipedia , lookup
Electromagnetism wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Electrical resistance and conductance wikipedia , lookup
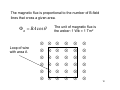
Superconductivity wikipedia , lookup
Lorentz force wikipedia , lookup
Chapter 20: Electromagnetic Induction •Motional EMF •Electric Generators •Faraday’s Law •Lenz’s Law •Transformers •Eddy Currents •Induced Electric Fields •Mutual- and Self-Inductance •LR Circuits 1 §20.1 Motional EMF Consider a conductor in a B-field moving to the right. ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ V ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ 2 FB = q(v × B ) An electron in the conductor experiences a force downward. eV The electrons in the bar will move toward the bottom of the bar. F This creates an electric field in the bar and results in a potential difference between the top and bottom of the bar. 3 What if the bar were placed across conducting rails (in red) so that there is a closed loop for the electrons to follow? ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ V ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ L In this circuit, the electrons flow clockwise; the current is counterclockwise. Öinduce emf because of motion 4 The motional EMF is ε = vBL where L is the separation between the rails. The current in the rod is ΔV ε vBL I= = = R R R where R is the resistance in the “wires”. 5 The rod has a current through it. What is the direction of the magnetic force on the rod due to the external magnetic field? F = I (L × B ) The magnitude of the magnetic force on the rod is: vBL vB 2 L2 LB = F = ILB sin 90° = ILB = R R Using the right hand rule, the force on the bar is directed to the left. 6 To maintain a constant EMF, the rod must be towed to the right with constant speed. An external agent must do work on the bar. (Energy conservation) 7 Faraday’s Law At the moment one closes the switch ammeter deflect and returns immediately to zero. Again deflection at the moment opening the switch There is no contact between the coils. We called this phenomenon a induce current. If we induce a current we have to have a potential difference: induced emf (electromotive force) 8 Other way to show: A coil experiences a current when magnetic passing through it varies 9 The magnetic flux is proportional to the number of B-field lines that cross a given area. Φ B = BA cos θ Loop of wire with area A The unit of magnetic flux is the weber: 1 Wb = 1 Tm2 ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ 10 Faraday’s Law: Φ final − Φ initial ΔΦ emf = − N = −N t final − tinitial Δt An induced EMF in a “coil” of N loops is due to a changing magnetic flux. Ways to induce an EMF: 1. Vary the magnetic field. 2. Vary the area of the coil. 3. Change the angle between B and A. 11 12 Example: If the magnetic field in a region varies with time according to the graph shown below, find the magnitude of the induced EMF in a single loop of wire during the following time intervals: (a) 0-2.0 ms, (b) 2.0-4.0 ms, and (c) 4.0-8.0 ms. The loop has area 0.500 m2 and the plane of the loop is perpendicular to the B-field. B (T) 0.50 T t (ms) 2 4 8 13 Example continued: Using Faraday’s Law: ⎛ ΔB ⎞ ⎛ ΔΦ B ⎞ ε = −⎜ ⎟ ⎟ = − A⎜ ⎝ Δt ⎠ ⎝ Δt ⎠ This is the slope of the given B versus time graph. 14 Example continued: (a) In the interval 0.0-2.0 ms, ⎛ ΔB ⎞ 2 ⎛ 0.50T-0.00T ⎞ ε = − A⎜ ⎟ = 130 V. ⎟ = 0.500 m ⎜ −3 ⎝ 2.0 × 10 s ⎠ ⎝ Δt ⎠ ( ) (b) In the interval 2.0-4.0 ms, ⎛ ΔB ⎞ 2 ⎛ 0.50T-0.50T ⎞ ε = − A⎜ ⎟ = 0 V. ⎟ = 0.500 m ⎜ −3 ⎝ 2.0 × 10 s ⎠ ⎝ Δt ⎠ ( ) 15 Example continued: (c) In the interval 4.0-8.0 ms, ⎛ ΔB ⎞ 2 ε = − A⎜ ⎟ = 0.500 m ⎝ Δt ⎠ ( ) ⎛ 0.00T-0.50T ⎞ ⎜ ⎟ = 63 V. −3 ⎝ 4.0 × 10 s ⎠ 16 Lenz’s Law The direction of induced EMFs and currents always oppose the change in flux that produced them. That is, the induced I (and thus induced B) tries to keep the total flux through the loop constant. 17 Example: Towing the bar to the right produced an induced current that was CCW. What is the direction of the induced magnetic field? ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ V ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ L The induced B is out of the page to maintain the flux originally through the loop before the bar started to move to the right (the area of the loop is increasing). 18 19 Example (text problem 20.12): A long straight wire carrying a steady current is in the plane of a circular loop of wire. (a) If the loop of wire is moved closer to the wire, what is the direction of the induced current in the wire loop? I Wire loop There is a magnetic field into the page at the location of the loop. As the loop gets closer to the wire there is an increase in flux. To negate this increase in flux, the induced B-field must point out of the page. This requires a CCW current. 20 Example continued: (b) At one instant, the induced EMF in the loop is 3.5 mV. What is the rate of change of the magnetic flux through the loop in that instant? ΔΦ B ε =− = 3.5 mV = 3.5 × 10 −3 Wb / s Δt 21 22 Electric Generators A coil of wire is spun in a magnetic field. This produces an EMF and also a current; both vary with time. (ACalternating current) An energy source is needed to turn the wire coil. Examples include burning coal or natural gas to produce steam; falling water. 23 The EMF produced by an AC generator is: ε (t ) = ε 0 sin ωt In the United States and Canada ε0 = 170 volts and f = ω/2π = 60 Hz. 24 §20.5 Transformers Wrap an iron core with wire. Primary coil Secondary coil Apply a varying voltage to the primary coil. This causes a changing magnetic flux in the secondary coil. ΔΦ B ε 1 = − N1 Δt ΔΦ B ε 2 = −N2 Δt 25 Since the flux through the coils is the same ε 1 N1 = ε 2 N2 The “turns ratio” gives the ratio of the EMFs. Depending on the turns ratio, a transformer can be used to step-up or step-down a voltage. The rate that power is supplied to both coils is the same ε 1 I 2 N1 = = ε 2 I1 N 2 26 Example (text problem 20.25): A step-down transformer has a turns ratio of 1/100. An AC voltage of amplitude 170 V is applied to the primary. If the primary current is 1.0 mA, what is the secondary current? I 2 N1 = I1 N 2 ⎛ N1 ⎞ ⎛ 100 ⎞ ⎟⎟ I1 = ⎜ I 2 = ⎜⎜ ⎟1.0 mA = 0.1 A ⎝ 1 ⎠ ⎝ N2 ⎠ 27 Example (text problem 20.27): The primary coil of a transformer has 250 turns and the secondary coil has 1000 turns. An AC voltage is sent through the primary. The EMF of the primary is 16.0 V. What is the EMF in the secondary? ε 1 N1 = ε 2 N2 ⎛ N2 ⎞ ⎛ 1000 ⎞ ε 2 = ⎜⎜ ⎟⎟ε 1 = ⎜ ⎟16.0 V = 64.0 V ⎝ 250 ⎠ ⎝ N1 ⎠ 28 Eddy Currents If a conductor is subjected to a changing magnetic flux, a current will flow. (This includes sheets of metal, etc.) 29 Consider a metal plate that swings through a magnetic field. pivot X An external magnetic field into the page created by a magnet. ⊗⊗⊗ ⊗⊗⊗ 30 As the plate swings through the region of magnetic field, some regions of the plate are entering the B-field (increasing flux), and other regions of the plate are leaving the B-field (decreasing flux). There will be induced currents in the conductor called eddy currents. The eddy currents dissipate energy (according to I2R); this results in the damping of the amplitude of the metal sheet. 31 Induced Electric Fields When a stationary conductor sits in a changing magnetic field it is an induced electric field that causes the charges in the conductor to move. 32 33 Mutual- and Self-Inductance A variable current I1 flows in coil 1. Coil 1 Coil 2 I1 then induces a current in coil 2. The flux (Φ21) through coil 2 due to coil 1 is N 2 Φ 21 ∝ I1. 34 Writing this as an equality, N 2 Φ 21 = MI1 Where M is the mutual inductance. It depends only on constants and geometrical factors. The unit of inductance is Henry (1H = 1Vs/A). ΔΦ 21 ΔI1 = −M ε 2 = −N2 Δt Δt The induced EMF in the coils will be: ΔΦ12 ΔI 2 ε 1 = − N1 = −M Δt Δt 35 Self-inductance occurs when a current carrying coil induces an EMF in itself. The definition of self-inductance (L) is NΦ = LI . 36 Example (text problem 20.41): The current in a 0.080 Henry solenoid increases from 20.0 mA to 160.0 mA in 7.0 s. Find the average EMF in the solenoid during that time interval. ΔΦ ΔI = −L ε = −N Δt Δt ⎛ 160 mA − 20 mA ⎞ = −(0.080 H )⎜ ⎟ 7.0 s ⎝ ⎠ = −1.6 × 10 −3 V 37 An inductor stores energy in its magnetic field according to: 1 2 U = LI 2 The energy density in a magnetic field is: uB = 1 2μ0 B2 38 §20.9 LR Circuits An inductor and resistor are connected in series to a battery. As with an RC circuit, the current in the circuit varies with time. 39 ΔI . The voltage drop across an inductor is given by ε L = L Δt When an inductor is “charging” (the energy stored is increasing) the current in the circuit is: ( I (t ) = I f 1 − e − t /τ ) Where τ = L/R is the time constant for the circuit and If = εb/R maximum current in the circuit. 40 Applying Kirchhoff’s loop rule to the circuit gives the EMF in the inductor as: ε L = ε b − IR = ε b e − t /τ 41 Plots of εL(t) and I(t) for this LR circuit: 42 For a “discharging” inductor, I (t ) = I 0 e − t /τ where I0 is the current in the inductor when t=0. The LR circuit time constant τ plays the same role as in an RC circuit. 43 Example: A coil has an inductance of 0.15 H and a resistance of 33.0 Ω. The coil is connected to a 6.0 V ideal battery. When the current reaches one-half the maximum value: (a) At what rate is the magnetic energy being stored in the inductor? ⎛ I max ⎞⎛ Vmax ⎞ Power = P = IV = ⎜ ⎟⎜ ⎟ ⎝ 2 ⎠⎝ 2 ⎠ Vmax= emf of the battery (εb) = 6.0 Volts I max = εb R = 0.18 Amps ⎛ I max ⎞⎛ Vmax ⎞ P=⎜ ⎟⎜ ⎟ = 0.27 Watts ⎝ 2 ⎠⎝ 2 ⎠ 44 Example continued: (b) At what rate is energy being dissipated? Energy is dissipated in the resistor at a rate 2 ⎛ I max ⎞ 2 P= I R=⎜ ⎟ R ⎝ 2 ⎠ 2 ⎛ 0.18 Amps ⎞ =⎜ ⎟ (33.0Ω ) = 0.27 Watts. 2 ⎝ ⎠ 45 Example continued: (c) What is the total power the battery supplies? The battery must supply energy to the inductor and the resistor. Part a and b calculate the rate at which energy is delivered to the inductor and resistor respectively; the battery must supply the sum of these: Pbattery = 0.54 Watts. 46 Summary •Motional EMF •Faraday’s Law •Lenz’s Law •Transformers •Eddy Currents •Inductance and Inductors •LR Circuits 47