Download Virtual geomagnetic poles

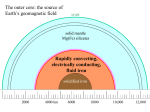
The outer core: the source of
Earth’s geomagnetic field
crust
solid mantle
Mg(Fe) silicates
Rapidly convecting,
electrically conducting,
fluid iron
solidified iron
2000
4000 km
6000
8000
10,000
12,000
crust
solid mantle
Mg(Fe) silicates
The geomagnetic dynamo:
• turbulent fluid convection
• electromagnetic interactions
in fluid, flowing conductor
• effects of rotation of earth
solidified iron
2000
4000 km
6000
8000
10,000
12,000
A snapshot of the 3D
magnetic field structure
simulated with the
Glatzmaier-Roberts
geodynamo model.
Magnetic field lines are
blue where the field is
directed inward and yellow
where directed outward.
The rotation axis of the
model Earth is vertical and
through the center. A
transition occurs at the
core-mantle boundary from
the intense, complicated
field structure in the fluid
core, where the field is
generated, to the smooth,
potential field structure
outside the core. The field
lines are drawn out to two
Earth radii. Magnetic field
is wrapped around the
"tangent cylinder" due to
the shear of the zonal fluid
flow.
90% of Earth’s geomagnetic field can
be represented by a simple dipole
located at the center of the earth!
Field of a bar magnet revealed
by iron filings
The dipole field has
axial symmetry
about the axis of
the dipole
The representation of the
geomagnetic field as an
earth-centered dipole
magnetic
north pole
magnetic field
vector
This is a planar
section through the
center of the earth,
which intersects the
surface as a “great
circle”
-p
h
two
twopoles
poleswith
withpole
polestrength
strength
-p
-pand
and+p
+prespectively,
respectively,separted
separted by
by
a distance
h form
dipole;
a distance
h form
thethe
magnetic
its
strength
measured
by the by
dipole;
its is
strength
is measured
product
of pof
andp h,
termed
the the
the product
and
h, termed
dipole
dipolemoment.
moment.The
Themagnetic
magnetic
poles
polesare
areseparated
separatedalong
alongaaline,
line,
the
thedipole
dipoleaxis,
axis,which
whichintersects
intersects
the
thesurface
surfaceatatthe
themagnetic
magneticnorth
north
and
south
poles.
and south poles.
axis of dipole
+p
magnetic equator
magnetic
south pole
magnetic
north pole
Field from dipole = vector
composition of the fields from
the two poles
-p
h
+p
R
magnetic
north pole
Field from dipole = vector
composition of the fields from
the two poles
-p
h
R
+p
magnetic
north pole
Field from dipole = vector
composition of the fields from
the two poles
R
-p
h
+p
magnetic
north pole
Field from dipole = vector
composition of the fields from
the two poles
-p
h
R
+p
magnetic
north pole
Field from dipole = vector
composition of the fields from
the two poles
Note the symmetry:
1. this section is the same for
any great circle section
that includes the dipole
axis;
2. The magnetic field is
always in such a section;
3. The horizontal component
of the field is always along
a great circle passing
through the magnetic north
pole.
-p
h
+p
R
q = geomagnetic co-latitude
Inclination = I
geomagnetic field
vector measured at
observation site
-p
+p
magnetic equator
Relationship between inclination, I and
geomagnetic co-latitude, q :
axis of dipole
This great circle
passes through the
observation site
and the magnetic
north and south
poles
geomagnetic
north pole
magnetic
south pole
tan(I) = 2/tan(q)
This is a key relationship in paleomagnetism:
from measurement of I in a magnetized rock
sample one can calculate the angular distance to
the geomagnetic pole (the “virtual geomagnetic
pole” or VGP).
geomagnetic field components: F, I and D
F = H  magnitude of
the geomagnetic field vector
F = "total intensity"
down
H  geomagnetic field vector
geomagnetic field components: F, I and D
I
I = inclination, angle
measured from surface in
vertical plane to the
geomagnetic field vector
vertical
component
down
H  geomagnetic field vector
geomagnetic field components: F, I and D
D
D = declination, angle
measured in horizontal
plane clockwise from
North
vertical
component
down
H  geomagnetic field vector
D as the angle between two great circles that intersect
at the site location
Great circle line of
longitude between site
location and north pole
D
Horizontal component
Points in the direction of
magnetic North, along the
great circle joining the site
and the geomagnetic pole
vertical
component
down
H  geomagnetic field vector
North Pole (NP)
Measurement of D and I at a site
location determines the location of
the north geomagnetic pole if it is
assumed that the field is entirely a
simple earth centered dipole field.
This determines the location of the
“Virtual Geomagnetic Pole” or
VGP
site where
magnetic field is
measured
North Pole (NP)
This is the
longitudinal great
circle that passes
through the North
Pole and the
observation site
site where
magnetic field is
measured
VGP
North Pole (NP)
VGP
site where
magnetic field is
measured
This is the great circle
through the observation site
and the VGP; it is the same
great circle shown in sections
in the preceding figures.
This is the
longitudinal
great circle
that passes
through the
observation
site
Red grid: geomagnetic
latitudes and longitudes
about geomagnetic pole
(shown as VGP here)
This is the great
circle through the
observation site
and the VGP; it is
the same great
circle shown in
section in the
preceding figures.
Black grid: geographic
latitudes and longitudes
Declination
Locations of the
north pole of the
dipole component of
the geomagnetic
field from 19452000.
Magnetization of rocks
Detrital Remanent Magnetization (DRM)
•formed during deposition of sediments
• locked in by compaction and lithification to
sedimentary rock
• relatively weak, but persistent over geological time
scales
Magnetization of rocks
Thermo-remanent Magnetization (TRM)
• formed in basic igneous rocks (e.g., basalt) upon
cooling through Curie temperature
• locked in for geological time scales upon further
cooling
• very strong and persistent
Magnetization of rocks
Thermo-remanent Magnetization (TRM)
Magnetization of rocks
In both types of magnetization, the time of acquisiton of
the stable magnitization must be
 short
 determinable (mainly via isotope geochemistry)
positions of the north magnetic pole during the past 3700 years.
-30 to 3690 BP
Average pole position
for all data
(94 poles):
88.4 N
23.8 W
1.6 degrees from
geographic North Pole
-30 to 800 BP
800 to 1940 BP
1940 to 3690 BP
Calibrated radiocarbon years before
present, (B.P, AD1950=0)
90 E
VGP’s average Earth’s
rotation axis!
Polar projection showing VGP’s
for igneous rocks at many sites, all
dated at less than 20 million years
old (too young to be significantly
affected by plate motions).
North Pole
180
0
90 W
Why Virtual Geomagnetic Pole?
90% of the modern geomagnetic field is represented by a
simple dipole at the center of the earth. The remaining 10%,
the “non-dipole” components, have a more complicated
spatial structure. Geomagneticians assume that in the past
the earth’s field was also dominated by the dipole
component. We can derive the location of the geomagnetic
pole from an observation of inclination and declination at a
site as indicated in the previous slides, by assuming that only
the simple dipole is present, i.e., ignoring the non-dipole
components. This produces an estimate of the location of the
dipole component that we call the “virtual geomagnetic
pole”. If we determine many VGP’s from many different
locations and average the results, we obtain an estimate of
the orientation of the dipole component of the field. This is
the basic assumption for paleomagnetic determinations of
past locations of areas relative to Earth’s rotation axis.
Lab questions
1. The southeastern coastal area of Alaska has a geology very different than areas farther inland,
suggesting very different history – suggesting that the coastal area was a terrane that had accreted
onto Alaska in Late Cretaceous (100 Ma). Reliable paleomagnetic measurements taken on Early
Jurassic (200 Ma) samples in the accreted terrane and in the interior are listed below. The two
sampled areas are close enough to one another that you can assume that they are essentially at the
same location.
Accreted terrane: Declination = N10°W (= -10°), Inclination = +63° (magnetic field pointing
downwards).
Interior area: Declination = N10°E (= +10°), Inclination = +85°
a. Calculate the latitudes of each area in the Early Jurassic.
b. Estimate the minimum velocity of the accreted terrane relative to the interior site between 200
and 100 Ma. (in units of centimeters/year). Explain why this is a minimum estimate. Assume an
earth radius of 6371 km.
2. Specify the location of the VGP's (location of virtual north magnetic pole) for the following cases:
a. site latitude = 20.0 S; site longitude = 65.0 W; declination = 0.0; inclination = 0.0
b. site latitude = 20.0 S; site longitude = 30.0 E; declination = 0.0; inclination = 0.0
c. site latitude = 0.0 (equator); site longitude = 30.0 E; declination = 050 (N 50 E); inclination = 0.0
d. site latitude = 0.0 (equator); site longitude = 30.0 E; declination = 050 (N 50 E); inclination = -90
(magnetic vector pointing vertically upwards)