* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Equivalence relations and Counting
A New Kind of Science wikipedia , lookup
Ethnomathematics wikipedia , lookup
Positional notation wikipedia , lookup
Hyperreal number wikipedia , lookup
Virtual work wikipedia , lookup
Proofs of Fermat's little theorem wikipedia , lookup
Abuse of notation wikipedia , lookup
Principia Mathematica wikipedia , lookup
Equivalence Relations
Counting
CITS2211 Discrete Structures (2016)
Equivalence relations and Counting
Pigeonhole Principle
Equivalence Relations
Counting
Pigeonhole Principle
Equivalence relations
Definition
An equivalence relation is a relation on a set A that is reflexive,
transitive and symmetric.
We shall see that equivalence relations “group together” elements
from the domain.
Equivalence Relations
Counting
Pigeonhole Principle
Example
Let A = {0, 1, 2, . . . , 8} and define a relation R by (a, b) ∈ R if
and only if b − a is a multiple of 3.
In more formal language we would write
R = {(a, b) : 3 | b − a}
where the vertical bar “|” means “is a divisor of”.
For example (2, 5) ∈ R and (5, 8) ∈ R but (2, 4) ∈
/ R and
(3, 4) ∈
/ R.
Equivalence Relations
Counting
Pigeonhole Principle
Example cont.
Because this is a finite example, we can just list all of the elements
of A × A, and decide which belong to R.
(0, 0)
(1, 0)
(2, 0)
(3, 0)
(4, 0)
(5, 0)
(6, 0)
(7, 0)
(8, 0)
(0, 1)
(1, 1)
(2, 1)
(3, 1)
(4, 1)
(5, 1)
(6, 1)
(7, 1)
(8, 1)
(0, 2)
(1, 2)
(2, 2)
(3, 2)
(4, 2)
(5, 2)
(6, 2)
(7, 2)
(8, 2)
(0, 3)
(1, 3)
(2, 3)
(3, 3)
(4, 3)
(5, 3)
(6, 3)
(7, 3)
(8, 3)
(0, 4)
(1, 4)
(2, 4)
(3, 4)
(4, 4)
(5, 4)
(6, 4)
(7, 4)
(8, 4)
(0, 5)
(1, 5)
(2, 5)
(3, 5)
(4, 5)
(5, 5)
(6, 5)
(7, 5)
(8, 5)
(0, 6)
(1, 6)
(2, 6)
(3, 6)
(4, 6)
(5, 6)
(6, 6)
(7, 6)
(8, 6)
(0, 7)
(1, 7)
(2, 7)
(3, 7)
(4, 7)
(5, 7)
(6, 7)
(7, 7)
(8, 7)
(0, 8)
(1, 8)
(2, 8)
(3, 8)
(4, 8)
(5, 8)
(6, 8)
(7, 8)
(8, 8)
Equivalence Relations
Counting
Pigeonhole Principle
Example cont.
Because this is a finite example, we can just list all of the elements
of A × A, and decide which belong to R.
(0, 0)
(1, 0)
(2, 0)
(3, 0)
(4, 0)
(5, 0)
(6, 0)
(7, 0)
(8, 0)
(0, 1)
(1, 1)
(2, 1)
(3, 1)
(4, 1)
(5, 1)
(6, 1)
(7, 1)
(8, 1)
(0, 2)
(1, 2)
(2, 2)
(3, 2)
(4, 2)
(5, 2)
(6, 2)
(7, 2)
(8, 2)
(0, 3)
(1, 3)
(2, 3)
(3, 3)
(4, 3)
(5, 3)
(6, 3)
(7, 3)
(8, 3)
(0, 4)
(1, 4)
(2, 4)
(3, 4)
(4, 4)
(5, 4)
(6, 4)
(7, 4)
(8, 4)
(0, 5)
(1, 5)
(2, 5)
(3, 5)
(4, 5)
(5, 5)
(6, 5)
(7, 5)
(8, 5)
(0, 6)
(1, 6)
(2, 6)
(3, 6)
(4, 6)
(5, 6)
(6, 6)
(7, 6)
(8, 6)
(0, 7)
(1, 7)
(2, 7)
(3, 7)
(4, 7)
(5, 7)
(6, 7)
(7, 7)
(8, 7)
(0, 8)
(1, 8)
(2, 8)
(3, 8)
(4, 8)
(5, 8)
(6, 8)
(7, 8)
(8, 8)
Equivalence Relations
Counting
Pigeonhole Principle
Example: reflexive
As 3 divides 0, we have all the pairs of the form (a, a), and so the
relation is reflexive.
(0, 0)
(1, 0)
(2, 0)
(3, 0)
(4, 0)
(5, 0)
(6, 0)
(7, 0)
(8, 0)
(0, 1)
(1, 1)
(2, 1)
(3, 1)
(4, 1)
(5, 1)
(6, 1)
(7, 1)
(8, 1)
(0, 2)
(1, 2)
(2, 2)
(3, 2)
(4, 2)
(5, 2)
(6, 2)
(7, 2)
(8, 2)
(0, 3)
(1, 3)
(2, 3)
(3, 3)
(4, 3)
(5, 3)
(6, 3)
(7, 3)
(8, 3)
(0, 4)
(1, 4)
(2, 4)
(3, 4)
(4, 4)
(5, 4)
(6, 4)
(7, 4)
(8, 4)
(0, 5)
(1, 5)
(2, 5)
(3, 5)
(4, 5)
(5, 5)
(6, 5)
(7, 5)
(8, 5)
(0, 6)
(1, 6)
(2, 6)
(3, 6)
(4, 6)
(5, 6)
(6, 6)
(7, 6)
(8, 6)
(0, 7)
(1, 7)
(2, 7)
(3, 7)
(4, 7)
(5, 7)
(6, 7)
(7, 7)
(8, 7)
(0, 8)
(1, 8)
(2, 8)
(3, 8)
(4, 8)
(5, 8)
(6, 8)
(7, 8)
(8, 8)
Equivalence Relations
Counting
Pigeonhole Principle
Example: symmetric
Whenever we have 3 | b − a, then also 3 | a − b and so the relation
is symmetric.
(0, 0)
(1, 0)
(2, 0)
(3, 0)
(4, 0)
(5, 0)
(6, 0)
(7, 0)
(8, 0)
(0, 1)
(1, 1)
(2, 1)
(3, 1)
(4, 1)
(5, 1)
(6, 1)
(7, 1)
(8, 1)
(0, 2)
(1, 2)
(2, 2)
(3, 2)
(4, 2)
(5, 2)
(6, 2)
(7, 2)
(8, 2)
(0, 3)
(1, 3)
(2, 3)
(3, 3)
(4, 3)
(5, 3)
(6, 3)
(7, 3)
(8, 3)
(0, 4)
(1, 4)
(2, 4)
(3, 4)
(4, 4)
(5, 4)
(6, 4)
(7, 4)
(8, 4)
(0, 5)
(1, 5)
(2, 5)
(3, 5)
(4, 5)
(5, 5)
(6, 5)
(7, 5)
(8, 5)
(0, 6)
(1, 6)
(2, 6)
(3, 6)
(4, 6)
(5, 6)
(6, 6)
(7, 6)
(8, 6)
(0, 7)
(1, 7)
(2, 7)
(3, 7)
(4, 7)
(5, 7)
(6, 7)
(7, 7)
(8, 7)
(0, 8)
(1, 8)
(2, 8)
(3, 8)
(4, 8)
(5, 8)
(6, 8)
(7, 8)
(8, 8)
Equivalence Relations
Counting
Pigeonhole Principle
The directed graph
The directed graph of the relation:
3
4
0
6
5
1
7
2
8
Notice it is a disjoint union of cliques.
We can easily check from the graph that R is transitive.
Equivalence Relations
Counting
Pigeonhole Principle
Another relation
Let’s be more ambitious this time, and consider an infinite relation
R on the integers Z, defined by
R = {(a, b) : 3 | b − a}
As we can’t list all the pairs in the relation, we have to argue
symbolically to prove that the three properties hold.
Reflexivity
For any a ∈ Z it is true that 3 | a − a and so (a, a) ∈ R.
Symmetry
If (a, b) ∈ R then b − a = 3k for some k ∈ Z. But then
a − b = 3(−k) and as −k ∈ Z we have (b, a) ∈ R.
Equivalence Relations
Counting
Pigeonhole Principle
Transitivity
Proving transitivity usually needs the longest proof.
Transitivity
Suppose that (a, b), (b, c) ∈ R. Then ∃k1 , k2 ∈ Z such that
b = a + 3k1
c = b + 3k2
From this we see that
c = (a + 3k1 ) + 3k2
= a + 3(k1 + k2 )
= a + 3k
where k ∈ Z, and therefore (a, c) ∈ R.
Equivalence Relations
Counting
Pigeonhole Principle
The directed graph
This is a bit harder to draw because now it is an infinite graph, but
let’s draw a bit of it, starting with vertex 0.
0
3
−3
−6
6
−9
9
Infinitely more numbers omitted
It is easy to see that (0, 3) ∈ R, (0, 6) ∈ R, (0, 9) ∈ R and so on,
and as the relation is symmetric we use a line without arrows to
indicate a 2-way connection.
Equivalence Relations
Counting
Pigeonhole Principle
But the relation is transitive
0
3
−3
−6
6
−9
9
Infinitely more numbers omitted
Equivalence Relations
Counting
Pigeonhole Principle
But the relation is transitive
0
3
−3
−6
6
−9
9
Infinitely more numbers omitted
Equivalence Relations
Counting
Pigeonhole Principle
But the relation is transitive
0
3
−3
−6
6
−9
9
Infinitely more numbers omitted
Equivalence Relations
Counting
Pigeonhole Principle
But the relation is transitive
0
3
−3
−6
6
−9
9
Infinitely more numbers omitted
So again we discover a clique — a set of elements with every
possible connection between them
Equivalence Relations
Counting
Pigeonhole Principle
Another clique
So the set of numbers
{. . . , −9, −6, −3, 0, 3, 6, 9 . . .}
form a clique. Similarly
{. . . , −8, −5, −2, 1, 4, 7, 10 . . .}
and
{. . . , −7, −4, −1, 2, 5, 8, 11 . . .}
forms a third clique.
So the graph of this relation consists of three cliques; inside each
clique every possible connection is present, while between the
cliques there are no connections at all.
Equivalence Relations
Counting
Pigeonhole Principle
The final graph
0
3
6
9
−3
−6
−9
1
4
7
10
2
−2
5
−5
−8
8
11
−1
−4
−7
Equivalence Relations
Counting
Pigeonhole Principle
The general situation
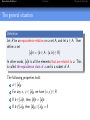
Definition
Let R be an equivalence relation on a set A, and let a ∈ A. Then
define a set
[a]R = {b ∈ A : (a, b) ∈ R}
In other words, [a]R is all the elements that are related to a. This
is called the equivalence class of a and is a subset of A.
The following properties hold:
1
a ∈ [a]R
2
For any x, y ∈ [a]R we have (x, y ) ∈ R
3
If b ∈ [a]R , then [b]R = [a]R .
4
If b ∈
/ [a]R then [b]R ∩ [a]R = ∅
Equivalence Relations
Counting
Pigeonhole Principle
Property 1
Need to Show: a ∈ [a]R
An equivalence relation is reflexive and so for any a ∈ A, we have
(a, a) ∈ R.
Therefore a ∈ [a]R .
Equivalence Relations
Counting
Pigeonhole Principle
Property 2
Need to Show: For any x, y ∈ [a]R we have (x, y ) ∈ R
− Let x, y be two elements of [a]R
− As x, y ∈ [a]R we know that (a, x) ∈ R and (a, y ) ∈ R
− As R is symmetric and (a, x) ∈ R, it follows that (x, a) ∈ R.
− As R is transitive and (x, a) ∈ R, (a, y ) ∈ R it follows that
(x, y ) ∈ R.
Therefore for any x, y ∈ [a]R we have (x, y ) ∈ R
Equivalence Relations
Counting
Pigeonhole Principle
Property 3
Need to Show: If b ∈ [a]R , then [b]R = [a]R .
− If x ∈ [b]R then (b, x) ∈ R
− As b ∈ [a]R it follows that (a, b) ∈ R
− As (a, b), (b, x) ∈ R, it follows (transitivity) that x ∈ [a]R
Therefore [b]R ⊆ [a]R .
If b ∈ [a]R then a ∈ [b]R and so the same argument with a, b
exchanged shows that [a]R ⊆ [b]R , and hence the two sets are
equal.
Equivalence Relations
Counting
Pigeonhole Principle
Property 4
Need to Show: If b ∈
/ [a]R , then [b]R ∩ [a]R = ∅.
− If x ∈ [b]R ∩ [a]R then (a, x) ∈ R and (b, x) ∈ R
− As R is symmetric and (b, x) ∈ R, it follows that (x, b) ∈ R
− As R is transitive and (a, x), (x, b) ∈ R, it follows that
(a, b) ∈ R.
We have therefore shown that if [a]R and [b]R have any elements
in common, then b ∈ [a]R . Therefore if b 6∈ [a]R it must be the
case that [a]R and [b]R are disjoint
Equivalence Relations
Counting
Pigeonhole Principle
The dénoument
Let R be an equivalence relation on a set A.
a
The equivalence classes form a partition of the underlying set.
Equivalence Relations
Counting
Pigeonhole Principle
The dénoument
Let R be an equivalence relation on a set A.
a
[a]R
The equivalence classes form a partition of the underlying set.
Equivalence Relations
Counting
Pigeonhole Principle
The dénoument
Let R be an equivalence relation on a set A.
a
b
[a]R
The equivalence classes form a partition of the underlying set.
Equivalence Relations
Counting
Pigeonhole Principle
The dénoument
Let R be an equivalence relation on a set A.
a
b
[a]R
[b]R
The equivalence classes form a partition of the underlying set.
Equivalence Relations
Counting
Pigeonhole Principle
The dénoument
Let R be an equivalence relation on a set A.
a
b
c
[a]R
[b]R
[c]R
The equivalence classes form a partition of the underlying set.
Equivalence Relations
Counting
Pigeonhole Principle
The dénoument
Let R be an equivalence relation on a set A.
a
b
c
[a]R
[b]R
[c]R
...
The equivalence classes form a partition of the underlying set.
Equivalence Relations
Counting
Pigeonhole Principle
Partitions
Definition
A partition of a set A is a collection of subsets A1 , A2 , A3 , . . .,
such that
A = A1 ∪ A2 ∪ · · ·
and for any i 6= j,
Ai ∩ Aj = ∅.
So the equivalence classes of an equivalence relation form a
partition of the underlying set.
Equivalence Relations
Counting
Another example
Define a relation on the integers Z by the following rule
R = {(x, y ) : |x| = |y |}
where |x| is the absolute value of x.
So for example,
(1, 1) ∈ R,
(1, −1) ∈ R
but
(1, 2) ∈
/ R.
Pigeonhole Principle
Equivalence Relations
Counting
Pigeonhole Principle
Prove the properties
Reflexive
As |x| = |x| for all x ∈ Z, it follows that (x, x) ∈ R.
Symmetric
If (x, y ) ∈ R then |x| = |y |, so clearly |y | = |x| and therefore
(y , x) ∈ R.
Transitive
If (x, y ), (y , z) ∈ R then |x| = |y | and |y | = |z| so clearly
|x| = |z| and therefore (x, z) ∈ R.
Equivalence Relations
Counting
Pigeonhole Principle
What are the equivalence classes?
We start by finding [0]R – the equivalence class containing 0 – so
need to find all the integers x such that (0, x) ∈ R, in other words
all the integers satisfying |0| = |x|.
A moment’s thought tells us that x = 0 is the only integer with
absolute value 0, and so
[0]R = {0}
Equivalence Relations
Counting
Pigeonhole Principle
What are the equivalence classes?
We start by finding [0]R – the equivalence class containing 0 – so
need to find all the integers x such that (0, x) ∈ R, in other words
all the integers satisfying |0| = |x|.
A moment’s thought tells us that x = 0 is the only integer with
absolute value 0, and so
[0]R = {0}
Now find the equivalence class containing 1 – what integers x have
the property that (1, x) ∈ R?
Equivalence Relations
Counting
Pigeonhole Principle
What are the equivalence classes?
We start by finding [0]R – the equivalence class containing 0 – so
need to find all the integers x such that (0, x) ∈ R, in other words
all the integers satisfying |0| = |x|.
A moment’s thought tells us that x = 0 is the only integer with
absolute value 0, and so
[0]R = {0}
Now find the equivalence class containing 1 – what integers x have
the property that (1, x) ∈ R?
[1]R = {−1, 1}
Equivalence Relations
Counting
Pigeonhole Principle
And so on
It is then easy to see that the equivalence classes are given by
[0]R = {0}
[1]R = {−1, 1}
[2]R = {−2, 2}
..
.
[n]R = {−n, n}
..
.
Equivalence Relations
Counting
Pigeonhole Principle
Start with a partition
Let X = {0, 1, 2, 3, 4, 5} and consider the following partition of X
P = {0, 1, 2 | 3, 4 | 5}
into three parts X1 = {0, 1, 2}, X2 = {3, 4} and X3 = {5}.
Now, define a relation R on the set X by (x, y ) ∈ R if x and y lie
in the same cell of P. So
R = {(0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (1, 2), (2, 0),(2, 1), (2, 2),
(3, 3), (3, 4), (4, 3), (4, 4), (5, 5)}
Equivalence Relations
Counting
Pigeonhole Principle
Is this an equivalence relation
We can easily check by hand that this is an equivalence relation.
The equivalence classes are
[0]R = {0, 1, 2}
[3]R = {3, 4}
[5]R = {5}
Thus the partition into equivalence classes is the same as the
original partition used to define the relation.
Equivalence Relations
Counting
Pigeonhole Principle
Conclusion
We’ve seen the following two facts
1
An equivalence relation on a set A gives rise to a partition of A
2
A partition of A gives rise to an equivalence relation on A
Therefore equivalence relations and partitions are really “the same
thing” — or more precisely they are different ways of looking at
the same thing.
Equivalence Relations
Counting
Pigeonhole Principle
Counting principles
Counting is a fundamental activity for both mathematicians and
computer scientists.
Determining how much time and/or space a program might use
often requires counting (e.g. the size of the search space)
We’ll cover
The inclusion-exclusion formula
The multiplication principle of counting
The pigeonhole principle
Equivalence Relations
Counting
Pigeonhole Principle
The inclusion-exclusion formula
Inclusion-exclusion formula
The inclusion-exclusion formula is derived from the cardinality of
the union of two sets:
| A ∪ B |=| A | + | B | − | A ∩ B |
The size of set A ∪ B is sum of the sizes of A and B minus the
number of elements in A ∩ B which would otherwise be counted
twice.
Recall that the number of elements in a set A is denoted | A | (or
sometimes just size(A)).
Equivalence Relations
Counting
Pigeonhole Principle
Example
In a group of 90 students studying Discrete Structures, 70 can
program in Java and 50 can program in Python. 40 can program
in both Java and Python.
How many of the students can not program in either of these
languages ?
Equivalence Relations
Counting
Pigeonhole Principle
Let J be set of Java programmers with | J |= 70.
Let P be the set of Python programmers with | P |= 50.
The number of programmers of both languages is | J ∩ P |= 40.
The number of students with at least one language is:
| J ∪ P |=| J | + | P | − | J ∩ P |= 70 + 50 − 40 = 80
We need to find | J ∪ P | (the set complement).
90 students study Discrete structures. 80 know Java or Python.
So there are 10 students who can not program in either Java or
Python.
Equivalence Relations
Counting
Pigeonhole Principle
The multiplication principle
Multiplication Principle
If there are nA possible outcomes for an event A and nB possible
outcomes for an event B (that is independent of event A), then
there are
nA × nB
possible outcomes for the sequence of events A followed by B.
Equivalence Relations
Counting
Example
An ice-cream shop offers
Cups, Plain cone, Sugar cone, Waffle cone
Chocolate, Strawberry or Vanilla
How many choices are there for a single scoop?
Pigeonhole Principle
Equivalence Relations
Counting
Pigeonhole Principle
Example
An ice-cream shop offers
Cups, Plain cone, Sugar cone, Waffle cone
Chocolate, Strawberry or Vanilla
How many choices are there for a single scoop?
Here A is the event “choose a cup/cone” with nA = 4 outcomes,
while B is the event “choose a flavour” with nB = 3 outcomes,
and so there are 12 total outcomes.
Equivalence Relations
Counting
Pigeonhole Principle
Cartesian Product
Recall A × B = {(a, b) : a ∈ A, b ∈ B}.
What is the cardinality of A × B if |A| = m and |B| = n?
We need to choose a from A and choose b from B.
first event: to choose the first coordinate → m possible
outcomes.
second event: to choose the second coordinate → n possible
outcomes.
These events are independent, so by the multiplication principle,
|A × B| = mn = |A| × |B|.
Equivalence Relations
Counting
Pigeonhole Principle
The extended multiplication principle
If there are k events, A1 , A2 , . . ., Ak that have n1 , n2 , . . ., nk
outcomes respectively, all independent of each other.
Then there are
n1 × n2 × · · · × nk
possible outcomes for the sequence of events A1 , A2 , . . . Ak .
Equivalence Relations
Counting
Pigeonhole Principle
Extended multiplication principle: example
How many passwords are there that consist of four lower-case
characters, followed by two digits?
Equivalence Relations
Counting
Pigeonhole Principle
Extended multiplication principle: example
How many passwords are there that consist of four lower-case
characters, followed by two digits?
There are 26 choices for the first character, 26 for the second, 26
for the third, 26 for the fourth and then 10 choices for the fifth
and sixth, so the total number of choices is
26 × 26 × 26 × 26 × 10 × 10
Equivalence Relations
Counting
Pigeonhole Principle
Counting functions
How many functions f : {0, 1} → {a, b, c, d} are there?
d
0
c
1
b
a
Let A be the event “choose a value for f (0)” which has 4 possible
outcomes (shown in red),
Equivalence Relations
Counting
Pigeonhole Principle
Counting functions
How many functions f : {0, 1} → {a, b, c, d} are there?
d
0
c
1
b
a
Let A be the event “choose a value for f (0)” which has 4 possible
outcomes (shown in red),
Let B be the event “choose a value for f (1)” which has 4 possible
outcomes (shown in blue).
Since these two events are independent, by the multiplication
principle, there are 42 = 16 such functions.
Equivalence Relations
Counting
Pigeonhole Principle
Counting functions
More generally, if |A| = m and |B| = n, then how many functions
with domain A and codomain B are there?
Equivalence Relations
Counting
Pigeonhole Principle
Counting functions
More generally, if |A| = m and |B| = n, then how many functions
with domain A and codomain B are there?
Answer: We have n possible outcomes for the value of f (a), and m
values a to consider, so the number is
m
|A|
n
| ×n×
{z. . . × n} = n = |B| ,
m times
by the extended multiplication principle.
Equivalence Relations
Counting
Pigeonhole Principle
Binary strings
How many binary strings are there of length n?
Let A1 be the event “select a value for the first character”, so
n1 = 2, let A2 be the event “select a value for the second
character” with n2 = 2, and so on.
Thus the total number is
n
|2 × 2 ×
{z. . . × 2} = 2
n times
0000
0100
1000
1100
0001
0101
1001
1101
0010
0110
1010
1110
0011
0111
1011
1111
When n = 4, we have 16 choices.
Equivalence Relations
Counting
Pigeonhole Principle
Subsets of a set
Let A = {a1 , a2 , . . . , ak } be a set. How many subsets does A have?
Here we notice that there are the same number of subsets of A as
there are binary strings of length k.
a1
0
a2
1
a3
0
a4
0
a5
1
...
...
ak
1
Equivalence Relations
Counting
Pigeonhole Principle
Subsets of a set
Let A = {a1 , a2 , . . . , ak } be a set. How many subsets does A have?
Here we notice that there are the same number of subsets of A as
there are binary strings of length k.
a1
0
a1
a2
1
a2
a3
0
a3
a4
0
a4
a5
1
a5
...
...
...
ak
1
ak
yields
{a2 , a5 , . . . , ak }
So the answer is 2k .
|P(A)| = 2|A| , when A is a finite set.
Exercise: Define formally a bijection between the set of binary
strings of length k and P(A) (and prove it is a bijection).
Equivalence Relations
Counting
Pigeonhole Principle
Counting relations
Let’s count relations. Recall a relation is a subset of the Cartesian
product of A and B.
Suppose that |A| = m, and |B| = n, and consider the number of
relations with domain A and codomain B.
We know A × B has cardinality mn, and by the previous slide, the
number of subsets of A × B is 2mn .
1
b
1
b
1
b
1
b
1
b
1
b
1
b
1
b
0
a
0
a
0
a
0
a
0
a
0
a
0
a
0
a
1
b
1
b
1
b
1
b
1
b
1
b
1
b
1
b
0
a
0
a
0
a
0
a
0
a
0
a
0
a
0
a
Equivalence Relations
Counting
Pigeonhole Principle
Complications
Complications usually arise from events not being independent or
additional constraints, but often the principle can be modified.
For example,
How many passwords are there consisting of six lower-case
characters, with no consecutive characters equal?
How many passwords are there consisting of five lower-case
characters and a single digit (in any order)?
Equivalence Relations
Counting
Pigeonhole Principle
Not independent
When counting passwords with six lower-case characters, with no
consecutive characters equal there are still 26 choices for the first
character, but now the choice of second character depends on the
first choice.
In this case, it is easy to see that the number of remaining choices
for the second character is 25, and similarly for the rest of the
characters, so the answer is
26 × 25 × 25 × 25 × 25 × 25 = 26 × 255
More complicated rules will lead to much more complicated
counting problems.
Equivalence Relations
Counting
Pigeonhole Principle
Additional constraints
The number of passwords with five lower-case characters and a
single digit is harder to calculate — although there are 26 + 10
choices for the first character, we cannot determine the number of
choices for the second, because it depends totally on which choice
was made for the first character.
Equivalence Relations
Counting
Pigeonhole Principle
Additional constraints
The number of passwords with five lower-case characters and a
single digit is harder to calculate — although there are 26 + 10
choices for the first character, we cannot determine the number of
choices for the second, because it depends totally on which choice
was made for the first character.
The best way to proceed here is to split the problem into a number
of smaller problems that we can solve; in other words find the
number of passwords of each of the following forms:
dααααα
αdαααα
ααdααα
αααdαα
ααααdα
αααααd
where d means “a digit” and α means “a letter”.
Equivalence Relations
Counting
Pigeonhole Principle
Challenge problem
How many passwords are there that meet the following
requirements?
The length is exactly six characters
It must contain at least one digit and at most two digits
The non-digit characters are lower case letters
Equivalence Relations
Counting
Pigeonhole Principle
The pigeonhole principle
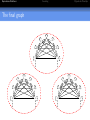
If 10 pigeons have 9 pigeonholes, then at least one pigeonhole
contains two pigeons.
Equivalence Relations
Counting
Pigeonhole Principle
More generally
Pigeonhole Principle If n items are assigned to m < n groups, then
at least two items are assigned to the same group.
If 13 people are at a dinner, then at least two of them have
the same birth month.
If 51 integers are chosen from the set {1, 2, . . . , 100}, then at
least two are consecutive.
If 10 integers are chosen randomly from the set
{1, 2, . . . , 100} then the resulting set has at least two disjoint
subsets with the same sum.
Equivalence Relations
Counting
Pigeonhole Principle
Proofs
If 13 people are at a dinner, then at least two of them have the
same birth month.
Equivalence Relations
Counting
Pigeonhole Principle
Proofs
If 13 people are at a dinner, then at least two of them have the
same birth month.
Consider the groups as being “January”, “February”, and so on,
and assign each person to the group of their birth month. Then
there are 13 people assigned to 12 groups, meaning at least two
assigned to the same group.
Equivalence Relations
Counting
Pigeonhole Principle
Proofs
If 51 integers are chosen from the set {1, 2, . . . , 100}, then at
least two are consecutive.
Equivalence Relations
Counting
Pigeonhole Principle
Proofs
If 51 integers are chosen from the set {1, 2, . . . , 100}, then at
least two are consecutive.
Consider the 50 groups
{1, 2}, {3, 4}, . . . , {99, 100}
and assign the 51 chosen integers to the groups. Then two integers
are assigned to the same group, and therefore form a consecutive
pair.
Equivalence Relations
Counting
Pigeonhole Principle
Harder Proof
If 10 integers are chosen randomly from the set {1, 2, . . . , 100}
then the resulting set has at least two disjoint subsets with the
same sum.
Let A be a set of 10 integers chosen from {1, 2, . . . , 100}, and
consider all of the subsets of A.
As A contains 10 elements there are 210 = 1024 subsets.
The smallest possible subset sum is 0, while the largest possible is
100 + 99 + 98 + 97 + 96 + 95 + 94 + 93 + 92 + 91 = 955
Therefore there are at most 956 different subset sums possible.
Equivalence Relations
Counting
Pigeonhole Principle
Proof cont.
Assigning each subset (pigeon) to its subset sum (pigeonhole), it
follows from the pigeonhole principle that there are distinct
subsets, S, T ⊆ A with the same subset sum.
If they are already disjoint then we have found the desired pair of
sets, but if they are not disjoint then let
S 0 = S − (S ∩ T )
T 0 = T − (S ∩ T )
and then S 0 , T 0 are subsets of A with the same subset sum.
Equivalence Relations
Counting
Pigeonhole Principle
Existence Proof
The argument above is known as an existence proof — it provides
a proof that something must exist, but provides no clue as to how
to actually find it.
For example, here is a set that my computer chose “at random”
A = {8, 22, 56, 57, 63, 65, 71, 81, 93, 100}.
Which are the disjoint subsets with the same subset sum?
Equivalence Relations
Counting
Pigeonhole Principle
Existence Proof
The argument above is known as an existence proof — it provides
a proof that something must exist, but provides no clue as to how
to actually find it.
For example, here is a set that my computer chose “at random”
A = {8, 22, 56, 57, 63, 65, 71, 81, 93, 100}.
Which are the disjoint subsets with the same subset sum?
There are many possibilities, but the smallest is {8, 57} and {65}.
Equivalence Relations
Counting
Pigeonhole Principle
More generally
The version of the pigeonhole principle given above is a version of
the more general observation:
Pigeonhole Principle When n items are divided into k groups, then
there is a group containing at least d kn e items and a group
containing at most b kn c items.
(Here dxe denotes the “ceiling function” which is the smallest
integer no smaller than x, while bxc denotes the “floor function”
which is the largest integer no bigger than x.)
Equivalence Relations
Counting
Example
Suppose 10 items are divided into 3 groups.
Then there must be a group containing at least
10
=4
3
items, and there must be a group containing at most
10
=3
3
items.
Pigeonhole Principle
Equivalence Relations
Counting
Pigeonhole Principle
Proof
The average number of items per group is
integer).
n
k
(which may not be an
In any set of numbers, there must be one that is less than or equal
to the average, and one that is greater than or equal to the
average.
So some group has at most
items.
n
k
items and some group has at least
The result follows because each group has an integer number of
items.
n
k