Download Tutorial Questions

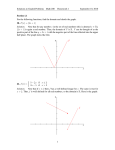
Properties of Matter
Tutorial Questions
Week One
1. In his speech for the Nobel Prize in Physics in 1991, Prof. Pierre-Gilles de Gennes
described a very simple but elegant experiment performed by the American statesman
and amateur scientist, Benjamin Franklin, in the 1700s. See P.G. de Gennes, Reviews of
Modern Physics (1992) 64, 645-648.
Franklin estimated the size of molecules by spreading a layer of molecules on the surface
of a pond on London’s Clapham Common. He used exactly the right volume so that the
surface of the pond was covered by a monolayer of molecules. If the diameter of the
Clapham Common pond is 100 m, and if Franklin spread 25 mL of the molecules,
estimate the length of molecules. (Franklin allegedly spread molecules of oleic acid,
which stand up on end when they are packed in a dense monolayer.) What assumptions
have you made in answering the question?
2. State whether you think each of the following is an open system or a closed system
and explain your reasoning:
(a) water being circulated in pipes in a solar heating system
(b) water in a lake
(c) water vapour in a plastic bottle
3. Some insects can walk on the surface of water. Out of all state variables of the water,
which one is most important in determining whether the insect walks on it?
4. An unknown system is in thermal equilibrium with alcohol contained in a cylinder.
The volume and pressure on the alcohol is found to be the same when it is in thermal
equilibrium with the air in a refrigerator. What can you conclude about the temperature
of the unknown system? Which law of physics supports your conclusion?
Week Two
1. Estimate the number of air molecules in a room (10 m x 6 m x 3 m) at standard
atmospheric pressure and a temperature of 300 K. Assume the room is empty, except for
the air!
2. The density of air inside a hot-air balloon must be 75% of the density of the
surrounding atmosphere to achieve the required buoyancy. If the temperature of the
atmosphere is 10 C, what should be the temperature of the air inside the balloon? You
should assume that the pressure inside the balloon equals the surrounding atmospheric
pressure.
Properties of Matter
Tutorial Questions
Week Three
1. Use the cyclical rule or the chain rule (as appropriate) to find an equivalent expression
for each of the following. Assume that an equation of state exists that is a function of P,
V and T only. Note that the state function called internal energy, U, is a function of P, V
and T.
 P   T 
(a) 
  
 V  T  P V
 U 
(b) 

 T  P
 U   P 
(c) 
  
 P V  T V
1
 T   P   T 
(d) 
 
 

 P V  V T  V  P
2. Starting with an equation-of-state for a one-dimensional system, derive this equation
for the linear expansivity:
1  L 
   ,
L  T 
where T is the temperature,  is the tension, and L is the length of the system.
1  V 

 where V is volume, T is
V  T  P
 P 
temperature, and P is pressure. The bulk modulus K is defined by K  V 
 .
 V  T
3. The volume expansivity  is defined by  
Calculate values of  and K for each of the following:
(a) an ideal gas, with an equation of state PV = nRT, where n is the number of moles of
gas and R is the universal gas constant.
(b) a so-called van der Waals gas, which has a simplified equation of state given as
(P+a)(V-nb) = nRT,
Properties of Matter
Tutorial Questions
where a is a constant related to the pressure change associated with molecular
interactions, and b is a constant related to the volume of the individual molecules.
(c) a certain substance, which has an equation of state given by:
2V – bT3 + aP = c,
where a, b and c are constants, V is volume, T is temperature, and P is pressure.
4. A certain (imaginary) substance has an equation of state given as P 2T 1 / 3 
b
, where
V
b is a constant. Derive an expression for the bulk modulus K of the substance.
Week Four
1. Calculate the work done by one mole of an ideal gas during a quasi-static, isothermal
expansion in which the volume is doubled. How much work is done if the volume is
doubled under constant pressure (i.e. an isobaric process)? Write an expression for the
difference between the work done isothermally and the work done isobarically.
2. 10 moles of an ideal gas are compressed isothermally and reversibly from a pressure
of 1 atmosphere to 10 atmospheres at 300 K. How much work is done on the gas?
3. An ideal gas undergoes the following reversible cycle: (a) an isobaric (i.e. at constant
pressure) expansion from the state (V1, P1) to the state (V2, P1); (b) a reduction in pressure
to P2 at constant volume; (c) an isobaric reduction in volume to the state (V1, P2); and an
increase in pressure at constant volume, back to the original state again. What work is
done in this cycle? If P1 = 3 atm., P2 = 1 atm., V1 = 1 L and V2 = 2 L, how much work is
done by the gas in one cycle?
4. The equation of state for a rubber band is
 L  Lo  2 
  aT      ,
 Lo  L  
where  is the tension on the band, L is its length, Lo is its original length, and a is a
constant equal to 1.3 x 10-2 NK-1. How much work is performed when the band is
stretched isothermally and reversibly from its original length of 10 cm to a final length of
20 cm. The temperature is constant at 20 ºC.
5. (a) The surface tension of a soap bubble surface is 30 mJ m-2. How much work is
done on the bubble when it is expanded from having a radius of 5 cm to a radius of 15
cm. Assume that the surface tension  does not vary with surface area.
(b) Derive an expression for the work done if  depends on area as:  = o exp(A/k),
where o and k are constants.
Properties of Matter
Tutorial Questions
6. Why are soap bubbles usually spherical? To partly answer this question, assume that
a bubble's surroundings cannot perform work on it. If a spherical bubble maintains a
constant volume, can it become cubic under this circumstance?
7. A one-metre length of wire is stretched with a constant tension of 10 kN. If the wire's
thermal expansivity is 5 x 10-6 K-1, how much work is done when the wire is cooled by
20 K? Is the work done on the wire or by the wire?
8. A block of metal at a pressure of one atmosphere is initially at a temperature of 20 ºC.
It is heated reversibly to 32 ºC at constant volume. Calculate the final pressure. The
expansivity  = 5.0 x 10-5 K-1, and the isothermal bulk modulus K = 1.5 x 1011 Nm-2.
9. The pressure on a block of iron weighing 100 g is increased isothermally and very
slowly from 0 to 100 MPa. Calculate the work done on the iron. Assume that the density
is unchanged at 7000 kg m-3 and the bulk modulus is constant and equal to 95 GPa.
10. How much work is done in compressing a van der Waals gas to one-third of its initial
volume under isothermal conditions?
11. Steel rails (with a length of 10 metres) are placed end to end on a rail line with a gap
between each rail of 1 mm at a temperature of 20 ºC. During the heat wave in August of
2003, the temperature reached 35 ºC. The rails each expanded by 1 mm so that they
were placed in compression. What force is placed on the rail lines when they were
heated up? The linear thermal expansivity  of the steel is 8 x 10-5 K-1, and its elastic
modulus Y is 2 x 1011 Nm-2. The cross-section of the rail is 15 cm by 6 cm.
12. How much work is required to break a drop of water of radius 3 mm into smaller
aerosol droplets, each with a radius of 5 m? You can assume that the surface tension of
water is constant as the area is changed and is equal to 0.072 N/m at the temperature of
the process.
Week Five
1. Use the first law of thermodynamics to show that in an isothermal expansion of an
ideal gas the work done by the gas equals the heat absorbed.
2. Explain why in a free adiabatic expansion of an ideal gas from a volume of V1 to a
volume of V2 the temperature of the gas is unchanged.
3. Two moles of a monoatomic ideal gas are at a temperature of 300 K. The gas expands
reversibly and isothermally to twice its original volume. Calculate the work done by the
gas, the heat supplied, and the change in internal energy.
4. Using the first law of thermodynamics, find the change in the internal energy (U) of
one mole of a monoatomic ideal gas in an isobaric expansion at 1 atm from a volume of 5
Properties of Matter
Tutorial Questions
m3 to a volume of 10 m3. Then find U using the definition of Cv. Does your answer
depend on the number of moles of gas?
5. A system is taken from a to b via c, as is shown on the diagram below. On going from
a to b, 80 J of heat flows into the system, and it does 30 J of work on the surroundings.
(a) When the system goes from a to b via d, calculate the amount of heat flowing into the
system if the work done on the surroundings is 10 J.
(b) If the system goes from b to a via the irregular path shown on the diagram when 20 J
of work is done on it, calculate the amount of heat absorbed.
(c) If the internal energy of the system at point a is 0 J and the internal energy at d is 40
J, find the heat absorbed along the paths ad and db.
(Figure copied from Thermal Physics by C.B. Finn.)
6. One mole of a monoatomic ideal gas is at a temperature of 400 K. The gas expands
reversibly and isothermally to three times its original volume. What is the work done by
the gas? How much heat is absorbed by the gas?
Week Six (Heat capacity of gases; degrees of freedom)
1. The tombstone of James Joule is pictured below.
Properties of Matter
Tutorial Questions
Source of image: http://www.findagrave.com/
At the top of the tombstone, the number 772.55 appears. What is the significance of this
number to James Joule (and to physics)?
2. A closed, well-insulated room has dimensions of 10 m x 5 m x 3 m. The room
temperature is 20 C. If a 10-kg copper block at a temperature of 150 C is placed in the
room, what will be the final temperature of the room and block when thermal equilibrium
is reached?
Week Seven
Crystal Structure
1. Sketch each of these directions in a cubic lattice:
(a) [110]
(b) [111]
(c) [321]
2. Sketch each of these planes in a cubic lattice:
(a) (110)
(b) (111)
Properties of Matter
Tutorial Questions
(c) (321)
3. The cesium chloride structure is shown below. The Cl- ions are represented as white
circles, and the cesium ions are represented as black circles. Identify the Bravais lattice
and the basis.
Source: N.W. Ashcroft and N. D. Mermin, Solid State Physics (1976)
4. Potassium chloride (KCl) is known to have an FCC lattice structure. Explain why the
X-ray diffraction pattern of KCl can be misinterpreted as being simple cubic.
Properties of Matter
Tutorial Questions
KCl crystal structure consisting of an FCC Bravais lattice with a basis of K+ (black
circles) and Cl- ions (white circles). Source: N.W. Ashcroft and N. D. Mermin, Solid
State Physics (1976)
Week Eight
1. Derive an expression for the work done by an ideal gas during a reversible adiabatic
expansion from an initial pressure of P1 and volume V1 to final values of P2 and V2.
2. A spherical interstellar cloud, consisting of an ideal gas with  = 5/2, collapses
adiabatically from a radius of 1013 m to a radius of 1012 m. If the initial temperature of
the cloud is 10 K, what is its temperature after its collapse?
3. Given that PV is a constant for a reversible, adiabatic expansion of an ideal gas, show
that TV-1 is also a constant.
4. The fireball of a uranium fission bomb consists of a sphere of gas of radius 15 m and a
temperature of 300,000 K shortly after detonation. Assuming that the expansion is
adiabatic and that the fireball remains spherical, estimate the radius of the fireball when
its temperature is 3000 K. Assume that  = 1.4
5. A spherical interstellar cloud, consisting mainly of helium gas (which is monoatomic),
collapses adiabatically from a radius of 1013 m to a radius of 1012 m. By what factor
does the pressure change in the cloud during the process? You can assume that Cp/Cv =
5/3.
Week Nine
1. Show that for the Carnot cycle shown in the diagram below that the volume ratios in
the two isothermal expansions are the same. That is, show that Vb/Va = Vc/Vd. Hint:
consider what you know about the volume relationship during the two adiabatic
processes.
Properties of Matter
Tutorial Questions
(Figure copied from Thermal Physics by C.B. Finn.)
2. 3 kg of water at a temperature of 0 ºC are in a refrigerator. The room that contains the
refrigerator is maintained at a constant temperature of 21 ºC. What is the minimum
amount of work input into the refrigerator that is required to freeze the water? The latent
heat of fusion for water is 3.33 x 105 J kg-1.
3. You wish to heat your house using a heat pump operating between the house and the
outside. On a typical winter's night, the temperature outside is -5 ºC, and you wish the
temperature inside the house to be at 23 ºC. You estimate that the rate of heat loss from
the house is 20 kW. What is the minimum power required to operate the heat pump?
Week Ten
1. A warm block of lead, weighing 2 kg and at a temperature of 50 C, is tossed into a
cool lake at a temperature of 10 C. The block cools to the temperature of the lake.
(i) What is the entropy change of the block?
(ii) What is the entropy change of the lake?
(iii) What is the entropy change of the thermodynamic universe consisting of the block
and the lake?
You can use the Dulong-Petit law to estimate that the specific heat capacity of lead is
equal to 3R, which is the value approached by solids at high temperatures. The atomic
weight of lead is 207.2 g mol-1.
Properties of Matter
Tutorial Questions
2. Two moles of an ideal gas at T = 400 K expand quasi-statically and isothermally from
an initial volume of 30 L to a final volume of 90 L. What is the entropy change of the
gas as a result of the expansion? What is the entropy change of the thermodynamic
universe?
3. At low temperatures, the molar specific heat of diamond varies with temperature as:
3
T 
c v  1.94  10 3   ,
 
(J mol-1 K-1)
where the Debye temperature, , is 1860 K. What is the entropy change of a 1 mg
diamond crystal when it is heated at constant volume from a temperature of 4 K to 300
K? The atomic weight of carbon (which is the only element that makes up diamond) is
12.01 g mol-1.
4. On the tomb of Ludwig Boltzmann (see below), this equation is written: S = k log W.
What is the physical meaning of this equation? (Incidentally, it was voted one of the top
ten “most beautiful equations of physics” by the readers of Physics World.)
Properties of Matter
Tutorial Questions
Source of image: http://www.findagrave.com/
Week Eleven
1. Show that the difference between the isothermal compressibility (T) and the adiabatic
compressibility (S) is given by:
T  S 
Hint: Make use of what you know about
TV 2
.
CP
T
.
S
2. A block of metal of volume V is subjected to an isothermal reversible increase in
pressure from P1 to P2 at a constant temperature T. Throughout the compression, the
expansivity (), bulk modulus (K) and volume are approximately constant.
(i) Show that the heat given off by the metal is TV(P2-P1).
Properties of Matter
Tutorial Questions
V ( P2  P1 )
(ii) Show that the work done on the metal is given by
2K
2
2
(iii) Using the first law of thermodynamics, and drawing upon parts i and ii, calculate the
change in internal energy (U) of the block.
(iv) Given that internal energy is a function of P and T, U = U(T,P), we can write the
differential dU as
 U 
 U 
dU  
 dT  
 dP
 T  P
 P T
Use this expression to obtain the same result as in part iii. Hint: Make use of one of the
Energy Equations.
(3) Write an expression for an infinitesimal change in temperature, dT, as a function of
changes in pressure, dP, and entropy, dS. Use this expression to solve the following
problem.
A cube of aluminium (2 cm on an edge) at room temperature is adiabatically subjected to
a pressure increase of 1 GPa. What will be its new temperature in relation to its initial
temperature? You can make use of the fact that CP for Al is 24 Jmol-1K-1 (about 3R) and
its volume expansivity () is 3 x 10-6 K-1. The density of Al is 2.7 x 103 kgm-3, and its
atomic weight is 27 gmol-1.
(4) For any system, the heat capacity at constant pressure (CP) and the heat capacity at
constant volume (CV) are related as:
 S   V 
C P  CV  T 
 
 ,
 V T  T  P
where S is entropy and T is absolute temperature. Starting with this equation, show that
CP – CV = nR for an ideal gas, where n is the number of moles and R is the ideal gas
constant.