Download Lecture 1: Crystal structure

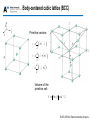
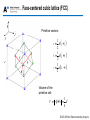
Lecture 1: Crystal structure
OUTLINE
• Crystal binding
• Crystal structures
• Miller indices
ELEC-E3140 Semiconductor physics
• Crystal binding
• Crystal structures
• Miller indices
ELEC-E3140 Semiconductor physics
Crystal binding
• Ionic bond: one electron is transfered from one atom to the other
• Covalent bond: Valence electrons are in common between
neighboring atoms
Na+
ClNa+
ClCl-
ClNa+
C
C
Na+
Cl-
Sodium chloride (ionic)
C
C
C
Diamond (covalent)
ELEC-E3140 Semiconductor physics
Covalent bonds in Silicon
Electronic structure of Si: 1s22s22p63s23p2
4 valence electrons, 4 electrons missing to fill the outer shell
Most electrons involved in the bonds are trapped in the bonds, and
are not available for conduction.
Pure silicon is a poor conductor
But free carriers can be easily created by doping.
ELEC-E3140 Semiconductor physics
Covalent bonds in GaAs
Electronic structure of Ga: 1s22s22p63s2p63d104s24p1
3 valence electrons, 5 electrons missing to fill the outer shell
Electronic structure of As: 1s22s22p63s2p63d104s24p3
5 valence electrons, 3 electrons missing to fill the outer shell
Ga
As
Ga
As
As
Ga
As
Ga
Ga
As
Ga
As
All valence electrons are used to create the covalent bonds
ELEC-E3140 Semiconductor physics
Heteropolar bonds
In semiconductor crystals the bonds are often a mixture of covalent and
ionic bonds
Fractional ionic
character
IV-IV
III-V
Si
0.00
SiC
0.18
Ge
0.00
Fractional ionic
character
II-VI
ZnO
0.62
ZnS
0.62
ZnSe
0.63
ZnTe
0.61
CdO
0.79
InP
0.42
InAs
0.36
InSb
0.32
CdS
0.69
GaAs
0.31
CdSe
0.70
GaSb
0.26
CdTe
0.67
ELEC-E3140 Semiconductor physics
• Crystal binding
• Crystal structures
• Miller indices
ELEC-E3140 Semiconductor physics
Ordering in solid materials
Single crystals
– Atoms are ordered periodically i.e. they form
a lattice
– Translational symmetry, i.e. The crystal
appears identical at several equivalent
regions defined by a basic periodicity
Polycrystals
– Consist of several single crystals ordered
randomly
– Polycrystals are crystalline only locally
ELEC-E3140 Semiconductor physics
Ordering in solid materials
Quasicrystals
– Structure with symmetries but not
translational invariance
Amorphous
– unordered atoms
– No repeating crystal structure can be
found in the material
Quasicrystal pattern
Amorphous SiO2
ELEC-E3140 Semiconductor physics
Ordering in solid materials
Amorphous SiO2 (glass) on top of crystalline silicon
ELEC-E3140 Semiconductor physics
Basic properties of crystal lattices
• Crystal is formed from a lattice (Bravais lattice) and from a basis
consisting of one or more atoms.
• The basis is repeated with the symmetry of the Bravais lattice.
• When travelling from a one lattice point to another, the surrounding
atomic structure is the same (translational symmetry).
• In addition to translational symmetry, the crystal can have rotational,
mirror and inversion symmetries.
ELEC-E3140 Semiconductor physics
Basic properties of 2D crystal lattices
Square lattice
Hexagonal lattice
Areas of crystal that can be repeated to form the full crystal are
called (conventional) unit cells.
The unit cell with the smallest area is called the primitive unit cell.
The vectors defining (spanning) the unit cell are called primitive
vectors.
ELEC-E3140 Semiconductor physics
Examples of 2D crystals
Yksiatominen
One
atom basis kanta
Kaksiatominen
Two atom basis kanta
ELEC-E3140 Semiconductor physics
Primitive vectors
Primitive vectors are not unambiguous – there can be several options (see
red areas above).
All the points in the lattice can be expressed by
R = na 2 + mb 2 ;
n, m = 0, ±1, ±2,..
ELEC-E3140 Semiconductor physics
Wigner-Seitz primitive cell
How to determine the
Wigner-Seitz primitive cell:
• Choose arbitrary atom (or basis)
• Draw lines to neighboring atoms
(or bases)
• Draw the center normal to the line
segment joining atoms (bases)
• The area closest to the chosen
atom (basis) and bounded by the
normals is the Wigner-Seitz
primitive cell
• The Wigner-Seitz cell has the
same symmetry as the crystal
ELEC-E3140 Semiconductor physics
Bravais lattices (2D)
There are five different Bravais lattices in 2D.
ELEC-E3140 Semiconductor physics
Crystal lattice in 3D: unit cell
• Unit cell = a region of a crystal defined by vectors a, b, c and angles
α, β, and γ, which when translated by integral multiples of those
vectors, reproduce a similar region of the crystal.
Parallelopided indicating
The basis vectors and
angles.
• Primitive unit cell = smallest unit cell in volume that can be defined
for a given lattice, i.e. smallest periodically repeated pattern in the
crystal. Most often the primitive vectors are defined as the sides of the
primitive cell
ELEC-E3140 Semiconductor physics
Bravais lattices (3D)
14 lattices in 3D (= Bravais lattices)
The most common semiconductors have a cubic lattice (a=b=c and
α=β=γ=90°)
– SC = Simple Cubic
– BCC = Base Centered Cubic
– FCC = Face Centered Cubic
Simple Cubic
Body-Centered Cubic
Face-Centered Cubic
ELEC-E3140 Semiconductor physics
Bravais lattices (3D)
ELEC-E3140 Semiconductor physics
Simple cubic (SC) lattice
Primitive vectors:
a = dˆi
b = dˆj
c = dkˆ
Volume of the
primitive cell:
V = a×b´c = d3
ELEC-E3140 Semiconductor physics
Body-centered cubic lattice (BCC)
Primitive vectors:
a=
d ˆ ˆ ˆ
(i + j - k )
2
b=
d
2
c=
( -ˆi + ˆj + kˆ )
d ˆ ˆ ˆ
(i - j + k )
2
Volume of the
primitive cell:
V = a´b×c = d / 2
3
ELEC-E3140 Semiconductor physics
Face-centered cubic lattice (FCC)
Primitive vectors:
1
a = d ( i + j)
2
1
b = d (j+k)
2
1
c = d (k + i )
2
Volume of the
primitive cell:
1
V = a ×b´ c = d3
4
ELEC-E3140 Semiconductor physics
Diamond structure
Diamond structure = FCC lattice + 2 identical atoms in the primitive
cell: (0,0,0) and (a/4, a/4, a/4)
– Examples: Si, Ge and diamond
Crystal viewer (diamond and Zinc blende structure):
http://jas2.eng.buffalo.edu/applets/education/solid/unitCell/home.html
ELEC-E3140 Semiconductor physics
Zinc-blende structure
Zinc-blende lattice = FCC lattice + 2 different atoms in the primitive
cell
– Examples: GaAs, InP, GaP, GaSb, InSb, ZnS, ZnSe, …
(GaN, SiC and ZnO are
difficult to manufacture in
zinc-blende structure)
ELEC-E3140 Semiconductor physics
Hexagonal lattice
Simple hexagonal lattice (the blue atoms):
Primitive vectors:
a = a ˆi
b=
(
a ˆ
i+
2
3 ˆj )
c = c kˆ
ELEC-E3140 Semiconductor physics
Hexagonal close packed lattice
Hexagonal close packed structure (HCP)
consists of two simple hexagonal lattices
translated by a vector
a 3+b 3+c 2
ELEC-E3140 Semiconductor physics
Wurtzite structure
Two HCP lattices translated by a
vector (in orange) with different atoms
in each lattice.
Examples: GaN, SiC, ZnO, AlN
ELEC-E3140 Semiconductor physics
Wurtzite and zinc blende structures
Difference between wurtzite and zinc blende structures:
ELEC-E3140 Semiconductor physics
Crystal lattice: parameters
• Lattice constant = the length of a side in a cubic lattice
• Coordination number = the number of nearest neighbor
lattice sites. For example in BCC lattice it’s 8 and in FCC
it’s 12.
• Nearest neighbor distance = distance between
1
neighboring atoms, for FCC it’s 2 a 2
• Packing fraction (assuming spherical atomic shells)=
(volume of each sphere x number of spheres ) / total
volume of the unit cell
ELEC-E3140 Semiconductor physics
Lattice constants
ELEC-E3140 Semiconductor physics
• Crystal binding
• Crystal structures
• Miller indices (next week)
ELEC-E3140 Semiconductor physics