* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Newton`s Second Law of Motion
Specific impulse wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Fictitious force wikipedia , lookup
Atomic theory wikipedia , lookup
Equations of motion wikipedia , lookup
Jerk (physics) wikipedia , lookup
Mass in special relativity wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Electromagnetic mass wikipedia , lookup
Work (physics) wikipedia , lookup
Centripetal force wikipedia , lookup
Classical central-force problem wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Newton's laws of motion wikipedia , lookup
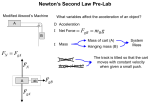
Newton's Second Law of Motion Experimental Objectives: To verify Newton's 2nd law of motion for ar system. This law is r commonly written as Fnet = ma . m is the r total system mass, a represents r its acceleration - - the result of a net force Fnet (the vector sum of all the forces) acting on it. This lab employs an "almost frictionless cart" placed on a ramp (which includes metric markings). The cart is connected over a pulley to a hanging mass as shown in Figure 1 (below). M Track and pulley, "frictionless" cart, various masses, and timer /stopwatch. Apparatus: x Newton's 2nd law is arguably the most important relationship in introductory physics, because it successfully describes how our everyday world works. It is not derived from basic principles, but stands on its own as a fundamental relationship between force, mass and acceleration. r r Rewriting it as a = Fnet m , one can see that this law predicts that a system's acceleration is inversely related to its mass if the net force acting on it is constant. More mass, less acceleration. if the mass is r Instead, r constant, then Fnet ∝ a . That is, the system's acceleration should be directly proportional to the net force acting on it. More net force, more acceleration. Fundamentals: x Figure 1: Car, Ramp and Hanging Mass Note the ramp is tilted downward. This compensates for the friction present. Before starting, remove the hanging mass and adjust the ramp angle so the cart alone (mass M) moves downward at constant speed, determined by eyeball. This in effect makes the cart "frictionless" and the net force is due only to the gravitational force on the hanging mass, m. Thus the net force on the system is Fnet = mg . Express the mass in kilograms and recall that g = 9.80 m s2 to ensure the net force is in newtons. During any one run, the forces on our system will be constant, therefore the net force and acceleration will be constant. Thus our constant acceleration equations are applicable. The most useful one for this laboratory is the one that relates location to Procedure for Constant Mass: 1. Here you will keep the mass of the system constant and vary the net force. First add a 500 g block to the cart. Then place six 5.0 g masses and the paper clip on the cart. Measure the total mass. (It should a bit more than 1 kg). acceleration, that is: x = xo + vot + at 2 2 . Our system will start at rest and we choose the initial location to be the origin. Thus the displacement is given by x = at 2 2 or, solving for acceleration: a = 2x t 2 m floor (1) (over) Hence by measuring the time t it takes for a system to move a distance x we can compute its acceleration. Apparatus and Preliminaries: 1 Starting from rest, let the cart roll a distance x, (perhaps 60 to 80 cm) making sure the dangling mass does not hit the floor. Measure the roll time t. Now add one 200 g slotted mass to the cart, calculating the total system mass (in kg). Repeat this four more times, each time adding an additional 200 g slotted mass to the cart. Arrange your data in column form with the following suggested column headings: Mtotal, x, t, a (calculated from Eq. 1) and 1/a. Be sure to include units. Your instructor will tell you if the data should be displayed on paper or in a computer spreadsheet such as EXCEL. Constant Mass (continued): 2. Now move one of the 5.0 g masses to the paper clip holder. Determine the mass of the paper clip and combine the two to get the dangling mass m (in kg). Starting from rest, let the cart roll a distance x, (perhaps 60 to 80 cm) making sure the dangling mass does not hit the floor. Measure the roll time t. Repeat this five more times, each time moving another 5.0 g mass to the paper clip holder. Arrange your data in column form with the following suggested column headings: m, Fnet, x, t, and a (calculated from Eq. 1). Be sure to include units. Your instructor will tell you if the data should be displayed on paper or in a computer spreadsheet such as EXCEL. Verifying the 2nd Law [constant Fnet]: 1. Graph the total system mass (in kg) on the vertical axis and the inverse of the acceleration (1/a in s2/m) on the horizontal axis. Your graph may be done on paper or on the computer, depending on how you were told to accumulate the data. Regardless, Newton's second law predicts that this should be a straight line. Is yours? Comment. Verifying the 2nd Law [Constant Mass]: 1. Graph the net force on the vertical axis and the acceleration on the horizontal axis. Your graph may be done on paper or on the computer, depending on how you were told to accumulate the data. Regardless, Newton's second law predicts that this should be a straight line. Is yours? Comment. 2. Either by eyeball slope-intercept method or using computer software, determine the equation of the line. Since we expect 1 M total = (Fnet ) , if the net force is a constant, this is of the form Y = AX where A = constant = Fnet . Thus not only should the data plot as a straight line, but the slope should equal the net force on the system. Are they in agreement (to within 10%)? Comment. 2. Now either by eyeball slope-intercept method or using computer software, determine the equation of the line. Since we expect Fnet = M total a , with the total mass constant, this is of the form Y = AX where A = constant = M total . Thus not only should the data plot as a straight line, but the slope should equal the total system mass. Are they in agreement (to within 10%)? Comment. (next page) Procedure for Constant Net Force: 1. Here you keep the net force on the system (mg) constant and vary the total mass (M+m) by changing the cart's mass. A convenient value for the dangling mass is 30 g. Be sure to add the paper clip mass to determine the value of m. (Your instructor may or may not require some or all of these). Follow-Up Questions: A. 2. Remove the 500 g block that was on the cart. Measure the mass of the cart itself. 2 To start the experiment the ramp was tilted downward until the cart rolled at constant velocity - - the cart was not accelerating. For this situation, draw the free body diagram of the forces on the cart. Use it to explain how the forces canceled out. B. To start the experiment you tilted the ramp downward until the cart rolled at constant velocity. Suppose the required angle was 2.0o. Use this to estimate the force of rolling friction on your cart. (HINT: Draw the free body diagram of the cart, or see Follow-Up Question A. You will also need the mass of the cart.) C. For the constant mass section of this experiment, how would your graph change, if at all, if you had not placed the additional 500 g mass in the cart at the beginning? Explain. D. For the constant net force experiment, how would your graph change, if at all, if you had not removed the 500 g mass before you started. Explain. E. Using the constant mass data with the largest dangling mass used, to predict the roll time measured if the roll distance was 20 cm. Show your work. F. Using the constant net force data to predict the roll time measured if the roll distance was 40 cm and the cart had 300 g extra on it. Show your work. G. Suppose you had a horizontal ramp and a cart with a mass of 1.00 kg, connected to a 50 g mass dangling over a pulley. If the force of rolling friction were 5.0% of the normal force on the cart, use Newton's 2nd law and the cart's free body diagram to determine the cart's acceleration. [Rev. 6/07] 3