Download 1025 Sec. 2.1 Notes

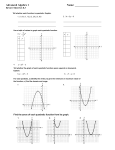
Math 1025: Elementary Calculus
Ch. 2 Nonlinear Functions & Models
Sec. 2.1: Quadratic Functions & Models
I.
Quadratic Functions
x is a function that can be written in the
2
form f (x) = ax + bx + c (function form) or y = ax + bx + c (equation form) where a,b,c
are real numbers, a ≠ 0 .
A. Definition: A quadratic function of the variable
2
B. Graph of Quadratic Functions
f (x) = ax 2 + bx + c, a ≠ 0 is a parabola.
a. The graph opens upward (concave up) if a > 0
1. The graph of
a<0
b. The graph opens downward (concave down) if
2. Vertex of a parabola:
a. The vertex is the maximum or minimum point of the parabola.
b. Coordinates:
⎛ −b ⎛ −b ⎞ ⎞
⎜⎝ 2a , f ⎜⎝ 2a ⎟⎠ ⎟⎠
y
3. Intercepts
a.
y-intercept: Occurs when x = 0, i.e., f (0) = c
x
b.
x-intercept(s): Occur when f (x) = 0
1) In order to find the x-intercepts, solve ax
x=
quadratic formula,
2
+ bx + c = 0 by factoring or using
−b ± b 2 − 4ac
2a
2) Number of x-intercepts:
b 2 − 4ac , to determine the number of x-intercepts
2
2
2
a) Two: b − 4ac > 0
b) One: b − 4ac = 0
c) None: b − 4ac < 0
Use the discriminant,
y
y
y
x
x
x
4. Symmetry:
The graph of
x=
f (x) = ax 2 + bx + c is symmetric with respect to the vertical line,
−b
, that passes through the vertex.
2a
y
x
C. Examples
1. Example 1:
f (x) = x 2 + 6x + 5
a. Does the graph open upward or downward?
b. Determine the vertex.
c. Determine the axis of symmetry.
d. Determine the y-intercept.
e. Determine the
f.
Graph
x-intercept(s), if any.
f (x) = x 2 + 6x + 5
y
5
x
y = x 2 + 6x + 5
4
3
2
1
-5 -4 -3 -2 -1
-1
-2
-3
-4
-5
1
2
3
4
5
x
2. Example 2: A projectile is fired straight up from a 4 foot platform with an initial speed
of 160 feet per second, then its height above ground can be modeled by
s(t) = −16t 2 +160t + 4 where t is measured in seconds and s(t) is measured in feet.
a. Evaluate s(8) and interpret.
b. Determine the maximum height of the projectile.
c. When did it hit the ground?