Download Section 3.2a - Solving Quadratic Equations by Factoring

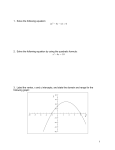
MAC 1105 Section 3.2a – Solving Quadratic Equations by Factoring
A quadratic equation – one that contains an x2 term – can be solved by setting the equation = 0,
factoring, then setting EACH factor = 0, and solving the new equation(s). When factoring,
remember to ask yourself:
A. Can I take anything out?
1. 5x2 – 6x = 0
2. 7x2 – 21x = 0
B. Is it the difference of two squares?
3. 4x2 – 25 = 0
4. 144x2 – 49 = 0
C. Is it a trinomial?
5. x2 - 7x - 8 = 0
6. x2 +12x – 36 = 0
7. 2x2 + 11x – 6 = 0
D. Have I factored completely?
8. x3 - 6x2 - 27x = 0
9. –2x2 + 32 = 0
E. If the equation if not "=0" you must FIRST simplify and get 0 on one side, with the
polynomial in descending order. Remember to get rid of parentheses and denominators
before adding or subtracting.
10. 6x - 27 = 3x2 - 12x
11.
2 2
x  x  2x  3
3
F. Shortcut for binomials – isolate the x2 term and square root both sides. Remember to
use 
12. x2 – 7 = 0
13. 9x2 – 11 = 0
G. Applications: In graphing quadratic functions it is helpful to identify both the vertex AND the xintercepts. To find the x-intercepts of any function we substitute 0 for y and solve for x.
 b
 b 
Determine the vertex   , f     and x-intercepts of the following quadratic functions, and
 2a  2a  
sketch the graphs.
1. f(x) = -3x2 + 12
2. f(x) = 3x(x – 4) – 15
Homework: Problems 1 – 7, 13, 21, and part c only of problems 31, 33, 35, 45, 47, 53
In addition, work the following two problems:
Determine the vertex and x-intercepts and sketch the graph (no calculators):
1. f(x) = x2 + 4x – 32
2. f(x) = -2x2 + 18
Selected Answers: 2) 3, 6 4) 0, 7
6) -7, -1/4
Worksheet answers: 1) V = (-2, -36) Int: -8 and 4
2) V = (0, 18) Int: 3 and -3
054