Download Radical Expressions and Graphs

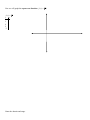
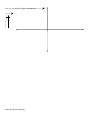
Radical Expressions and Graphs
Definition: In the expression n a the a is the radicand and n is the root index and the entire expression
radical.
For example: In 49 the radicand is 49 and the root index is 2.
Example 1: Simplify with your calculator.
a) 3 64
b)
4
256
c)
5
243
49 =
Why? __________________________________________________.
36 =
Why? __________________________________________________.
In general,
n
a  b because b n  a .
3
8  2 because 23  8
3
8  2 because (-2)3  8
n
a is a
Example 2: Fill in the blank.
a)
5
32  2
because ______________________________________.
b) Plug this into your calculator:
3
6859  ______ because ________________________________.
c) Plug this into your calculator:
5
59049 = _____ because _______________________________.
d) Because radicals are often irrational numbers, the book will round those answers to three decimal
places. Find 4 6825 rounded to three decimal places.__________________.
Definition:
1) If the index (n) is even and the radicand (a) is positive or 0 like in
n
a represents the principle nth root of a.
49 ,
0 , 4 16 , or
6
64 , then
49
0
4
16
6
64
 n a represents the negative nth root of (a) like in:
 49
 0
 4 16
 6 64
2) If the index (n) is even and (a) is negative then
n
a is not real like
36 or
4
16 is not real. Why?
3) If the index (n) is odd then there is exactly one nth root of (a) which is n a , for example:
3
8
3
8 
5
 32 
Example 3: Simplify.
a)  36
b)
5
243
c)
25
d)
4
256
Now we will graph the square root function ( f ( x)  x ).
f ( x)  x
x
y
0
1
4
9
-1
Name the domain and range.
Now we will graph the cube root function ( f ( x)  3 x ).
f ( x)  3 x
x
y
-8
-1
0
1
8
Name the domain and range.
What if the root index (n) is the same number as the powers the radicand is raised to?
These problems may look like
(n) values.
32 ,
1) If n is an even positive integer,
n
6
(3)6 , or
3
(2)3 . We are going to look at these with even and then odd
an  a .
32 
(3)2 
6
(3)6 
6
(3)6 
4
x4 
So again, if n is an even positive integer,
n
an  a .
2) If n is an odd positive integer,
3
(2)3 
3
(2)3 
5
5
3
n
an  a .
(4)5 
(4)5 
x3 
So again, if n is an odd positive integer,
n
an  a .
A word of comfort: Yes this is confusing but the only time we will need absolute value is when the radicand is a
variable and of course the root index is even. When it does occur, the directions will generally say assume all
variables represent positive real number so you won’t have to worry about absolute value.
3
x3  x
4
x4  x
Example 4: Simplify each root:
a)
4
(5)4
d)  4 m4
b)
5
(5)5
e)  x2
c)  6 (3)6
f)  3 x3